INTRODUCTION
A pervasive theme in contemporary language research is that frequency matters. In language acquisition, this point is amply established for a variety of domains (word-learning: Goodman, Dale & Li, Reference Goodman, Dale and Li2008; Graf Estes, Evans, Alibali & Saffran, Reference Graf Estes, Evans, Alibali and Saffran2007; Vosoughi, Roy, Frank & Roy, Reference Vosoughi, Roy, Frank, Roy, Ohlsson and Catrambone2010; phonotactics: Jusczyk, Friederici, Wessels, Svenkerud & Jusczyk, Reference Jusczyk, Friederici, Wessels, Svenkerud and Jusczyk1993; Mattys & Jusczyk, Reference Mattys and Jusczyk2001; phonetic categorization, perception: Anderson, Morgan & White, Reference Anderson, Morgan and White2003; production: Beckman, Yoneyama & Edwards, Reference Beckman, Yoneyama and Edwards2003). It has become clear that to properly validate our theories, we must have a detailed understanding of the input, including the frequency relations it contains.
This article focuses on the frequency of consonantal manner-of-articulation classes (stop, liquid, nasal, etc.) in English. More specifically, it focuses on variation in input frequencies: (i) How much variation is there? (ii) What contributes to it? and (iii) How much does it matter for language acquisition, if at all? In brief, this article will argue that the answers to these questions are: (i) a great deal more than might have been expected; (ii) the sparse/bursty distribution of words across different conversations and topics; and (iii) it doesn't matter much for the child, but it matters a great deal for researchers. Even if the empirical focus is rather narrow, it is to be hoped that the article is of general interest, since the methodological points of this study are likely to generalize to other domains. For example, the finding that segments have a ‘bursty’ distribution (see below for further exposition) complements existing research showing that words are bursty, and suggests that many other linguistic structures of interest, such as particular syntactic constructions, are also bursty.
The role of frequency in segmental acquisition
One reason to focus on variation in segmental frequencies is that absolute segmental frequency appears to matter for segmental acquisition. For example, coronal obstruents are more frequent than dorsal obstruents in English, and English-learning infants exhibit reduced discrimination of a non-native coronal contrast earlier than for a non-native dorsal contrast (Anderson et al., Reference Anderson, Morgan and White2003), which may be interpreted as more rapid acquisition of the native coronal category (Werker & Tees, Reference Werker and Tees1984). Analogously, Beckman et al. (Reference Beckman, Yoneyama and Edwards2003) showed that in Japanese, dorsal stops were more frequent than coronal stops, and Japanese-learning children produced dorsal stops more rapidly and/or more accurately than coronal stops, while English-learning children exhibited the opposite pattern. In short, the place of articulation that was more frequent in the input was acquired faster.
It is natural to ask whether this general pattern also applies to other articulatory dimensions of contrast. Manner of articulation is an especially important phonological dimension, since manner is correlated with sonority and syllabification. To my knowledge, very few studies have directly investigated frequency of manner-of-articulation classes in the input. One study that has was Lee and Davis (Reference Lee and Davis2010); it is described here in more detail because the results and their interpretation bear closely on the present study.
Lee and Davis conducted a series of laboratory play sessions in English and Korean in which toys were introduced to mother–child and mother–experimenter dyads (only the English data will be considered here). Sampling the 250 syllables of mother speech after the introduction of each of four toys (2010: 773), the experimenters analyzed various segmental frequency distributions and found significant differences on every dimension investigated (p. 775). For example, they found that nasals were more frequent in the mothers' speech to the experimenter than to their infants. Lee and Davis interpreted their results as showing that “English ADS and IDS show different consonant and vowel distribution frequencies” (p. 788; IDS = ‘infant-directed speech’; ADS = ‘adult-directed speech’). That is, they suggest that adult input and child input are two distinct varieties of English, because the statistical differences they found in their samples reflect differences between these two varieties as a whole. In fact, Lee and Davis go further by proposing that the differences they observed reflect some kind of tailoring by caregivers: “These results for consonants and vowels in IDS and ADS suggest that caregivers are sensitive to their infants' developmental stage of segmental production mastery and adjust their IDS to the level of infant production capacities” (p. 785).
Lee and Davis' (Reference Lee and Davis2010) study addresses questions of broad theoretical interest: (a) Is the input to the child different from the input to adults? (b) If so, what causes the difference? The present study will offer a different perspective on these questions than the one offered by Lee and Davis; a theme of this article will be that aspects of the sampling and analysis process may dramatically affect the nature of the results a researcher obtains.
As a starting point, it may be observed that Lee and Davis affected the topic of conversation in their study by sampling directly after the introduction of a limited set of novel toys. They explicitly indicated that many of the segmental differences they found derived from lexical items that were associated with the target toys (2010: 779–83, 785–87). From this fact, it is evident that the IDS and ADS samples that they collected are not representative of IDS and ADS as a whole (since infant and adult conversations do not all share the property that they took place immediately after the introduction of these same toys). Since many of the manner-class frequency differences they found were driven specifically by toy-associated lexical items, there is no reason to expect that these differences would generalize from their samples.
In fact, there is a deeper theoretical reason to doubt the claim that caregivers tailor the segmental frequency distribution of their speech so as to scaffold child language development. While it is robustly and cross-linguistically documented that adults tailor aspects of their speech for infants/children (de Boer & Kuhl, Reference de Boer and Kuhl2003; Casagrande, Reference Casagrande1948; Cooper & Aslin, Reference Cooper and Aslin1990; Goldowsky & Newport, Reference Goldowsky, Newport and Mead1993; Kuhl et al., Reference Kuhl, Andruski, Chistovich, Chistovich, Kozhevnikova, Ryskina, Stolyarova, Sundberg and Lacerda1997; Morgan & Demuth, Reference Morgan and Demuth1996; Snow & Ferguson, Reference Snow and Ferguson1977; but see Englund & Behne, Reference Englund and Behne2006; Kirchoff & Schimmel, 2005; Lam & Kitamura, Reference Lam and Kitamura2010), there is little evidence that manipulating the segmental content of an utterance is a natural stylistic alteration for speakers. For example, it is arguably a universal aspect of communicative competence to exaggerate the pitch range when in a noisy environment or speaking to children, but it seems a priori unlikely that caregivers would know how to implement a strategy like ‘avoid nasals’. Given the theoretical interest of the questions raised by Lee and Davis (Reference Lee and Davis2010), it seems wise to seek additional evidence bearing on them.
It is argued here that the null hypothesis should be that adult and child input do not differ in segment class frequencies. Rather than consider all imaginable classes of segments, the present article focuses on consonantal manner classes to achieve greater empirical coherence; the general findings about variability in segmental frequency distributions presumably generalize straightforwardly to other classes, such as vowel height and consonant place. The prediction that child and adult speech do not differ on this dimension derives from the bedrock linguistic principle of the arbitrary relationship of the signifier to the signified (Saussure, Reference Saussure1922). It seems clear that adults will use some words more often when they speak to children than to adults (e.g. you, zebra), and other words more often when they speak to adults than to children (e.g. however, economy), and that these differences originate in the meanings that adults wish to discuss with children versus adults. If the relationship between the signifier and the signified is truly arbitrary, then it should be the case that meaning-level properties (such as what dictate the relative interest to children versus adults) are independent of form-level properties (such as whether a word contains a nasal). This article adopts the position that this independence may be interpreted in a statistical sense; this intuition forms the mathematical basis for the formal definition of ‘the null hypothesis’ given in the next section.
Prior to this, it must be acknowledged that language acquisition is unique in offering up so many exceptions to the arbitrariness of form–meaning relationships. For example, the cross-linguistic prevalence of /mama/, /papa/, and /dada/ as family nicknames plausibly derives from the early articulatory capabilities of infants. Other notable studies in which phonological factors affect the acquisition of word meanings may be found in Stager and Werker (Reference Stager and Werker1997) and Imai, Kita, Nagumo and Okada (Reference Imai, Kita, Nagumo and Okada2008). Thus, while the relation between form and meaning is not always completely arbitrary, the principle is so robustly established that it should be assumed until there is evidence to the contrary. Indeed, this is the usual basis for defining a null hypothesis.
Terminology
The input
For the purposes of this article, ‘the input’ is defined as the set of utterances a listener hears that were not produced by that listener. For methodological and theoretical reasons, the present study does not distinguish between input that was directed to the listener and other input.
Language variety
A language variety is a set of utterances that share properties of interest. In the present article, the relevant property is whether the target listener is a child or an adult. Note that the terms ADS/IDS/CDS are avoided here, since it was infeasible (and arguably undesirable) to eliminate utterances from the input that were not directed toward the listener. (However, the majority of child input utterances in the present study were likely to be child-directed; see the ‘Corpora’ section for more details).
Document/sample
Informally, a sample of speech refers to a collection of utterances that were uttered together in temporal succession, for example a 15-minute conversation between two people. This study uses the CHILDES (MacWhinney, Reference MacWhinney2000) and Buckeye (Pitt, Johnson, Hume, Kiesling & Raymond, Reference Pitt, Johnson, Hume, Kiesling and Raymond2005) corpora to select samples representing child and adult input, respectively. Like most corpora, these corpora are composed of multiple files, each representing a sample of speech. In this article, ‘document’ will be used to refer to the contents of one such file after preprocessing. The goal of preprocessing was to isolate the phonological input to a single listener. ‘Sample’ will be used interchangeably with ‘document’.
Relative frequency
The relative frequency Pr(x) of an item x is the absolute frequency of the item Fr(x), divided by the total frequency F of all items in a comparison set X, Pr(x) = Fr(x)/F, F = ∑y∊X Fr(y). In this article, the items and comparison set will be segments (Experiment I) or consonantal manner classes (Experiment II) unless explicitly noted otherwise.
Characterizing linguistic frequency distributions
A phrase like “the probability of [l] is 0·035” evokes a mental model known technically as a stationary, ergodic process. The canonical example of a stationary, ergodic process is coin flipping. Stationary means that the probability of events is constant, rather than varying with time. For example, we normally believe that a coin does not become biased toward heads over time. Ergodic means that all sources are equivalent, i.e. the statistical properties are the same whether one obtains samples by flipping one coin 100 times, ten coins ten times, or 100 coins one time each. It is no understatement to say that the assumptions of stationarity and ergodicity underpin much of the probabilistic reasoning in contemporary science. For example, nearly all parametric statistical tests commonly used in the social sciences, such as the t-test and ANOVA, assume that samples are drawn from a stationary, ergodic process. Some readers may be more familiar with the equivalent phrasing that samples are independently and identically distributed.
In the case of language, the most well-known case of a stationary, ergodic process is the bag-of-words model. This is a statistical model in which the occurrence of a word is treated as if it were generated by reaching one's hand down into a giant bag containing millions of word tokens, and drawing one out at a time (and putting each word back after it was drawn, to keep the probabilities constant across draws). This type of model is also known as a word unigram model – ‘word’ because the event of interest is the occurrence of a word, and ‘unigram’ meaning that the likelihood of a word is estimated purely from that word's frequency (rather than conditioning on additional information, such as identity of the preceding word and/or facets of the syntactic structure). In the present case, the linguistic level of interest is the segment, rather than the word. It is a simple matter to define a bag-of-segments model by analogy – there is a fixed probability μ(ϕ) for each manner class ϕ, and the probability of a document δi containing the sequence [ϕ1ϕ2..ϕn] is the product of the probabilities of each element, Pr(δi) = Πj = 1..n μ(ϕj).
The null hypothesis
‘The null hypothesis’ is that the segmental frequency distribution of a language (here, English) is unigram and unitary. The distribution of a language variety is unigram if it can be modeled as a stationary, ergodic process. The distribution of a language is unitary if it can be modeled as a single language variety. Thus, the null hypothesis is that English may be modeled as a single language variety that is generated by a stationary, ergodic process. (A salient alternative hypothesis is that English segmental frequencies must be modeled as consisting of at least two distinct language varieties, i.e. one for child input and another for adult input.) Note that these are two independent properties. It is logically imaginable that a language would consist of distinct varieties, each of which was unigram; it is also logically imaginable that a language might consist of a single variety that is not unigram. In fact, this article will argue that this latter is the most insightful characterization of the true state of affairs for English segmental frequency distributions.
Rationale for the null hypothesis
Before investigating in detail, it may be worth reviewing why this is a good null hypothesis. Many probabilistic language models treat language production as a stationary, ergodic process, and this idealization has been applied in a wide variety of research. Uses include speech technologies like machine translation and automatic speech recognition (Jurafsky & Martin, Reference Jurafsky and Martin2009), predicting adult behavior in psycholinguistic experiments (e.g. Norris & McQueen, Reference Norris and McQueen2008), unsupervised approaches to word segmentation (Daland & Pierrehumbert, Reference Daland and Pierrehumbert2011; Goldwater, Griffiths & Johnson, Reference Goldwater, Griffiths and Johnson2009), phonetic category learning (Dillon, Dunbar & Idsardi, to appear; Feldman, Griffiths & Morgan, Reference Feldman, Griffiths, Morgan, Taatgen and van Rijn2009), and modeling syntactic change (Niyogi, Reference Niyogi2006; Pearl & Weinberg, Reference Pearl and Weinberg2007). Of course, everyone recognizes that language is not actually a giant coin flip – but it is an unusually convenient assumption mathematically, and the record suggests it has also been a highly useful one. In other words, the stationary, ergodic assumption makes for a wonderful null hypothesis; the relevant research question is when it matters that the null hypothesis is incorrect.
A known failing of the null hypothesis: burstiness
It is well known that once a word has occurred in a document, the likelihood of it occurring again (and again) is far greater than expected under stationarity (Baayen, Reference Baayen2001), a property that may be referred to as burstiness. When this occurs, it follows from the axioms of probability that the likelihood of one or more other words must decrease correspondingly; in other words, word probabilities are not actually stationary. Presumably, this kind of non-stationarity arises from multiple factors, including authors' preferences for particular words, as well as the fact that documents are about one or more topics, and words are more likely to recur if they are associated with the same topic.
Burstiness is such a significant property of language that it plays a role in corpus design for frequency estimation. A humorous example comes from Serge Sharoff's comment on the frequency list he derived from the Russian National Corpus (http://www.artint.ru/projects/frqlist/frqlist-en.php):
As an example, the corpus contains a huge sequel to Tolkien's The Lord of the Rings written by a Russian author (Nick Perumov). In spite of the fact that the length of the sequel is about 250 kW, less than one percent of the whole corpus, the frequency of uses of the word hobbit in that book puts the word in the first thousand of most frequent Russian words, if no precautions against large texts are made.
A related case, albeit not strictly in the same category as online speech production, comes from baby names. As documented by Levitt and Dubner (Reference Levitt and Dubner2005), using American census data, baby names exhibit a bursty frequency distribution (i.e. naming fads). Specifically, they show that some names (e.g. John) show a relatively stable frequency across all decades for which data is available, while other names (e.g. Kayla) undergo a rapid rise and an equally rapid fall in popularity. Similar points hold for mention of topical entities and concepts, for example as illustrated by the frequency of the lexical item sustainability over time (http://xkcd.com/1007/).
A recent study (Altmann, Pierrehumbert & Motter, Reference Altmann, Pierrehumbert and Motter2009) investigated the distribution of intervals between successive occurrences of the same word in the USENET corpus (a precursor to the modern Internet, consisting of fora on a wide variety of topics). The null hypothesis – in that article, a bag-of-words model – would predict an exponential distribution in co-occurrence intervals (that is, the distribution over intervals, measured in number of words, between successive occurrences of the same word). However, what Altmann and colleagues actually found was a Weibull distribution (also described as a ‘stretched exponential’, see their article for exposition and additional technical details, such as rescaling to compare across different basal frequencies). This means that, similar to baby names, most words will be under-represented in some samples (relative to their expected rate of mention under stationarity), and then in others be comparatively over-represented. Just as different names exhibit differing degrees of faddiness, the authors found that words vary considerably in the extent of burstiness. Going beyond the works mentioned above, they proposed to measure a word's level of burstiness parametrically by quantifying the degree of deviation from the null hypothesis. Using this measure, they showed that words which serve core, syntactically obligatory functions in English, like the and to, deviated the least from the null hypothesis (although they are still modestly bursty), while words that were highly associated with specific topics (like evolution and Eminem) were the most bursty.
Follow-up studies showed that participants are sensitive to burstiness in perception and production: controlling for frequency, bursty words exhibit larger changes in word duration between first and second mention (Heller & Pierrehumbert, Reference Heller and Pierrehumbert2011) as well as larger changes in eye fixations in a self-paced reading task (Heller, Pierrehumbert & Rapp, Reference Heller, Pierrehumbert and Rapp2010). These effects imply that listeners dynamically adjust their expectations of upcoming linguistic material in a way that cannot be explained by the null hypothesis.
In summary, it seems to be an inherent property of words that they are more or less bursty. Burstiness appears to be associated with topicality, in the sense that words which deviate the most from the null hypothesis also tend to be strongly associated with particular topics. Words that deviate the least from the null hypothesis tend to subserve topic-general, core functions of English such as syntactically obligatory marking. Even within the same class of words, some words are more bursty (e.g. Obama), and others less so (e.g. John). Burstiness is a general property of word systems (e.g. baby names), so it is not specific to on-line speech perception/production; nonetheless speaker–listeners know that words are bursty and adjust their productions/expectations dynamically on the basis of burstiness. Burstiness effects are one important case that cannot be modeled by the null hypothesis. Even though the null hypothesis does not predict burstiness or its effects, it has proven an excellent statistical model of language, useful in pure and applied research across a variety of linguistic domains.
The statistical signatures of bursty processes
In a stationary, ergodic process with a finite number of outcomes per trial, each outcome ϕ will have some constant probability μϕ of occurrence. In a sequence of n trials, the number of occurrences of ϕ will be a binomially distributed random variable whose expected value is nμϕ and whose variance is nμϕ(1 − μϕ). Therefore, the expected relative frequency is μϕ and the predicted variance about this value is μϕ(1 − μϕ). One way to evaluate whether a distribution is stationary and ergodic is to determine whether the actual variance around the mean is as predicted. If there is greater variation than predicted, the distribution must not be stationary and ergodic. Rather, the item(s) in question must be systematically over-represented in some documents, and systematically under-represented in other documents, relative to the variation that is expected. (It is also logically possible that the variance is less than predicted. This would occur in rhythmic distributions, for example, if an item recurred exactly once every fifty trials.)
When an item is more frequent in one document, and less frequent in another, it follows mathematically that the average interval between occurrences must be shorter in the former, and longer in the latter. On analogy with the all-or-nothing firing patterns of neurons, it is said that the item is ‘bursting’ in the former case, and ‘lulling’ in the latter case. Thus, an alternative way to assess burstiness is to measure the co-occurrence interval distribution; this is the method used by Altmann and colleagues. This article assesses burstiness using the relative frequency counts method, rather than the co-occurrence interval method. The primary rationale is that it is simpler to collect relative frequency distributions than co-occurrence interval distributions; arguably it is also simpler to avoid explicating certain mathematical aspects of the Altmann et al. (Reference Altmann, Pierrehumbert and Motter2009) study in the present case.
CORPORA
Having described the null hypothesis in some detail, the article turns now to the data which forms the empirical basis for this study – adult- and child-directed corpora from which ‘the input’ samples were extracted. In addition, a ‘social summary’ of the CHILDES (child-directed) corpus is given, including summary statistics as to how much speech was produced by various participant types. This was done for two reasons: first, to get reasonable bounds as to what percentage of the input analyzed here is child-directed; second, because it is of general intellectual interest to analyze the social make-up of the input to children.
The general process by which child and adult input samples were obtained consists of several steps. First, raw corpus files were downloaded from the corpora repositories. Next, they were preprocessed to yield input files, consisting of input utterances. Then, input files were converted to phone files by looking up the phonological form of words in a dictionary; the resulting phone files yielded a phonological representation of the input in the original corpus files. Finally, segmental frequencies were tallied for each file, and the database of tallies was used in the experiments.
This process was done separately for the Buckeye/adult corpus and the CHILDES/child corpus. The description focuses mainly on the child input, which came from a more heterogeneous corpus; the process for the adult corpus was analogous, though more straightforward.
The CHILDES corpus
The CHILDES project was one of the first crowd-sourcing projects applied to linguistic data. Brian MacWhinney solicited other child language researchers to share the transcriptions they had collected in the course of their research. In the course of the project, the CHAT coding conventions were established, and to the extent that it was feasible, corpora were adjusted to conform to those conventions. As the original subcorpora comprising the corpus were collected by a variety of researchers working with children of varying ages and for varying purposes, the corpus is extremely heterogeneous. Further description is omitted, as readers of this journal are likely to be familiar with CHILDES.
The Buckeye corpus
The Buckeye corpus was collected with the intention of collecting a representative sample of the variation in speech from native talkers of a typical Midwestern town. Forty age- and gender-stratified (3 age groups, male and female) lifelong residents of Columbus, Ohio were recruited and recorded having an informal discussion with a researcher. The topic of conversation varied within and across talkers, and generally concerned local events of interest, such as sports and politics. For each speaker, two or three segments of a few minutes' duration each were chosen for transcription. Each segment was orthographically transcribed, and then phonetically transcribed using a semi-supervised process with two iterations; this is the unit that ‘document’ refers to for the adult input. This article used the orthographic transcripts. It should be noted that the Buckeye corpus is considerably less heterogeneous than the CHILDES corpus; in comparison to the remarkable diversity of social situations sampled in CHILDES, every document in the Buckeye consists of a talker speaking one-on-one with a researcher. The reader is referred to Pitt et al. (Reference Pitt, Johnson, Hume, Kiesling and Raymond2005) for further details.
Preprocessing I: isolating the input
In the Buckeye, a sample is made up of several files. For each sample, there is exactly one file with the extension.txt; this file is a close orthographic transcription of the speaker's speech. Interviewer speech, vocal noises, and incomplete words were all treated as utterance boundaries; otherwise contiguous sequences of words were copied directly to the input file using a custom Python script (run from the Windows 2007 IDLE Python 2.7.2 shell and/or a Cygwin terminal shell on the same OS).
In the CHILDES files used here, a sample consists of an XML file, with a header containing participant information, and a body containing utterance text with additional markup (e.g. POS tags). A custom script was used to parse the header. A single ‘target’ child was identified as the listener for this file (some files contained multiple children; a single one was selected to avoid double-counting utterances from the same speakers); the target was selected as the youngest participant whose role was ‘Target_Child’ if there was one, else as the youngest participant whose role was ‘Child’, else as a randomly selected ‘Child’ if there was more than one and age could not be determined. Utterances were then extracted from the file and parsed to determine the speaker (there was no need to determine utterance boundaries since they are marked in CHILDES). Utterances spoken by the target were discarded to isolate the input to the target (only the orthographic form was copied; information such as POS tags was discarded).
Prior to this discard process, utterance and word counts were tallied for each speaker in a ‘social summary’ file. (That is, utterances by the target listener are included in the social summary of the corpus, but they are excluded from the target listener's input.) The speakers were classified by their relationship to the target child, hereafter referred to as ‘role’. Summary statistics are reported below.
A social summary: amount of input by speaker role
CHILDES files contain speaker role information, which made it possible to collect statistics on which talkers said what, and how often. The talker roles listed in CHILDES exhibit a Zipfian distribution in which a few speaker roles occur many times (e.g. Mother, Target_Child) and many roles occur just a few times (e.g. Environment, Toy, Camera_Operator). To simplify presentation, the roles were mapped to a reduced set according to the speaker's relation to the target listener:
• Target – Target_Child, Child
• Investigator – Investigator
• Parent – Mother, Father
• Sibling – Brother, Sister, Sibling
• Family – Grandmother, Grandfather, Aunt, Uncle
• Child – Cousin, Playmate
• Adult – Adult, Camera_Operator, Family_Friend, Teacher, Visitor, Nurse
• Other – any other role not listed here (e.g. Toy, Unidentified, Participant, Group)
Table 1 reports the ten most frequent combinations of speakers present in a document. For example, if only the target child and his/her parent were listed in the document header, then the combination of speakers would be ‘Target, Parent’. This case, as well as ‘Target, Parent, Investigator’, is of particular interest, since in these cases it can be reliably inferred that most or all of the parent's speech was directed to the target child. Beside the question of what combination of speakers was present, it is equally of interest how much input a given role contributes (independent of what other speakers are present); raw and percentage counts are reported in Table 2.

note: Role code and roles columns indicate speaker roles; document count column indicates how many documents had that exact combination of roles; the cumulative percentage of all documents is given in the remaining column. For example, the 64·6% in the cumulative percentage cell of the second row indicates that documents containing just a child and their parent (38·9%) or just a child, their parent, and the investigator (64·5–38 ·9 = 25·6%) jointly make up 64·5% of all documents in the corpus.
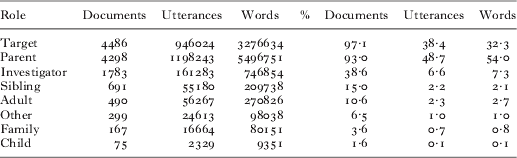
note: Absolute (left) and relative (right) amount of input by speaker role. The # and % columns indicate the role code. Documents columns give the number or percentage of documents in which the role appears. Utterances and words give the number and percentage of utterances and words contributed by each speaker role.
As shown by the top two lines in Table 1, a substantial portion of ‘the input’ analyzed here was directed specifically to the target child. About 65 percent of the interactions documented included only a parent, the child, and the investigator. Since the investigator was there to record the child's natural environment rather than interact with the child's family, it can be inferred that most of the utterances spoken by the parent and investigator were directed toward the child, rather than toward each other. As at least some of the utterances must have been child-directed, even when additional speakers were present, 65 percent represents a very conservative lower bound as to what percentage of ‘the input’ is child-directed.
The reader may wonder why I did not undertake to calculate more exactly the percentage of speech that is child-directed in the corpus as a whole (or restrict my attention only to child-directed utterances). For example, one could imagine selecting a representative sample of corpus files, and coding each utterance binarily as child-directed or not, and reporting the percentage. As it turns out, this is infeasible, owing to issues of selecting a representative sample. The proportion of speech that is child-directed varies enormously across children, and it varies from document to document within-child, and it varies even within a single document; moreover, the documents themselves vary enormously in size. There is no principled criterion by which one could select an a priori representative subsample, and likewise no statistically principled a posteriori means by which one could verify post hoc that the sample was representative. That is the why this ‘social summary’ was conducted.
Preprocessing II: phonological look-up
After preprocessing, a phonological representation of each input file was obtained by dictionary look-up. Each word was replaced by the phonological form listed in the CMU pronouncing dictionary (version 0·7a; https://cmusphinx.svn.sourceforge.net/svnroot/cmusphinx/trunk/cmudict/cmudict.0.7a). The CMU pronouncing dictionary represents standard American phonological forms, e.g. butter is represented as <B AH1 T ER0 > (/`bʌtɝ). Unlisted forms were saved in an error file. Forms that lacked an entry were omitted; the five most frequent unlisted forms for each corpus are given in Table 3.
Table 3. The most frequently occurring forms in CHILDES and the Buckeye corpus not listed in the original dictionary file

While disfluencies and untranscribable elements constitute the bulk of unlisted tokens, many genuine word-forms were also omitted. Examples include peekaboo (frequency=1172), somethin (f=1002), gon (774), Big_Bird (514), d'you (331), num (257), whoopsie (176), Tyrese (146), boing (109), and so on. To guard against the possibility that these items unduly influenced the results, a second pass was performed. The author supplied a phonological transcription for items with a frequency greater than thirty if they constituted a content word (somethin, d'you, Tyrese) rather than an interjection or sound routine (peekaboo, num, whoopsie). The look-up process was repeated with the expanded dictionary, ensuring that only segments from nonwords and low-frequency items were uncounted.
It was not feasible to supply phonological transcriptions for items whose frequency was thirty or less, and which were unlisted in the pronouncing dictionary, owing to the excessively large number of such items (19,000). The reader may get some sense of the untranscribed items from inspecting a list of items randomly selected from the set whose frequency was thirty (x, tent, ann, something's, wendy, landed, big_bird, muffins, return, indians) and items randomly drawn from the entire set (blank 15, ps 1, swinging 24, moat's 1, mona 1, timmy's 16, rainy 13, charmer 4, demolition 1, alternative 1; number after word represents frequency). In the absence of phonological transcriptions, it is not possible to completely rule out the hypothesis that the non-inclusion of these low-frequency items may have meaningfully altered the results. However, this possibility seem unlikely to me. One reason is that in an earlier version of this article, no additional phonological transcriptions were supplied; including these high- and medium-frequency types did not appreciably change the pattern of results. Another reason is that the total frequency of all untranscribed words is a very modest fraction of the words that were included in the child input corpus (84897/10188343 = 0·8%).
Relative frequency counts and data filtering
Each input file was processed by a Python script which counted the number of times each segment occurred. These counts were entered into a tab-separated spreadsheet file, along with additional information such as a unique listener identifier and the listener age at document collection (if identifiable), with each row representing one document. This spreadsheet formed the basis for the experiments reported below, and was read in as a data frame by R.
Prior to conducting the experiments, the samples were filtered. Samples were excluded if they contained less than 100 segments (4–5 utterances), since samples this small do not provide enough data to estimate relative frequencies for stationary, ergodic processes. Child samples were also excluded if the listener's age was greater than 1500 days (4;1·10); this precise value was somewhat arbitrary, and was selected with the goal of concentrating on an age range that unambiguously qualifies as ‘early childhood’, i.e. during which listeners are likely to hear child-directed speech. Finally, child samples were excluded if there were less than ten distinct samples from the same listener; the intention was to ensure that there were enough samples for each listener to reliably estimate listener-specific frequencies (for mixed-effects linear regression, not reported, but see Experiment II results).
EXPERIMENT i: EVEN SEGMENTS ARE BURSTY
Parametric statistics (such as the t-test and ANOVA) are well-established in the social sciences, in part because they make the simple and intuitive assumption that samples are drawn from a stationary, ergodic process. However, if a particular language distribution is not stationary and ergodic, then the use of parametric statistical testing may result in false conclusions. In particular, if the true variance of a process is much higher than the sample variance, there is a greatly inflated risk of a false positive (Type I error). Many types of linguistic distributions follow a power law, and the sample variance for power law distributions is generally far smaller than the true variance (Baayen, Reference Baayen2001). Thus, it is a priori somewhat likely that using parametric statistics to compare linguistic distributions increases the likelihood of a false positive. False positives are a pernicious issue in behavioral research owing to publication bias (Rosenthal, Reference Rosenthal1979), and the bias against publishing null results may be especially strong in child language research. Thus, the goal of Experiment I is to check whether segmental frequency distributions actually are stationary and ergodic.
Experiment I focuses on the distribution of a single segment, /l/, in the child-directed corpora only. The decision to focus on /l/ rather than any other segment was somewhat arbitrary; the only real basis for selection was that it is somewhere in the middle of the frequency spectrum for English segments. Nothing hinges on the particular choice of /l/; the relevant fact is that if the null hypothesis is false for any item, then it is false in general.
The experiment utilized the Monte Carlo method. The logic of this method is to explicitly simulate a process according to some (null) hypothesis, and generate data samples some large number of times (e.g. 1000). The generated data are compared to real data. If the real data differ markedly from the generated data (e.g. more than 95 percent of the generated samples are greater than or less than the real data on some dimension of interest), than the null hypothesis may be rejected. Otherwise, it is concluded that the null hypothesis provides an adequate explanation of the data.
In the case of segmental frequency distributions, the relevant null hypothesis is that the distribution is stationary and ergodic. As noted previously, if a process is truly stationary and ergodic, we know how much variance there should be. If there is significantly more (or less) variance than this, the process must not be stationary and ergodic. Experiment I exploits this reasoning by explicitly generating ‘matched corpora’ with the same number of documents and amount of data in each document, according to the null hypothesis. The variance in the real corpus was then compared to the variance in the generated corpora.
Procedure
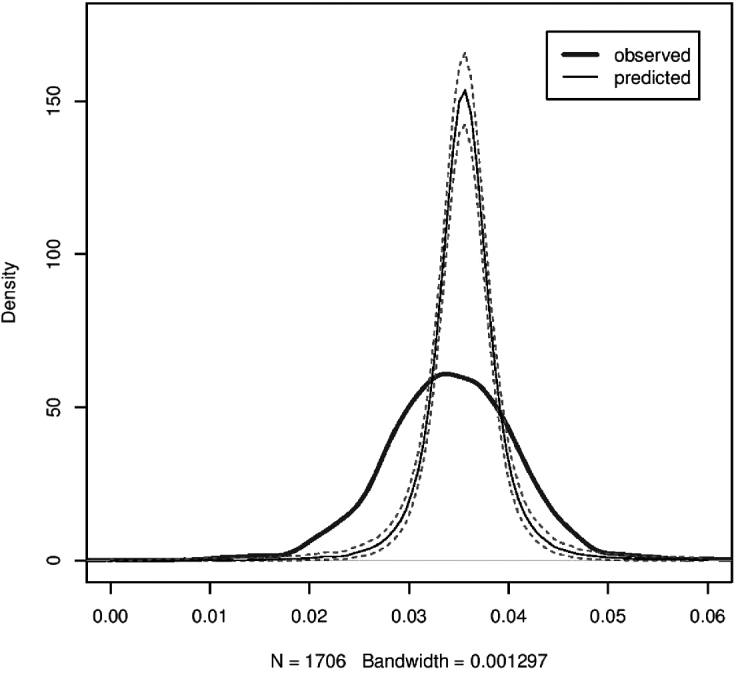
Experiment I was conducted using a custom R script (available from the author's website) running in the 64-bit version of R 2.14.0. As a preliminary, the true probability μ was set to the empirically observed likelihood over the aggregated child corpora (μ/l/ = 0·035). (This guarantees that the mean of the expected distribution will align with the mean of the actual distribution.) A single run R k consisted of the following. For each true document δi in the child corpus of size n[i], a matched document of size n[i] was generated as a sequence of Bernoulli trials: each segment was /l/ with probability μ/l/, and not /l/ otherwise. The generated relative frequency for this document R k,i was defined as the total number of /l/'s generated, divided by n[i]. Thus each run R k consisted of a vector of relative frequencies of [l] (of length m, the number of documents in the child corpus). From each R k, a density distribution ρk was obtained using R's built-in non-parametric kernel density function density(•) with default arguments. One thousand runs (R=R 1..1000) were conducted. The actual density distribution was estimated likewise, except using the actual relative frequencies instead of the generated ones.
The actual distribution and median expected distribution (with confidence intervals) are plotted in Figure 1. The plot was constructed as follows. First, a set of x-values (representing bins of relative likelihood for [l]) was generated by taking 101 evenly spaced points in the range [0,0·06], i.e. the range over which the posterior probability of [l] has support. For a given x-value, the actual y-value was generated by evaluating the actual density distribution at that x-value. In addition, a vector of expected y-values was generated by evaluating each density distribution ρk at the same x-value (1000 values). The median of this vector was used as the predicted y-value; the dashed lines represent the 2·5 and 97·5 percentiles, i.e. the 95 percent confidence interval.
RESULTS
As evident from Figure 1, the actual distribution of relative frequencies of [l] is considerably wider and flatter than the distribution that is expected under the null hypothesis of stationarity and ergodicity. (A p-value is not given because it is not clear how to evaluate p for a whole distribution; in this case it is clear that under any reasonable approach, p would be less than 0·05 since the actual distribution is outside the 95 perent confidence interval for nearly every point on the continuum.) In other words, there is a certain amount of variation around the mean μ/l/ = 0·035 that is predicted by the null hypothesis, but the actual amount of variation is significantly greater.

Fig. 1. Expected versus observed relative frequency density distribution of [l], with 95% confidence intervals.
In terms of the process that generated the child corpora, this can only mean that /l/ is systematically under-represented in some documents relative to its absolute frequency, and likewise over-represented in other documents. Cast in terms of the co-occurrences, the interval between occurrences must be shorter than expected in some documents, and longer in others. Equivalently, /l/ is bursting and lulling, rather than occurring randomly according to its expected frequency. Presumably, this property derives from the fact that some documents contain bursts of words that contain /l/ (e.g. when parents are discussing lemonade, lollipops, etc.).
DISCUSSION
The results showed that there is more variation in the segmental frequency distribution of child input than expected under the unigram assumption. Thus, English segmental frequency distributions are not unigram. This fact has a deeper consequence. Recall that parametric statistical tests such as the t-test and ANOVA assume that samples are drawn from a stationary, ergodic process. Since English segmental frequency distributions are not unigram, it is not in general safe to use parametric statistics on linguistic distributions – doing so will seriously increase the risk of a false positive.
With this fact in hand, it is time to turn to the other aspect of the null hypothesis: Are English segmental frequency distributions unitary? In particular, is the segmental frequency distribution to which children are exposed different from the one adults hear? Since Experiment I showed that it is unsafe to use a t-test or ANOVA to answer this question, Experiment II uses a non-parametric Monte Carlo method to address the question of whether child input is different from adult input.
EXPERIMENT II: SEGMENTAL DISTRIBUTIONS IN CHILD AND ADULT INPUT
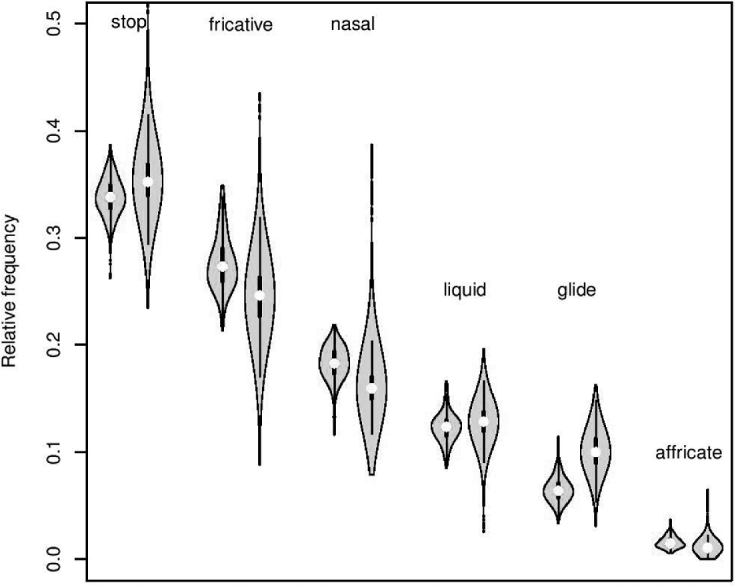
Since Experiment II focuses on consonantal manner classes, relative frequency is calculated with respect to consonants only. Figure 2 uses a violin plot to compare the distribution of relative frequencies of each consonantal manner class in the child and adult input corpora described in Experiment I. A violin plot is akin to both a boxplot and a density plot. For each ‘violin’, the white dot and thick internal lines represent the median and 25th/75th percentiles, and the total height of the violin represents the range of the data after outliers are trimmed – just as with a boxplot. However, the width of the violin varies so as to represent the probability density. Thus, a violin plot conveys whether a distribution is unimodal or not, while this information is not available from a boxplot.

Fig. 2. Violin plot of manner class relative frequencies. Left violins of each pair indicate adult-directed speech; right violins indicate child-directed speech. See text for further details on interpretation.
One fact that is immediately apparent from visually inspecting Figure 2 is that there appear to be some child/adult differences. One difference is that there is inevitably a broader distribution (bigger box) for the child corpus than for the adult corpus. This is a straightforward consequence of the following facts: (i) there are far more child documents than adult documents, and (ii) the child documents are more heterogeneous in length than the adult ones. In other words, this difference plausibly derives from the amount of data available, rather than intrinsic differences between the two language varieties. Beyond this, some of the manners appear to exhibit possibly different distributions; in particular glides appear to be noticeably more frequent in the child corpus than in the adult corpus. These potential differences are the ones of interest. However, just because the medians are visually different on the violin plot, it does not follow that the distributions themselves have different means.
This is because, for all six manners, the relative frequency distributions heavily overlap between the child and adult corpora. That is, nearly all adult documents exhibit a relative frequency vector that is within the normal range for the child corpus, and nearly all child documents exhibit a relative frequency vector that is within the normal range of the adult corpus (one operational definition of ‘normal range’ could be the interval defined by the 2·5 percent and 97·5 percent breakpoints on the cumulative distribution function). Given these facts, it is natural to wonder whether the visual differences from Figure 2 translate into significant statistical differences.
In Experiment II, this question is addressed by repeatedly taking small subsamples from the child and adult corpora and, for each manner, determining how often the mean relative frequency of the manner is greater (smaller) in the child subsample than in the adult subsample. There is no statistical principle that dictates the exact amount of data that should be included in a subsample. What was done here was to set the subsample to include k documents from each corpus, with k varying from 1 to 10. For a given run, here is what occurred. First, k documents were selected randomly (without replacement) from the child corpus, and another k were selected from the adult corpus. Next, the relative frequency of each manner (stop, fricative, affricate, nasal, liquid, and glide) was calculated for each document. For each manner and register, the mean relative frequency was calculated by averaging across all k documents in the subsample. Then, the means were compared. For each manner, a 1 was entered into a vector if the child mean was greater than the adult mean, and 0 was entered otherwise. For each k, 10,000 runs were conducted.
Significance was assessed as follows. For each manner ϕ, the value p ϕ was defined as total number of 1s for manner ϕ, divided by the total number of trials (10,000). This value p ϕ represents the p-value for the one-tailed hypothesis that manner ϕ is more frequent in the child corpus than in the adult corpus. For example, if it was found that the mean relative frequency of glides was greater in the child subsamples than the adult subsamples on ten runs (out of 10,000), then p ϕwould be 0·001. This would constitute strong evidence against the hypothesis that glides are more frequent in child input than in adult input (since in the subsamples, they were actually more frequent in adult input in 99·9 percent of all trials). Thus, extremely low values of p ϕ (close to zero) imply that manner ϕ is more frequent in adult input than in child input, while extremely high values of p ϕ (close to one) imply the opposite. Since there is no prior expectation as to which direction a difference should run, a 2-tailed test is appropriate, meaning the normal significance threshold should be divided by two. Moreover, because six manners are being tested, it is necessary to do a Bonferroni correction, further dividing the significance threshold by six. For the significance threshold α = 0·05 that is standard in social science, we obtain the following:
if p ϕ <α/(2*6) ϕ more frequent in adult input than in child input
p ϕ >1–α/(2*6) ϕ more frequent in child input than adult input
otherwise the two varieties do not differ in relative frequency of ϕ
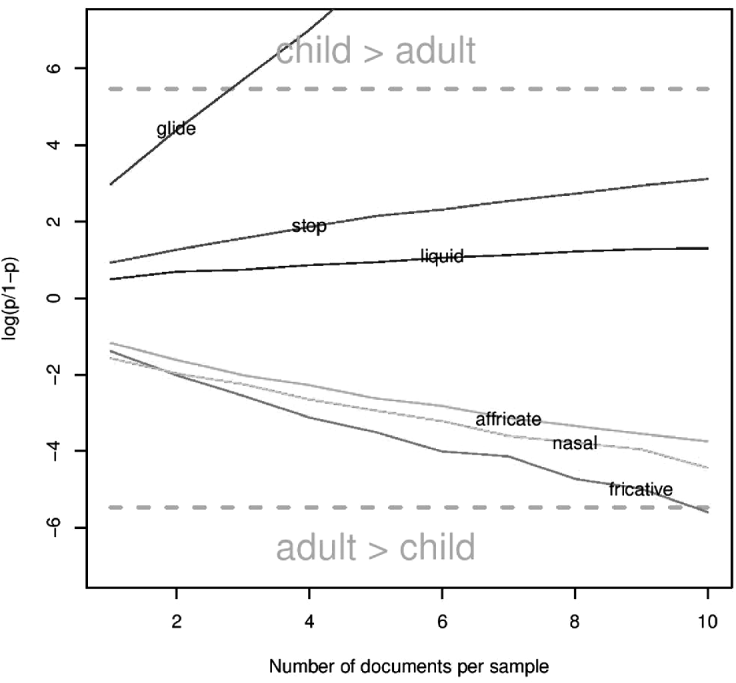
The results are plotted in Figure 3. The x-axis shows k, the number of documents per subsample. The y-axis represents log odds of the p ϕ-value (a log odds transform was done in order to represent the full dynamic range of p ϕ. The dashed lines represent the (log-odds transformed) significance thresholds above.

Fig. 3. Log odds-transformed p-values for each manner class as a function of number of documents in subsamples.
As shown in Figure 3, none of the manners is significant at k = 1. This finding means that if one document were randomly selected from the child input corpus, and another were randomly selected from the adult corpus, there is a non-negligible probability that the child document would have more glides than the adult document, and a non-negligible probability that it would have less (similarly for each of the other manners). However, if the subsample is increased to k = 4 documents, it is now virtually certain that there will be a greater mean relative frequency of glides in the child input.
None of the other manners reaches significance as k is varied, although a clear linear trend is apparent in all cases. One point this suggests is that, while the current data do not actually demonstrate a significant difference for any manner besides glides, there may indeed be small differences in the relative frequency of most manners of articulation between child and adult input. This possibility must be regarded cautiously, for two reasons. The first reason is that the six manners are not independent, so if glides are disproportionately more frequent in adult input, it can only be the case that some combination of other manners must be less frequent. The second reason is that the significance test was not sampling from the entire population, but only resampling from the available sample. This means that the same files were resampled over and over again (particularly from the adult input, where ten files is a substantial fraction of the total corpus). The result is that chance differences will be inflated by the resampling procedure. For example, in the limiting case where the subsample consists of the entire corpus, the ‘significance test’ would necessarily indicate that all manners are significantly different, since the mean relative frequency of each manner will differ across corpora by some small numerical amount even by chance. To generalize beyond the corpora at hand, it is necessary to take subsamples that are sufficiently small; it may not be valid to project much beyond k = 10.
In short, the present results are somewhat inconclusive; glides appear to be genuinely more frequent in child input than in adult input, but at the sensitivity of the present method, no other manner differences emerged as significant. Even if a more sensitive manner could detect child/adult differences, the present results show something very important about the data: if there are any differences between child and adult input in manner relative, they are small or undetectable compared to the level of ‘natural’, background variation present within a variety. The ‘General discussion’ takes up the interesting question of whether such small differences could matter for language development. The next section takes up the question of why glides seem to be more frequent in child input than in adult input.
WHY ARE GLIDES MORE FREQUENT IN CHILD INPUT THAN IN ADULT INPUT?
There is a trivial sense in which the answer to this question can only be that when adults are speaking to children, they use more words that contain glides. This follows from the fact that when adults speak, their speech is almost exhaustively composed of words (rather than, e.g., babbled nonsense syllables). However, there could be two different ways in which adults use more words that contain glides. One way is that there is a small number of glide-containing word types that happen to be far more frequent in child input than in adult input. The other way is if there is a large number of glide-containing word types that are each slightly more frequent in child input than in adult input. I will refer to these as the lexical and phonological explanations, respectively, since the first attributes the glide asymmetry to the frequency of specific lexical items like you, while the second attributes the glide asymmetry to a global preference for words containing glides.
Fortunately, it is possible to collect data bearing on this distinction. Observe that the total frequency of manner ϕ may be expressed as the sum of frequencies contributed by each of the words that contain ϕ. Specifically, define a word ω's contribution to a manner class ϕ's absolute frequency Fr(ϕ | ω) as the number of ϕ's in the word ϕ(ω), multiplied by the number of times the word occurs Fr(ω): Fr(ϕ | ω) = Fr(ω)ϕ(ω). Analogously, ω's contribution to a manner class ϕ's relative frequency may be calculated simply by dividing by the total number of segments: Pr(ϕ | ω) = Fr(ϕ | ω)/F, where F =∑ω ∑ϕ Fr(ϕ | ω).
Crucially, the above definitions can be made variety-specific by calculating frequencies with respect to particular registers, notated here with a subscript (child or adult). By taking the difference, we may quantify the extent to which any particular word contributes to asymmetries in the relative frequency of a particular manner class. Formally, define Δ(ϕ | ω) = Prchild(ϕ | ω) – Pradult(ϕ | ω). The relative frequency asymmetry of manner ϕ between child and adult input Δ(ϕ) must be the sum of Δ(ϕ | ω) across all words. Under the lexical hypothesis, most of this sum will come from a small number of words with a large frequency asymmetry (e.g. you), while under the phonological hypothesis, most of the sum will come from a large number of words with a small frequency asymmetry. Table 4 shows the five words that contribute most to the observed asymmetry, as well as the five words that anti-contribute the most to the observed asymmetry, for two manners, glides and nasal. The total asymmetry is also shown. (Nasals are included because, after glides, they exhibited the strongest numerical difference between child and adult input. As with glides, a few high-frequency words comprise most of the observed numerical difference; so glides do not appear to be unique in this property.)

note: Top five words contributing to the asymmetry between CDS and ADS in the relative frequency of glides (columns 2–3) and nasals (columns 4–5) are shown in the top five data rows. The five words that anti-contribute the most to the total asymmetry are shown in the bottom five data rows. The global manner asymmetry is shown in the bottom row. Positive numbers indicate the manner is more frequent in CDS than in ADS; negative numbers indicate the opposite.
As is evident from inspecting the table, the cumulative distribution of Δ(ϕ | ω) is dominated by a small number of frequent words that exhibit a large frequency asymmetry between child and adult input. In particular, the contribution of the top five glide-contributors to the glide asymmetry is 2·99 percent (1·63 + 0·67 + 0·31 + 0·21 + 0·17), while the total glide asymmetry is 2·96 percent. What this means is that if the words you, what, your, what's, and want were removed from both the child corpus and the adult corpus, the resulting relative frequencies of glides between the child and adult samples would be essentially identical. The same property is exhibited by the nasal manner; the only difference here is that the asymmetry runs in the opposite direction, i.e. nasals are numerically more frequent in the adult corpus than in the child corpus.
In summary, these findings suggest that if there are any significant differences between child and adult in the relative frequency of manner classes – and this study has only found evidence for a glide difference – then they appear to be driven by asymmetries in the relative frequencies of a small number of lexical items. In particular, the glide asymmetry seems to mainly be driven by the fact that you/your and what/what's are more frequent in child input than adult input.
Readers who would like to compare the present results with those of Lee and Davis (Reference Lee and Davis2010) might have noted that the present study studied child input, while that study focused specifically on infant-directed speech. Thus it is possible that the somewhat different findings were caused by the age difference, rather than in the nature of the samples. To address this possibility, a series of mixed-effects linear regressions was carried out. The results are omitted for reasons of space, but may be summarized as follows: (i) there was almost no support for the hypothesis that the segmental frequency distribution changed with a listener's age, nor was there any clear evidence that it varied with the listener; (ii) however, the results of the regression must be regarded as tentative, owing to technical issues arising from sampling sparsity.
GENERAL DISCUSSION
Summary of key findings
The goal of this article was to investigate the amount and causes of frequency variation for manner classes in the input to children and the input to adults. The general findings were:
1. English segmental frequencies lack the unigram property – the between-document variation significantly exceeds what is expected if segments were generated by a stationary, ergodic process.
2. Therefore, it is in general unsafe to use parametric statistics such as the t-test or ANOVA to compare segmental frequency distributions from different language varieties.
3. English segmental frequencies are almost unitary – with the exception of a modest difference in glide frequency, the child and adult input can be modeled as being generated by a single (non-stationary, non-ergodic) source.
4. The aggregate numerical frequency differences in glides between child and adult input appears to have been caused by individual lexical items that are more frequent in child input and happen to contain glides in English (you/your, what/what's, want).
The theme of this article, then, is that between-document variation is large, and other kinds of variation in segmental frequency variation are small or non-existent in comparison. In concert with the findings of Lee and Davis (Reference Lee and Davis2010), whose analysis showed that segmental frequency variation was conditioned by topic-associated words (e.g. p. 773), these findings suggest that topic is an important (albeit indirect) source of variation in segmental frequency: the choice of topic affects which words a speaker chooses, and the words a speaker chooses drives local segmental frequencies.
Implications for segmental acquisition
An immediate, theoretically appealing consequence of these findings is that frequency variation of the type studied here is unlikely to matter for language development. For several logically possible sorts of variation (listener-specific variation, age-graded variation), the mean numerical differences were simply swamped out by the ‘background’ variation in segmental frequencies experienced by every listener – infant, child, and adult. It appears to take frequency asymmetries much larger than this to cause true differences in developmental trajectory. For example, Anderson et al. (Reference Anderson, Morgan and White2003) found that language-specific perception of dorsal stops was acquired one month later than language-specific perception of coronal stops in English-learning infants; the presumptive cause of this rather small developmental asymmetry was a rather large (1:2) asymmetry in token frequency. Similarly, to get a frequency effect, artificial grammar learning studies of phonotactics (Goldrick & Larson, Reference Goldrick, Larson, Fougeron, Kuhnert, D'Imperio and Vallee2010) and morphosyntax (Hudson-Kam & Newport, Reference Hudson Kam and Newport2009) have required much larger asymmetries than the aggregate differences observed here. Thus, while the global frequency of a sound sequence does affect the rate at which it is acquired, we may safely neglect many possible sources of variation across listeners. For example, the next section discusses in more detail this article's claim that the local fluctuations that children experience in segmental frequencies appear to be more or less the same as the ones that adults experience.
How many varieties of a language are there?
One of the primary research questions of this study was whether there were differences in the frequency with which different segmental manners occurred in the input to children versus adults in English. The results of Experiment II were generally in accord with the null hypothesis that child- and adult-directed speech do not differ on this dimension. More precisely, the frequency of glides is slightly higher in the aggregate input to children, owing to high-frequency glide-containing items like you/your and what's/what. Crucially, however, the magnitude of these between-variety differences is quite modest compared to the background level of between-document variability.
There is little reason to expect this kind of asymmetry to generalize across languages: it seems likely that these meanings are indeed more likely to occur in the input to children than to adults in other languages, but it seems rather arbitrary that these lexical forms contain glides in English. For instance, their citation translation equivalents in Russian are /tƗ/ ‘you.Informal.Nom’, /tvo-j/ ‘you.Informal-Adj.Nom.masc’, /çto-/ ‘what-Nom’, /xot-itʲ/ ‘want-Inf’; the only glide in these items comes from the inflectional marker in /tvoj/. In Korean, the translation equivalents are /daŋɕin/ ‘you’, /daŋɕine/ ‘your’, /mwʌ/ ‘what’, and /tɕusejo/ ‘want’; despite containing more segmental material than the English forms, only two of these items contain a glide. Thus, the mild preponderance of glides in the input to English-learning children is likely a statistical accident, rather than reflecting tailoring of caregivers. Of course, in the absence of detailed cross-linguistic work, this conclusion must remain somewhat speculative.
These conclusions contrast with the findings of Lee and Davis (Reference Lee and Davis2010), the only other study to specifically compare segmental frequencies in child- versus adult-directed speech. Those researchers found significant differences for every manner investigated (as well as for other segmental frequencies investigated, such as stop places of articulation). It is natural to ask why and how these two different studies could come to such different conclusions. The answer likely lies in the nature of the samples.
One factor that is not likely to explain the disparity in study conclusions is the raw amount of data. The present study analyzed 492 interactions with child listeners and 150 with adult listeners, with the child samples drawn from a wide variety of social situations, occurring primarily in a child's home. In contrast, Lee and Davis' data consisted of 1000-syllable subsamples drawn from ten mother–child and ten mother–experimenter interactions in a laboratory play session, drawn immediately after the introduction of a small set of toys. The median amount of data per document in the present study is about the same as the amount of data per interaction in Lee and Davis' study; thus the dataset used here is about thirty times the size of the one in Lee and Davis. In general, statistical power does not decrease when there is more data available. Thus, the contrast between a nearly-null result here and the multiple positive results in Lee and Davis' work did not arise because of insufficient data.
Rather, it must have arisen from some other kind of intrinsic difference. More specifically, I would suggest that Lee and Davis' results make a compelling case that new topics are handled differently in speech to infants than speech to adults. As Lee and Davis note (Reference Lee and Davis2010: 780), when mothers are playing with their child and see a new toy, the topic shifts to that toy: the mother repeats its name several times, as well as other words that are associated with it (e.g. actions the toy might perform). In contrast, when a new toy is introduced to a mother who is having a conversation with an adult, she is less likely to name the toy repeatedly and invoke other words associated with it; presumably she simply continues the conversation she is already having. For example, two of the four English toys Lee and Davis named were a pig and a baby; and they found that labial stops were more frequent in speech to infants than to adults. They specifically noted a similar effect for velar-stop-containing toys (p. 780). Since these differences are conditioned by the specific toys involved, they represent properties of the samples rather than properties of infant input versus adult input as a whole.
Both the present study and Lee and Davis (Reference Lee and Davis2010) can be understood, if it is the case that different segmental frequency distributions are induced by different topics. The Lee and Davis study, with its highly controlled toy manipulation, was able to draw out a number of manner-of-articulation (and other) differences between adult samples and child samples, owing to the focus on here-and-now objects and events in child-directed speech (Snow & Ferguson, Reference Snow and Ferguson1977). In contrast, the dataset in the present study contained a variety of topics, and such a diversity of them that the variation across documents washed out most other effects. Taken together, these results suggest that segmental frequency differences will appear between two ‘varieties’ of a language if and only if the topical and lexical distributions of each variety are both highly constrained, and highly different. Otherwise, the natural, ‘background’ between-sample variation will wash out, with the net effect that each variety reflects the more general distribution of the language.
Methodological prescriptions
Aside from the specific theoretical point that child input is not that different from adult input (in terms of segmental frequencies), this article aims to contribute to the field by raising awareness about the sampling issues that arise in language distributions. To this end, the following comments and methodological prescriptions are offered.
(i) The discourse topic can induce large variations in the local segmental frequency. Presumably this point holds even more strongly for other linguistic domains, such as the occurrence of lexical items and syntactic constructions. When comparing two sets of samples, it is important to control the discourse topic to the same extent in both sets.
(ii) The ‘true’ frequency of most linguistic items of interest cannot be reliably estimated. High-frequency items are over-represented in small and medium-sized corpora; low-frequency items are under-represented in corpora of all sizes (Baayen, Reference Baayen2001). Frequency differences between high-frequency items can generally be trusted as revealing real differences in relative frequency; however, the present study showed that even for medium-frequency items like the segment /l/, the variation in frequency across samples can span orders of magnitude.
(iii) In general, it is unsafe to use parametric statistics to compare the frequency of an item or items across language varieties. If it is truly necessary to compare the frequency of an item across two varieties, the researcher is advised to give the utmost care to selecting samples so that they are otherwise matched. The Monte Carlo method of the present study may be of some use; otherwise the researcher might consider reframing their question, or be prepared to devote considerable time to the study of natural language processing and the statistical study of linguistic distributions.
A special concern arising from the bursty distribution of segments is the increased vulnerability to Type I errors (false positives). Of course, in any specific case there may indeed be genuine variation of the type the researcher is interested in. The point here is that the amount of variation is so high that it could generate a positive result even in the absence of a true effect. In other words, in the face of so much variation, positive effects are potentially unreliable; as noted above, false positives may be especially problematic in child language research, since publication bias is potentially quite high in this field. The present study suggests that the discourse topic can introduce large variations in the local frequency of linguistic items of interest, even extremely frequent items.
A philosophically similar point was raised in Tomasello and Stahl (Reference Tomasello and Stahl2004). That study, which was primarily concerned with infrequent constructions, demonstrated empirically that rare phenomena are systematically under-represented, even in quite large longitudinal samples. Furthermore, it showed that aspects of the sampling method strongly influenced the accuracy with which rare items' relative frequencies could be estimated, quite apart from the total amount of speech sampled. However, in that study the conclusion was that the null hypothesis (that the event of interest did not occur in the input) might be falsely accepted, i.e. a Type II error. The present study argues the complementary point that even for relatively frequent items, there is a substantial risk of mis-estimating relative frequency, owing to the large degree of variability between samples. As a result there is an undue risk of falsely rejecting the null hypothesis, i.e. a Type I error.
The upshot of these studies is that whether a researcher is interested in syntax, phonology, semantics, or any other domain of language acquisition, careful attention must be given to how the samples were collected for any kind of naturally occurring data. The social circumstances surrounding data collection – in particular the topic of discussion and other factors that may influence which words are used, as well as the length and frequency of sampling – all have measurable and in some cases known effects on the observed frequency distribution. It is to be hoped that this study underscores the importance of sample considerations in guarding against Type I and Type II errors at all stages of a research project, including data collection, data analysis, data interpretation, and peer review. The positive side of this, from the perspective of design, is that many logically imaginable differences are simply invisible against the backdrop of massive variation that we experience naturally every day, by talking and hearing about a variety of different topics, events, and things.
CONCLUSION
On the basis of the bedrock principle that the form–meaning relationship is arbitrary, it was argued that the null hypothesis should be that for segmental frequencies in particular, child input is not different from adult input. Input frequencies should be a property of the language (unitary), rather than varying between different speech registers; more specifically, we should be able to model the input as a stationary, ergodic process (unigram). The results showed that the null hypothesis was false, but in an interesting way: the amount of variation between documents (each representing a conversation) was very high in comparison to what is predicted by the stationary, ergodic baseline; the magnitude of the between-document variation was very large in comparison to any other effects of interest, such as child/adult differences. Thus, the stationary, ergodic aspect of the null hypothesis was disconfirmed (Experiment I); but the unitary property was shown to be approximately correct (Experiment II). The interesting exception was glides. Although the effect was rather subtle, the results of Experiment II suggested that glides are more frequent in child-directed speech than in adult-directed speech. Taken together, these results suggest the following picture.
When we speak, the sounds that we produce are a function of the words we choose, and we normally choose words to convey a meaning. Thus, the relative frequency of sounds in speech is driven by the relative frequency of the meanings we express. If a particular word is repeated several times, there will of necessity be an increase in the local (short-term) frequencies of the word's sounds. As the topics of conversation are ever-changing, so are the words we use to discuss them, and the sounds they contain. We are all immersed in an ocean of variation, whose global trends may be measured in the aggregate, but whose action is often washed out by the evanescent ebbs and flows of ordinary conversation.