Hostname: page-component-848d4c4894-xfwgj Total loading time: 0 Render date: 2024-06-25T05:40:56.788Z Has data issue: false hasContentIssue false
  • English
  • Français

The winner takes it all but one

Part of: Special processes Operations research and management science Graph theory

Published online by Cambridge University Press:  26 May 2023

Maria Deijfen ,
Remco van der Hofstad  and
Matteo Sfragara
Maria Deijfen*
Affiliation:
Stockholm University
Remco van der Hofstad*
Affiliation:
Eindhoven University of Technology
Matteo Sfragara*
Affiliation:
Stockholm University
*
*Postal address: Department of Mathematics, Albanovägen 28, 106 91 Stockholm, Sweden.
***Postal address: Department of Mathematics and Computer Science, PO Box 513, 5600 MB Eindhoven, The Netherlands. Email address: [email protected]
*Postal address: Department of Mathematics, Albanovägen 28, 106 91 Stockholm, Sweden.
Get access Rights & Permissions [Opens in a new window]

Abstract

We study competing first passage percolation on graphs generated by the configuration model with infinite-mean degrees. Initially, two uniformly chosen vertices are infected with a type 1 and type 2 infection, respectively, and the infection then spreads via nearest neighbors in the graph. The time it takes for the type 1 (resp. 2) infection to traverse an edge e is given by a random variable 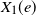$X_1(e)$ (resp. 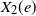$X_2(e)$) and, if the vertex at the other end of the edge is still uninfected, it then becomes type 1 (resp. 2) infected and immune to the other type. Assuming that the degrees follow a power-law distribution with exponent 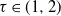$\tau \in (1,2)$, we show that with high probability as the number of vertices tends to infinity, one of the infection types occupies all vertices except for the starting point of the other type. Moreover, both infections have a positive probability of winning regardless of the passage-time distribution. The result is also shown to hold for the erased configuration model, where self-loops are erased and multiple edges are merged, and when the degrees are conditioned to be smaller than 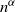$n^\alpha$ for some 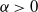$\alpha\gt 0$.

Keywords

Random graphsconfiguration modelfirst passage percolationcompeting growthcoexistence

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Secondary: 05C80: Random graphs 90B15: Network models, stochastic
Type
Original Article
Information
Journal of Applied Probability , Volume 61 , Issue 1 , March 2024 , pp. 137 - 152
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlberg, D., Deijfen, M. and Janson, S. (2019). Competing first passage percolation on random graphs with finite variance degrees. Random Structures Algorithms 55, 545–559.CrossRefGoogle Scholar
Aiello, W., Chung, L. and Lu, L. (2001). A random graph model for power law graphs. Exp. Math. 10, 53–66.CrossRefGoogle Scholar
Albert, R. and Barabási, A.-L. (2002). Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97.CrossRefGoogle Scholar
Antunovic, T., Dekel, Y., Mossel, E. and Peres, Y. (2017). Competing first passage percolation on random regular graphs. Random Structures Algorithms 50, 534–583.CrossRefGoogle Scholar
Auffinger, A., Damron, M. and Hanson, J. (2017). 50 Years of First-Passage Percolation (AMS University Lecture Series 68). American Mathematical Society.CrossRefGoogle Scholar
Baroni, E., van der Hofstad, R. and Komjáthy, J. (2015). Fixed speed competition on the configuration model with infinite variance degrees: unequal speeds. Electron. J. Prob. 20, 1–48.CrossRefGoogle Scholar
Baroni, E., van der Hofstad, R. and Komjáthy, J. (2017). Nonuniversality of weighted random graphs with infinite variance degree. J. Appl. Prob. 54, 146–164.CrossRefGoogle Scholar
Baroni, E., van der Hofstad, R. and Komjáthy, J. (2019). Tight fluctuations of weight-distances in random graphs with infinite-variance degrees. J. Statist. Phys. 174, 906–934.CrossRefGoogle Scholar
Bhamidi, S. and van der Hofstad, R. (2012). Weak disorder asymptotics in the stochastic mean-field model of distance. Ann. Appl. Prob. 22, 29–69.CrossRefGoogle Scholar
Bhamidi, S., van der Hofstad, R. and Hooghiemstra, G. (2010). First passage percolation on random graphs with finite mean degrees. Ann. Appl. Prob. 20, 1907–1965.CrossRefGoogle Scholar
Bhamidi, S., van der Hofstad, R. and Hooghiemstra, G. (2010). Extreme value theory, Poisson–Dirichlet distributions, and first passage percolation on random networks. Adv. Appl. Prob. 42, 706–738.CrossRefGoogle Scholar
Bhamidi, S., van der Hofstad, R. and Hooghiemstra, G. (2017). Universality for first passage percolation on sparse random graphs. Ann. Prob. 45, 2568–2630.CrossRefGoogle Scholar
Bingham, N., Goldie, C. and Teugels, J. (1989). Regular Variation. Cambridge University Press, Cambridge.Google Scholar
Broido, A. and Clauset, A. (2019). Scale-free networks are rare. Nat. Commun. 10, 1017.CrossRefGoogle ScholarPubMed
Deijfen, M. and Häggström, O. (2008). The pleasures and pains of studying the two type Richardson model. In Analysis and Stochastics of Growth Processes and Interface Models, ed. P. Mörters et al., pp. 39–54. Oxford University Press.CrossRefGoogle Scholar
Deijfen, M. and van der Hofstad, R. (2016). The winner takes it all. Ann. Appl. Prob. 26, 2419–2453.CrossRefGoogle Scholar
Garet, O. and Marchand, R. (2005). Coexistence in two-type first-passage percolation models. Ann. Appl. Prob. 15, 298–330.CrossRefGoogle Scholar
Häggström, O. and Pemantle, R. (1998). First passage percolation and a model for competing spatial growth. J. Appl. Prob. 35, 683–692.CrossRefGoogle Scholar
Häggström, O. and Pemantle, R. (2000). Absence of mutual unbounded growth for almost all parameter values in the two-type Richardson model. Stoch. Process. Appl. 90, 207–222.CrossRefGoogle Scholar
Hammersley, J.M. and Welsh, D.J.A. (1965). First passage percolation, subadditive processes, stochastic networks and generalized renewal theory. In Bernoulli 1713, Bayes 1763, Laplace 1813, ed. J. Neyman and L. M. Le Cam, pp. 61–110. Springer.Google Scholar
Hoffman, C. (2005). Coexistence for Richardson type competing spatial growth models. Ann. Appl. Prob. 15, 739–747.CrossRefGoogle Scholar
Janson, S. (2002). On concentration of probability. In Contemporary Combinatorics (Bolyai Society Mathematical Studies 10), pp. 289–301. Springer, Berlin and Heidelberg.Google Scholar
Molloy, M. and Reed, B. (1995). A critical point for random graphs with a given degree sequence. Random Structures Algorithms 6, 161–179.CrossRefGoogle Scholar
Molloy, M. and Reed, B. (1998). The size of the giant component of a random graph with a given degree sequence. Combinatorics Prob. Comput. 7, 295–305.CrossRefGoogle Scholar
Newman, M. E. J. (2003). The structure and function of complex networks. SIAM Rev. 45, 167–256.CrossRefGoogle Scholar
Van den Esker, H., van der Hofstad, R., Hooghiemstra, G. and Znamenski, D. (2005). Distances in random graphs with infinite mean degrees. Extremes 8, 111–141.CrossRefGoogle Scholar
Van der Hofstad, R. (2023). Random Graphs and Complex Networks, volume 2. Available at https://www.win.tue.nl/~rhofstad/NotesRGCNII.pdf.Google Scholar
Van der Hofstad, R. and Komjáthy, J. (2015). Fixed speed competition on the configuration model with infinite variance degrees: equal speeds. Available at arXiv:1503.09046.Google Scholar
Van der Hofstad, R., Hooghiemstra, G. and Van Mieghem, P. (2005). Distances in random graphs with finite variance degrees. Random Structures Algorithms 27, 76–123.CrossRefGoogle Scholar
Van der Hofstad, R., Hooghiemstra, G. and Znamenski, D. (2005). Random graphs with arbitrary i.i.d. degrees. Available at arXiv:math/0502580.Google Scholar
Van der Hofstad, R., Hooghiemstra, G. and Znamenski, D. (2005). Distances in random graphs with finite mean and infinite variance degrees. Electron. J. Prob. 12, 703–766.Google Scholar
Voitalov, I., van der Hoorn, P., van der Hofstad, R. and Krioukov, D. (2019). Scale-free networks well done, Phys. Rev. Res. 1, 033034.CrossRefGoogle Scholar