Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T05:47:32.011Z Has data issue: false hasContentIssue false
  • English
  • Français

Width of a scale-free tree

Part of: Graph theory Combinatorial probability

Published online by Cambridge University Press:  14 July 2016

Zsolt Katona
Zsolt Katona*
Affiliation:
Eötvös Loránd University
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the random graph model of Barabási and Albert, where we add a new vertex in every step and connect it to some old vertices with probabilities proportional to their degrees. If we connect it to only one of the old vertices then this will be a tree. These graphs have been shown to have a power-law degree distribution, the same as that observed in some large real-world networks. 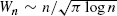We are interested in the width of the tree and we show that it is at the nth step; this also holds for a slight generalization of the model with another constant. We then see how this theoretical result can be applied to directory trees.

Keywords

Random graphscale-free distributionwidth of trees

MSC classification

Primary: 05C80: Random graphs
Secondary: 60C05: Combinatorial probability
Type
Research Papers
Information
Journal of Applied Probability , Volume 42 , Issue 3 , September 2005 , pp. 839 - 850
Copyright
© Applied Probability Trust 2005 

References

Barabási, A.-L. and Albert, R. (1999). Emergence of scaling in random networks. Science 286, 509–512.Google Scholar
Benczúr, A. et al. (2003). Searching a small national domain—Preliminary report. Preprint. Available at http://www.ilab.sztaki.hu/.Google Scholar
Bollobás, B. and Riordan, O. (2004). The diameter of a scale-free random graph. Combinatorica 24, 5–34.CrossRefGoogle Scholar
Bollobás, B., Riordan, O., Spencer, J. and Tusnády, G. (2001). The degree sequence of a scale-free random graph process. Random Structures Algorithms 18, 279–290.Google Scholar
Chauvin, B., Drmota, M. and Jabbour-Hattab, J. (2001). The profile of binary search trees. Ann. Appl. Prob. 11, 1042–1062.Google Scholar
Flajolet, P. and Odlyzko, A. M. (1990). Singularity analysis of generating functions. SIAM J. Discrete Math. 3, 216–240.CrossRefGoogle Scholar
Móri, T. F. (2002). On random trees. Studia Sci. Math. Hung. 39, 143–155.Google Scholar
Pittel, B. (1994). Note on the heights of random recursive trees and random m-ary search trees. Random Structures Algorithms 5, 337–347.Google Scholar
Smythe, R. T. and Mahmoud, H. M. (1994). A survey of recursive trees. Teor. Ĭmovīr. Mat. Stat. 51, 1–29 (in Ukrainian). English translation: Theory Prob. Math. Statist. 51 (1995), 1-27.Google Scholar