Hostname: page-component-f554764f5-sl7kg Total loading time: 0 Render date: 2025-04-12T03:00:59.572Z Has data issue: false hasContentIssue false
  • English
  • Français

Weighted maxima and sums of non-stationary random-length sequences in heavy-tailed models

Part of: Stochastic processes Nonparametric inference

Published online by Cambridge University Press:  02 April 2025

Natalia Markovich Open the ORCID record for Natalia Markovich [Opens in a new window]
Natalia Markovich*
Affiliation:
Russian Academy of Sciences
*
*Postal address: V. A. Trapeznikov Institute of Control Sciences, Russian Academy of Sciences, Profsoyuznaya str. 65, 117997 Moscow, Russia. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Considering a double-indexed array 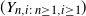$(Y_{n,i:\,n\ge 1,i\ge 1})$ of non-negative regularly varying random variables, we study the random-length weighted sums and maxima from its ‘row’ sequences. These sums and maxima may have the same tail and extremal indices (Markovich and Rodionov 2020). The main constraints of the latter results are that there exists a unique series in a scheme of series with the minimum tail index and the tail of the term number is lighter than the tail of the terms. Here, a bounded random number of series are allowed to have the minimum tail index and the tail of the term number may be heavier than the tail of the terms. We derive the tail and extremal indices of the weighted non-stationary random-length sequences under a broader set of conditions than in Markovich and Rodionov (2020). We provide examples of random sequences for which the assumptions are valid. Perspectives in adopting the results in different application areas are formulated.

Keywords

Random maximarandom sumsregularly varying tailextremal indextail index

MSC classification

Primary: 60G70: Extreme value theory; extremal processes
Secondary: 62G32: Statistics of extreme values; tail inference
Type
Original Article
Information
Journal of Applied Probability , First View , pp. 1 - 20
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ancona-Navarrete, M. A. and Tawn, J. A. (2000). A comparison of methods for estimating the extremal index. Extremes 3, 5–38.Google Scholar
Asmussen, S. (1998). Subexponential asymptotics for stochastic processes: Extremal behavior, stationary distributions and first passage probabilities. Ann. Appl. Prob. 8, 354–374.Google Scholar
Asmussen, S. (2000). Applied Probability and Queues, 2nd edn. Springer, New York.Google Scholar
Asmussen, S. and Foss, S. (2018). Regular variation in a fixed-point problem for single- and multi-class branching processes and queues. Adv. Appl. Prob. 50A, 47–61.CrossRefGoogle Scholar
Beirlant, J., Goegebeur, Y., Teugels, J. and Segers, J. (2004). Statistics of Extremes: Theory and Applications. John Wiley, Chichester.CrossRefGoogle Scholar
Bingham, N. H., Goldie, C. M. and Teugels, J. L. (1987). Regular Variation. Cambridge University Press.Google Scholar
Breiman, L. (1965). On some limit theorems similar to the arc-sin law. Theory Prob. Appl. 10, 323–331.Google Scholar
Dán, G. and Fodor, V. (2009). Delay asymptotics and scalability for peer-to-peer live streaming. IEEE Trans. Parallel Distrib. 20, 1499–1511.Google Scholar
Davis, R. A. and Resnick, S. I. (1996). Limit theory for bilinear processes with heavy-tailed noise. Ann. Appl. Prob. 6, 1191–1210.CrossRefGoogle Scholar
Feitelson, D. (2015). Workload Modeling for Computer Systems Performance Evaluation. Cambridge University Press.CrossRefGoogle Scholar
Gissibl, N. and Klüppelberg, C. (2018). Max-linear models on directed acyclic graphs. Bernoulli 24, 2693–2720.CrossRefGoogle Scholar
Goldaeva, A. A. (2013). Indices of multivariate recurrent stochastic sequences. In Modern Problems of Mathematics and Mechanics, Vol. VIII(3), ed A. N. Shiryaev, Moscow State University, pp. 42–51 (in Russian).Google Scholar
Goldaeva, A. A. and Lebedev, A. V. (2018). On extremal indices greater than one for a scheme of series. Lith. Math. J. 58, 384–398.CrossRefGoogle Scholar
Harchol-Balter, M. and Downey, A. B. (1997). Exploiting process lifetime disributions for dynamic load balancing. ACM Trans. Comput. Syst. 15, 253–285.CrossRefGoogle Scholar
Jelenkovic, P. R. and Olvera-Cravioto, M. (2010). Information ranking and power laws on trees. Adv. Appl. Prob. 42, 1057–1093.Google Scholar
Jelenkovic, P. R. and Olvera-Cravioto, M. (2015). Maximums on trees. Stoch. Process. Appl. 125, 217–232.CrossRefGoogle Scholar
Jessen, A. H. and Mikosch, T. (2006). Regularly varying functions. Publ. Inst. Math. (Beograd) (N.S.) 80, 171–192.Google Scholar
Leadbetter, M. R., Lindgren, G. and Rootzén, H. (1983). Exceedances of levels and kth largest maxima. In Extremes and Related Properties of Random Sequences and Processes, eds M. R. Leadbetter, G. Lindgren and H. Rootzén. Springer, New York, pp. 31–48.Google Scholar
Lebedev, A. V. (2015a). Activity maxima in some models of information networks with random weights and heavy tails. Problems Inf. Transm. 51, 66–74.CrossRefGoogle Scholar
Lebedev, A. V. (2015b). Extremal indices in the series scheme and their applications. Informatics Appl. 9, 39–54 (in Russian).Google Scholar
Litvak, N., Scheinhardt, W. R. W. and Volkovich, Y. (2007). In-degree and PageRank: Why do they follow similar power laws? Internet Math. 4, 175–198.CrossRefGoogle Scholar
Lukashenko, O. V., Morozov, E. V. and Pagano, M. (2019). A Gaussian approximation of the distributed computing process. Informatics Appl. 13, 109–116.Google Scholar
Markovich, N. M. (2013). Quality assessment of the packet transport of peer-to-peer video traffic in high-speed networks. Performance Evaluation 70, 28–44.CrossRefGoogle Scholar
Markovich, N. M. (2023). Extremal properties of evolving networks: Local dependence and heavy tails. Ann. Operat. Res. 339, 1839–1870.CrossRefGoogle Scholar
Markovich, N. M. and Krieger, U. R. (2020). Statistical analysis of the end-to-end delay of packet transfers in a peer-to-peer overlay network. In Proc. 23rd Int. Scientific Conf. Distributed Computer and Communication Networks: Control, Computation, Communications (Lect. Notes Comp. Sci. 12563). Springer, Cham, pp. 282–297.Google Scholar
Markovich, N. M. and Rodionov, I. V. (2020). Maxima and sums of non-stationary random length sequences. Extremes 23, 451–464.CrossRefGoogle Scholar
Markovich, N. M. and Vaičiulis, M. (2023). Extreme value statistics for evolving random networks. Mathematics 11, 2171.CrossRefGoogle Scholar
Olvera-Cravioto, M. (2012). Asymptotics for weighted random sums. Adv. Appl. Prob. 44, 1142–1172.CrossRefGoogle Scholar
Robert, C. Y. and Segers, J. (2008). Tails of random sums of a heavy-tailed number of light-tailed terms. Insurance Math. Econom. 43, 85–92.CrossRefGoogle Scholar
Roberts, G. O., Rosenthal, J., Segers, J. and Sousa, B. (2006). Extremal indices, geometric ergodicity of Markov chains and MCMC. Extremes 9, 213–229.CrossRefGoogle Scholar
Shih, M. F. and Hero, A. O. (2003). Unicast-based inference of network link delay distributions using mixed finite mixture models. IEEE Trans. Sig. Proc. 51, 2219–2228.CrossRefGoogle Scholar
Tillier, C. and Wintenberger, O. (2018). Regular variation of a random length sequence of random variables and application to risk assessment. Extremes 21, 27–56.CrossRefGoogle Scholar
Volkovich, Y. V. and Litvak, N. (2010). Asymptotic analysis for personalized web search. Adv. Appl. Prob. 42, 577–604.Google Scholar