Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-05T21:12:07.772Z Has data issue: false hasContentIssue false
  • English
  • Français

The weak convergence of a class of estimators of the variance function of a two-dimensional Poisson process

Published online by Cambridge University Press:  14 July 2016

A. M. Liebetrau
A. M. Liebetrau*
Affiliation:
The Johns Hopkins University
Get access Rights & Permissions [Opens in a new window]

Abstract

Results of a previous paper (Liebetrau (1977a)) are extended to higher dimensions. An estimator V∗(t1, t2) of the variance function V(t1, t2) of a two-dimensional process is defined, and its first- and second-moment structure is given assuming the process to be Poisson. Members of a class of estimators of the form 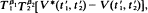where 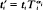and 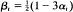for 0 < α i < 1, are shown to converge weakly to a non-stationary Gaussian process. Similar results hold when the t′i are taken to be constants, when V is replaced by a suitable estimator and when the dimensionality of the underlying Poisson process is greater than two.

Keywords

WEAK CONVERGENCEVARIANCE FUNCTIONTWO-DIMENSIONAL POISSON PROCESSMULTIDIMENSIONAL POISSON PROCESSESTIMATOR
Type
Short Communications
Information
Journal of Applied Probability , Volume 15 , Issue 2 , June 1978 , pp. 433 - 439
Copyright
Copyright © Applied Probability Trust 1978 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bickel, P. J. and Wichura, M. J. (1971) Convergence criteria for multiparameter stochastic processes and some applications. Ann. Math. Statist. 42, 1656–1670.CrossRefGoogle Scholar
Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
Fisher, L. (1972) A survey of the mathematical theory of multidimensional point processes. In Stochastic Point Processes: Statistical Analysis, Theory and Applications, ed. Lewis, P. A. W. Wiley, New York, 468–513.Google Scholar
Fraser, D. A. S. (1957) Nonparametric Methods in Statistics. Wiley, New York.Google Scholar
Karlin, S. (1969) A First Course in Stochastic Processes. Academic Press, New York and London.Google Scholar
Liebetrau, A. (1976) Some tests of randomness based upon second-order properties of the Poisson process. Technical Report No. 249, Department of Mathematical Sciences, The Johns Hopkins University. Submitted to J. R. Statist. Soc. B. Google Scholar
Liebetrau, A. (1977a) On the weak convergence of a class of estimators of the variance-time curve of a weakly stationary point process. J. Appl. Prob. 14, 114–126.Google Scholar
Liebetrau, A. (1977b) The weak convergence of a class of estimators of the variance function of a two-dimensional Poisson process. Technical Report No. 258, Department of Mathematical Sciences, The Johns Hopkins University.Google Scholar
Liebetrau, A. and Rothman, E. D. (1977) A classification of spatial distributions based upon several cell sizes. Geographical Analysis 9, 14–28.Google Scholar
Neuhaus, G. (1971) On weak convergence of stochastic processes with multidimensional time parameter. Ann. Math. Statist. 42, 1285–1295.Google Scholar