Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T17:06:12.773Z Has data issue: false hasContentIssue false
  • English
  • Français

A unifying approach to branching processes in a varying environment

Part of: Markov processes Limit theorems

Published online by Cambridge University Press:  04 May 2020

Götz Kersting
Götz Kersting*
Affiliation:
Goethe-Universität, Frankfurt am Main
*
*Postal address: Goethe-Universität Frankfurt am Main, Mathematics and Computer sciences, Frankfurt am Main. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

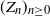Branching processes $(Z_n)_{n \ge 0}$ in a varying environment generalize the Galton–Watson process, in that they allow time dependence of the offspring distribution. Our main results concern general criteria for almost sure extinction, square integrability of the martingale 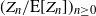$(Z_n/\mathrm E[Z_n])_{n \ge 0}$, properties of the martingale limit W and a Yaglom-type result stating convergence to an exponential limit distribution of the suitably normalized population size 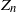$Z_n$, conditioned on the event 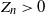$Z_n \gt 0$. The theorems generalize/unify diverse results from the literature and lead to a classification of the processes.

Keywords

Branching processvarying environmentGalton–Watson processexponential distribution

MSC classification

Primary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Secondary: 60F05: Central limit and other weak theorems
Type
Research Papers
Information
Journal of Applied Probability , Volume 57 , Issue 1 , March 2020 , pp. 196 - 220
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Work partially supported by the DFG Priority Programme SPP 1590 ‘Probabilistic Structures in Evolution’.

References

Agresti, A. (1975). On the extinction times of random and varying environment branching processes. J. Appl. Prob. 12, 39–46.CrossRefGoogle Scholar
Bansaye, V. and Simatos, F. (2015). On the scaling limits of Galton Watson processes in varying environment. Electron. J. Prob. 20, 75.CrossRefGoogle Scholar
Bhattacharya, N. and Perlman, M. (2017). Time-inhomogeneous branching processes conditioned on non-extinction. Preprint. arXiv:1703.00337 [math.PR].Google Scholar
Braunsteins, P. and Hautphenne, S. (2019). Extinction in lower Hessenberg branching processes with countably many types. Ann. Appl. Prob. 29, 2782–2818.CrossRefGoogle Scholar
Church, J. D. (1971). On infinite composition products of probability generating functions. Z. Wahrscheinlichkeitsth. 19, 243–256.CrossRefGoogle Scholar
D’Souza, J. C. (1994). The rates of growth of the Galton–Watson process in varying environments. Adv. Appl. Prob. 26, 698–714.CrossRefGoogle Scholar
D’Souza, J. C. and Biggins, J. D. (1992). The supercritical Galton–Watson process in varying environments. Stoch. Process. Appl. 42, 39–47.CrossRefGoogle Scholar
Dolgopyat, D., Hebbar, P., Koralov, L. and Perlman, M. (2018). Multi-type branching processes with time-dependent branching rates. J. Appl. Prob. 55, 701–727.CrossRefGoogle Scholar
Fahady, K. S., Quine, M. P. and Vere Jones, D. (1971). Heavy traffic approximations for the Galton–Watson process. Adv. Appl. Prob. 3, 282–300.CrossRefGoogle Scholar
Fearn, D. H. (1971). Galton–Watson processes with generation dependence. In Proc. 6th Berkeley Symp. Math. Statist. Prob., Vol. 4, University of California Press, Berkeley, CA, pp. 159–172.Google Scholar
Geiger, J. and Kersting, G. (2001). The survival probability of a critical branching process in random environment. Theory Prob. Appl. 45, 517–525.CrossRefGoogle Scholar
Goettge, R. T. (1976). Limit theorems for the supercritical Galton–Watson process in varying environments. Math. Biosci. 28, 171–190.CrossRefGoogle Scholar
González, M., Kersting, G., Minuesa, C. and del Puerto, I. (2019). Branching processes in varying environment with generation dependent immigration. Stoch. Models 35, 148–166.CrossRefGoogle Scholar
Kersting, G. and Vatutin, V. (2017). Discrete Time Branching Processes in Random Environment. John Wiley, New York.CrossRefGoogle Scholar
Jagers, P. (1974). Galton–Watson processes in varying environments. J. Appl. Prob. 11, 174–178.CrossRefGoogle Scholar
Jirina, M. (1976). Extinction of non-homogeneous Galton–Watson processes. J. Appl. Prob. 13, 132–137.CrossRefGoogle Scholar
Lindvall, T. (1974). Almost sure convergence of branching processes in varying and random environments. Ann. Prob. 2, 344–346.CrossRefGoogle Scholar
Lyons, R. (1992). Random walks, capacity and percolation on trees. Ann. Prob. 20, 2043–2088.CrossRefGoogle Scholar
MacPhee, I. M. and Schuh, H. J. (1983). A Galton–Watson branching process in varying environments with essentially constant means and two rates of growth. Austral. J. Statist. 25, 329–338.CrossRefGoogle Scholar
Sagitov, S. and Jagers, J. (2019). Rank-dependent Galton–Watson processes and their pathwise duals. J. Appl. Prob. 50(A), 229–239.Google Scholar
Sevast’yanov, B. A. (1959). Transient phenomena in branching stochastic processes. Theory Prob. Appl. 4, 113–128.CrossRefGoogle Scholar