Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T17:49:33.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Two poisson limit theorems for the coupon collector’s problem with group drawings

Part of: Limit theorems Stochastic processes

Published online by Cambridge University Press:  22 November 2021

Judith Schilling  and
Norbert Henze
Judith Schilling*
Affiliation:
Technische Universität Darmstadt
Norbert Henze*
Affiliation:
Karlsruhe Institute of Technology
*
*Postal address: Fachbereich Mathematik, Technische Universität Darmstadt, Schlossgartenstr. 7, D-64289 Darmstadt, Germany.
**Postal address: Institute of Stochastics, Karlsruhe Institute of Technology (KIT), Englerstr. 2, D-76133 Karlsruhe, Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

In the collector’s problem with group drawings, s out of n different types of coupon are sampled with replacement. In the uniform case, each s-subset of the types has the same probability of being sampled. For this case, we derive a Poisson limit theorem for the number of types that are sampled at most 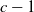$c-1$ times, where 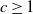$c \ge 1$ is fixed. In a specified approximate nonuniform setting, we prove a Poisson limit theorem for the special case 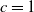$c=1$ . As corollaries, we obtain limit distributions for the waiting time for c complete series of types in the uniform case and a single complete series in the approximate nonuniform case.

Keywords

Coupon collector’s problemgroup drawingsPoisson limit theorem

MSC classification

Primary: 60F05: Central limit and other weak theorems
Secondary: 60G70: Extreme value theory; extremal processes
Type
Original Article
Information
Journal of Applied Probability , Volume 58 , Issue 4 , December 2021 , pp. 966 - 977
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aki, S. and Hirano, K. (2013). Coupon collector’s problems with statistical applications to rankings. Ann. Inst. Statist. Math., 65, 571–587.10.1007/s10463-012-0382-9CrossRefGoogle Scholar
Anceaume, E., Busnel, Y. and Sericola, B. (2015). New results on a generalized coupon collector problem using Markov chains. J. Appl. Prob., 52, 405–418.10.1017/S0021900200012547CrossRefGoogle Scholar
Anceaume, E., Busnel, Y., Schulte-Geers, E. and Sericola, B. (2016). Optimization results for a generalized coupon collector problem. J. Appl. Prob., 53, 622–629.10.1017/jpr.2016.27CrossRefGoogle Scholar
Angus, J. E. (2013). A variation on the coupon collecting problem. Commun. Statist. Simul. Comput., 42, 2197–2202.10.1080/03610918.2012.695845CrossRefGoogle Scholar
Barbour, A. D. and Holst, L. (1989). Some applications of the Stein–Chen method for proving Poisson convergence. Adv. Appl. Prob., 21, 74–90.10.2307/1427198CrossRefGoogle Scholar
Berenbrink, P. and Sauerwald, Th. (2009). The weighted coupon collector’s problem and applications. In Computing and Combinatorics, Proc. 15th Ann. Int. Conf., ed. Ngo, H. Q., Springer, Berlin, pp. 449–458.10.1007/978-3-642-02882-3_45CrossRefGoogle Scholar
Berenbrink, P., Elsässer, R., Friedetzky, T., Nagel, L. and Sauerwald, Th. (2011). Faster coupon collecting via replication with applications in gossiping. In Proc. Int. Symp. Mathematical Foundations of Computer Science 2011, eds. Murlak, F. and Sankowski, P., Springer, Heidelberg, pp. 72–83.10.1007/978-3-642-22993-0_10CrossRefGoogle Scholar
Boneh, A. and Hofri, M. (1997). The coupon-collector problem revisited: A survey of engineering problems and computational methods. Commun. Statist. Stoch. Models, 13, 39–66.10.1080/15326349708807412CrossRefGoogle Scholar
Brown, M. and Ross, S. M. (2016). Optimality results for coupon collection. J. Appl. Prob., 53, 930–937.10.1017/jpr.2016.51CrossRefGoogle Scholar
Brown, M., Peköz, E. and Ross, S. M. (2008). Coupon collecting. Prob. Eng. Inf. Sci., 22, 221–229.10.1017/S0269964808000132CrossRefGoogle Scholar
Dobson, G. and Tezcan, T. (2015). Optimal sampling strategies in the coupon collector’s problem with unknown population size. Ann. Operat. Res., 233, 77–99.10.1007/s10479-014-1563-0CrossRefGoogle Scholar
Doumas, A. and Papanicolaou, V. (2012). The coupon collector’s problem revisited: Asymptotics of the variance. Adv. Appl. Prob., 44, 166–195.10.1239/aap/1331216649CrossRefGoogle Scholar
Doumas, A. and Papanicolaou, V. (2013). Asymptotics of the rising moments for the coupon collector’s problem. Electron. J. Prob., 18, 41.10.1214/EJP.v18-1746CrossRefGoogle Scholar
Erdös, P. and Rényi, A. (1961). On a classical problem of probability theory. Magyar Tud. Akad. Mat. Kutató Int. Közl., 6, 215–220.Google Scholar
Falgas-Ravry, V., Larsson, J. and Markström, K. (2020). Speed and concentration of the covering time for structured coupon collectors. Adv. Appl. Prob., 52, 433–462.10.1017/apr.2020.5CrossRefGoogle Scholar
Ferrante, M. and Saltalamacchia, M. (2014). The coupon collector’s problem. MATerials MATemàtics, 2014, 2.Google Scholar
Fu, J. C. and Lee, W.-C. (2017). On coupon collector’s and Dixie cup problems under fixed and random sample size sampling schemes. Ann. Inst. Statist. Math., 69, 1129–1139.10.1007/s10463-016-0578-5CrossRefGoogle Scholar
Glavaš, L. and Mladenović, P. (2018). New limit results related to the coupon collector’s problem. Studia Sci. Math. Hungar., 55, 115–140.Google Scholar
Graham, R., Knuth, D. and Patashnik, O. (1995). Concrete Mathematics. Addison-Wesley, Boston.Google Scholar
Ilienko, A. (2019). Convergence of point processes associated with coupon collector’s and Dixie cup problems. Electron. Commun. Prob., 24, 51.10.1214/19-ECP263CrossRefGoogle Scholar
Inoue, K. and Aki, S. (2008). Methods for studying generalized birthday and coupon collection problems. Commun. Statist. Simul. Comput., 37, 844–862.10.1080/03610910801943669CrossRefGoogle Scholar
Jocković, J. and Mladenović, P. (2011). Coupon collector’s problem and generalized Pareto distributions. J. Statist. Planning Infer., 141, 2348–2352.10.1016/j.jspi.2011.01.020CrossRefGoogle Scholar
Jocković, J. and Mladenović, P. (2014). Coupon collector’s problem and its extensions in extreme value framework. Stat. Interface, 7, 381–388.10.4310/SII.2014.v7.n3.a8CrossRefGoogle Scholar
Kella, O. and Stadje, W. (2008). A collector’s problem with renewal arrival processes. J. Appl. Prob., 45, 610–620.10.1239/jap/1222441817CrossRefGoogle Scholar
Mahmoud, H. M. (2010). Gaussian phases in generalized coupon collection. Adv. Appl. Prob., 42, 994–1012.10.1239/aap/1293113148CrossRefGoogle Scholar
Mahmoud, H. M. and Smythe, R. T. (2012). On the joint behavior of types of coupons in generalized coupon collection. Adv. Appl. Prob., 44, 429–451.10.1239/aap/1339878719CrossRefGoogle Scholar
May, R. (2008). Coupon collecting with quotas. Electron. J. Combinatorics, 15, 31.10.37236/906CrossRefGoogle Scholar
Mikhailov, V. G. (1977). A Poisson limit theorem in the scheme of group disposal of particles. Theory Prob. Appl., 22, 152–156.10.1137/1122015CrossRefGoogle Scholar
Neal, P. (2008). The generalised coupon collector problem. J. Appl. Prob., 45, 621–629.10.1239/jap/1222441818CrossRefGoogle Scholar
Pósfai, A. and Csórgö, S. (2009). Asymptotic approximations for coupon collectors. Studia Sci. Math. Hungar., 46, 61–96.Google Scholar
Pósfai, A. (2009). Poisson approximation in a Poisson limit theorem inspired by coupon collecting. J. Appl. Prob., 46, 585–592.10.1239/jap/1245676108CrossRefGoogle Scholar
Ross, S. M. and Wu, D. T. (2013). A generalized coupon collecting model as a parsimonious optimal stochastic assignment model. Ann. Operat. Res., 208, 133–146.10.1007/s10479-012-1086-5CrossRefGoogle Scholar
Schilling, J. (2020). Untersuchungen zur Asymptotik und zum Erwartungswert im verallgemeinerten Coupon-Collector-Problem. Doctoral dissertation, Karlsruhe Institute of Technology.Google Scholar
Shank, N. and Yang, H. (2013). Coupon collector problem for non-uniform coupons and random quotas. Electron. J. Combinatorics, 20, 33.10.37236/3348CrossRefGoogle Scholar
Smythe, R. T. (2011). Generalized coupon collection: The superlinear case. J. Appl. Prob., 48, 189–199.10.1017/S0021900200007713CrossRefGoogle Scholar
Stadje, W. (1990). The collector’s problem with group drawings. Adv. Appl. Prob., 22 866–882.10.2307/1427566CrossRefGoogle Scholar
Todhunter, I. (1865). A History of the Mathematical Theory of Probability from the Time of Pascal to that of Laplace. Macmillan, Cambrige.10.5962/bhl.title.31116CrossRefGoogle Scholar
Xu, W. and Tang, A. K. (2011). A generalized coupon collector problem. J. Appl. Prob., 48, 1081–1094.10.1239/jap/1324046020CrossRefGoogle Scholar