No CrossRef data available.
Published online by Cambridge University Press: 10 October 2022
Given a finite strongly connected directed graph
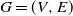 $G=(V, E)$
, we study a Markov chain taking values on the space of probability measures on V. The chain, motivated by biological applications in the context of stochastic population dynamics, is characterized by transitions between states that respect the structure superimposed by E: mass (probability) can only be moved between neighbors in G. We provide conditions for the ergodicity of the chain. In a simple, symmetric case, we fully characterize the invariant probability.
$G=(V, E)$
, we study a Markov chain taking values on the space of probability measures on V. The chain, motivated by biological applications in the context of stochastic population dynamics, is characterized by transitions between states that respect the structure superimposed by E: mass (probability) can only be moved between neighbors in G. We provide conditions for the ergodicity of the chain. In a simple, symmetric case, we fully characterize the invariant probability.