Hostname: page-component-7bb8b95d7b-qxsvm Total loading time: 0 Render date: 2024-09-29T19:51:43.372Z Has data issue: false hasContentIssue false
  • English
  • Français

A time-reversibility relationship between two Markov chains with exponential stationary distributions

Published online by Cambridge University Press:  14 July 2016

M. R. Chernick ,
D. J. Daley  and
R. P. Littlejohn
M. R. Chernick*
Affiliation:
Aerospace Corporation, Los Angeles
D. J. Daley*
Affiliation:
Australian National University
R. P. Littlejohn*
Affiliation:
Invermay Agricultural Research Centre
*
∗Postal address: The Aerospace Corporation, P.O. Box 92957, Los Angeles, CA 90009, USA.
∗∗Postal address: Statistics Department (IAS), The Australian National University, G.P.O. Box 4, Canberra, ACT 2601, Australia.
∗∗∗Postal address: Biometrics Section, Invermay ARC, Private Bag, Mosgiel, New Zealand.
Get access Rights & Permissions [Opens in a new window]

Abstract

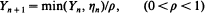The stationary non-negative Markov chains {Yn} and {Xn} specified by the relations for {η n} a sequence of independent identically distributed (i.i.d.) random variables which are independent of {Yn}, and 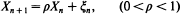for {ξ n} a sequence of i.i.d. random variables which are independent of {Xn}, are mutually time-reversed if and only if their common marginal distribution is exponential, relating the exponential autoregressive process of Gaver and Lewis (1980) to the exponential minification process of Tavares (1980).

Keywords

AUTOREGRESSIVE PROCESSEXPONENTIAL DISTRIBUTIONCHARACTERIZATION
Type
Short Communications
Information
Journal of Applied Probability , Volume 25 , Issue 2 , June 1988 , pp. 418 - 422
Copyright
Copyright © Applied Probability Trust 1988 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Work done in part while visiting the Mathematical Institute, Oxford, with partial support of the Science and Engineering Council.

Work done during the tenure of a Ph.D. scholarship from the Australian National University.

References

Chernick, M. R. (1978) Mixing Conditions and Limit Theorems for Maxima of Some Stationary Sequences. Ph.D. Dissertation, Statistics Department, Stanford University.Google Scholar
Daley, D. J. (1987) A characterization of distributions with exponential and geometric tails (submitted).Google Scholar
Gaver, D. P. and Lewis, P. A. W. (1980) First order autoregressive gamma sequences and point processes. Adv. Appl. Prob. 12, 727–745.Google Scholar
Kelly, F. P. (1979) Reversibility and Stochastic Networks. Wiley, Chichester.Google Scholar
Littlejohn, R. P. (1981) Some Problems Concerning Point Processes. Ph.D. Thesis, Statistics Department (I.A.S.), Australian National University.Google Scholar
Littlejohn, R. P. (1987) The mutual reversibility of two geometric Markovian sequences. (In preparation).Google Scholar
Loynes, R. M. (1965) Extreme values in uniformly mixing stationary stochastic processes. Ann. Math. Statist. 36, 993–999.Google Scholar
Lukacs, E. (1960) Characteristic Functions. Griffin, London.Google Scholar
Mckenzie, E. (1986) Autoregressive moving-average processes with negative-binomial and geometric marginal distribution. Adv. Appl. Prob. 18, 679–705.Google Scholar
Tavares, L. V. (1980) An exponential Markovian stationary process. J. Appl. Prob. 17, 1117–1120. Addendum, J. Appl. Prob. 18, 957.Google Scholar
Weiss, G. (1975) Time-reversibility of linear stochastic processes. J. Appl. Prob. 12, 831–836.Google Scholar