Published online by Cambridge University Press: 01 November 2023
Processes of random tessellations of the Euclidean space 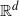 $\mathbb{R}^d$,
$\mathbb{R}^d$, 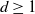 $d\geq 1$, are considered that are generated by subsequent division of their cells. Such processes are characterized by the laws of the life times of the cells until their division and by the laws for the random hyperplanes that divide the cells at the end of their life times. The STIT (STable with respect to ITerations) tessellation processes are a reference model. In the present paper a generalization concerning the life time distributions is introduced, a sufficient condition for the existence of such cell division tessellation processes is provided, and a construction is described. In particular, for the case that the random dividing hyperplanes have a Mondrian distribution—which means that all cells of the tessellations are cuboids—it is shown that the intrinsic volumes, except the Euler characteristic, can be used as the parameter for the exponential life time distribution of the cells.
$d\geq 1$, are considered that are generated by subsequent division of their cells. Such processes are characterized by the laws of the life times of the cells until their division and by the laws for the random hyperplanes that divide the cells at the end of their life times. The STIT (STable with respect to ITerations) tessellation processes are a reference model. In the present paper a generalization concerning the life time distributions is introduced, a sufficient condition for the existence of such cell division tessellation processes is provided, and a construction is described. In particular, for the case that the random dividing hyperplanes have a Mondrian distribution—which means that all cells of the tessellations are cuboids—it is shown that the intrinsic volumes, except the Euler characteristic, can be used as the parameter for the exponential life time distribution of the cells.