Article contents
Stochastic models of damped vibrations
Published online by Cambridge University Press: 14 July 2016
Abstract
In this article we study stochastic perturbations of partial differential equations describing forced-damped vibrations of a string. Two models of such stochastic disturbances are considered; one is triggered by an initial white noise, and the other is in the form of non-Gaussian random forcing. Let uε (t, x) be the displacement at time t of a point x on a string, where the time variable t ≧ 0, and the space variable 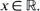 . The small parameter ε controls the intensity of the random fluctuations. The random fields uε (t, x) are shown to satisfy a large deviations principle, and the random deviations of the unperturbed displacement function are analyzed as the noise parameter ε tends to zero.
. The small parameter ε controls the intensity of the random fluctuations. The random fields uε (t, x) are shown to satisfy a large deviations principle, and the random deviations of the unperturbed displacement function are analyzed as the noise parameter ε tends to zero.
MSC classification
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 1996
References
- 7
- Cited by


