1. Introduction
Let ![]() $\mathcal P(\mathcal X)$ denote the space of Borel probability measures over a Polish space
$\mathcal P(\mathcal X)$ denote the space of Borel probability measures over a Polish space ![]() $\mathcal{X}$. Given
$\mathcal{X}$. Given ![]() $\mu,\upsilon\in \mathcal P(\mathcal X)$, denote by
$\mu,\upsilon\in \mathcal P(\mathcal X)$, denote by ![]() $\Gamma(\mu,\upsilon) \;:\!=\; \{\gamma\in\mathcal{P}(\mathcal{X}\times\mathcal{X})\colon\gamma({\mathrm{d}} x,\mathcal{X}) = \mu({\mathrm{d}} x),\,\gamma(\mathcal{X},{\mathrm{d}} y) = \upsilon({\mathrm{d}} y)\}$ the set of couplings (transport plans) with marginals
$\Gamma(\mu,\upsilon) \;:\!=\; \{\gamma\in\mathcal{P}(\mathcal{X}\times\mathcal{X})\colon\gamma({\mathrm{d}} x,\mathcal{X}) = \mu({\mathrm{d}} x),\,\gamma(\mathcal{X},{\mathrm{d}} y) = \upsilon({\mathrm{d}} y)\}$ the set of couplings (transport plans) with marginals ![]() $\mu$ and
$\mu$ and ![]() $\upsilon$. For a fixed, compatible, complete metric d, and given a real number
$\upsilon$. For a fixed, compatible, complete metric d, and given a real number ![]() $p\geq 1$, we define the p-Wasserstein space by
$p\geq 1$, we define the p-Wasserstein space by ![]() $\mathcal W_p(\mathcal{X}) \;:\!=\; \big\{\eta\in\mathcal P(\mathcal{X})\colon\int_{\mathcal{X}}d(x_0,x)^p\,\eta({\mathrm{d}} x) < \infty,\text{ for some }x_0\big\}$. Accordingly, the p-Wasserstein distance between measures
$\mathcal W_p(\mathcal{X}) \;:\!=\; \big\{\eta\in\mathcal P(\mathcal{X})\colon\int_{\mathcal{X}}d(x_0,x)^p\,\eta({\mathrm{d}} x) < \infty,\text{ for some }x_0\big\}$. Accordingly, the p-Wasserstein distance between measures ![]() $\mu,\upsilon\in\mathcal W_p(\mathcal{X})$ is given by
$\mu,\upsilon\in\mathcal W_p(\mathcal{X})$ is given by
When ![]() $p=2$,
$p=2$, ![]() $\mathcal{X}=\mathbb{R}^q$, d is the Euclidean distance, and
$\mathcal{X}=\mathbb{R}^q$, d is the Euclidean distance, and ![]() $\mu$ is absolutely continuous, which is the setting we will soon adopt for the remainder of the paper, Brenier’s theorem [Reference Villani50, Theorem 2.12(ii)] establishes the uniqueness of a minimizer for the right-hand side of (1). Furthermore, this optimizer is supported on the graph of the gradient of a convex function. See [Reference Ambrosio, Gigli and Savaré6, Reference Villani51] for further general background on optimal transport.
$\mu$ is absolutely continuous, which is the setting we will soon adopt for the remainder of the paper, Brenier’s theorem [Reference Villani50, Theorem 2.12(ii)] establishes the uniqueness of a minimizer for the right-hand side of (1). Furthermore, this optimizer is supported on the graph of the gradient of a convex function. See [Reference Ambrosio, Gigli and Savaré6, Reference Villani51] for further general background on optimal transport.
We recall now the definition of the Wasserstein population barycenter.
Definition 1. Given ![]() $\Pi \in \mathcal{P}(\mathcal{P}(\mathcal{X}))$, write
$\Pi \in \mathcal{P}(\mathcal{P}(\mathcal{X}))$, write ![]() $V_p(\bar{m}) \;:\!=\; \int_{\mathcal{P}(\mathcal X)}W_{p}(m,\bar{m})^{p}\,\Pi({\mathrm{d}} m)$. Any measure
$V_p(\bar{m}) \;:\!=\; \int_{\mathcal{P}(\mathcal X)}W_{p}(m,\bar{m})^{p}\,\Pi({\mathrm{d}} m)$. Any measure ![]() $\hat{m}\in\mathcal W_p(\mathcal{X})$ that is a minimizer of the problem
$\hat{m}\in\mathcal W_p(\mathcal{X})$ that is a minimizer of the problem ![]() $\inf_{\bar{m}\in\mathcal{P}(\mathcal X)}V_p(\bar{m})$ is called a p-Wasserstein population barycenter of
$\inf_{\bar{m}\in\mathcal{P}(\mathcal X)}V_p(\bar{m})$ is called a p-Wasserstein population barycenter of ![]() $\Pi$.
$\Pi$.
Wasserstein barycenters were first introduced and analyzed in [Reference Agueh and Carlier1], in the case when the support of ![]() $\Pi\in\mathcal{P}(\mathcal{P}(\mathcal{X}))$ is finite and
$\Pi\in\mathcal{P}(\mathcal{P}(\mathcal{X}))$ is finite and ![]() $\mathcal X=\mathbb{R}^q$. More generally, [Reference Bigot and Klein12, Reference Le Gouic and Loubes38] considered the so-called population barycenter, i.e. the general case in Definition 1 where
$\mathcal X=\mathbb{R}^q$. More generally, [Reference Bigot and Klein12, Reference Le Gouic and Loubes38] considered the so-called population barycenter, i.e. the general case in Definition 1 where ![]() $\Pi$ may have infinite support. These works addressed, among others, the basic questions of the existence and uniqueness of solutions. See also [Reference Kim and Pass35] for the Riemannian case. The concept of the Wasserstein barycenter has been extensively studied from both theoretical and practical perspectives over the last decade: we refer the reader to the overview in [Reference Panaretos and Zemel43] for statistical applications, and to [Reference Cazelles, Tobar and Fontbona17, Reference Cuturi and Doucet26, Reference Cuturi and Peyré27, Reference Peyré and Cuturi44] for computational aspects of optimal transport and applications in machine learning.
$\Pi$ may have infinite support. These works addressed, among others, the basic questions of the existence and uniqueness of solutions. See also [Reference Kim and Pass35] for the Riemannian case. The concept of the Wasserstein barycenter has been extensively studied from both theoretical and practical perspectives over the last decade: we refer the reader to the overview in [Reference Panaretos and Zemel43] for statistical applications, and to [Reference Cazelles, Tobar and Fontbona17, Reference Cuturi and Doucet26, Reference Cuturi and Peyré27, Reference Peyré and Cuturi44] for computational aspects of optimal transport and applications in machine learning.
In this article we develop a stochastic gradient descent (SGD) algorithm for the computation of 2-Wasserstein population barycenters. The method inherits features of the SGD rationale, in particular:
• It exhibits a reduced computational cost compared to methods based on the direct formulation of the barycenter problem using all the available data, as SGD only considers a limited number of samples of
 $\Pi\in\mathcal{P}(\mathcal{P}(\mathcal{X}))$ per iteration.
$\Pi\in\mathcal{P}(\mathcal{P}(\mathcal{X}))$ per iteration.-
• It is online (or continual, as referred to in the machine learning community), meaning that it can incorporate additional datapoints sequentially to update the barycenter estimate whenever new observations becomes available. This is relevant even when
 $\Pi$ is finitely supported.
$\Pi$ is finitely supported. • Conditions ensuring convergence towards the Wasserstein barycenter as well as finite-dimensional convergence rates for the algorithm can be provided. Moreover, the variance of the gradient estimators can be reduced by using mini-batches.
From now on we make the following assumption.
Assumption 1. ![]() $\mathcal X=\mathbb{R}^q$, d is the squared Euclidean metric, and
$\mathcal X=\mathbb{R}^q$, d is the squared Euclidean metric, and ![]() $p=2$.
$p=2$.
We denote by ![]() $\mathcal W_{2,\mathrm{ac}}(\mathcal X)$ the subspace of
$\mathcal W_{2,\mathrm{ac}}(\mathcal X)$ the subspace of ![]() $\mathcal W_{2}(\mathcal X)$ of absolutely continuous measures with finite second moment and, for any
$\mathcal W_{2}(\mathcal X)$ of absolutely continuous measures with finite second moment and, for any ![]() $\mu\in\mathcal W_{2,\mathrm{ac}}(\mathcal X)$ and
$\mu\in\mathcal W_{2,\mathrm{ac}}(\mathcal X)$ and ![]() $\nu\in\mathcal W_{2}(\mathcal X)$ we write
$\nu\in\mathcal W_{2}(\mathcal X)$ we write ![]() $T_\mu^\nu$ for the (
$T_\mu^\nu$ for the (![]() $\mu$-almost sure, unique) gradient of a convex function such that
$\mu$-almost sure, unique) gradient of a convex function such that ![]() $T_\mu^\nu(\mu)=\nu$. Notice that
$T_\mu^\nu(\mu)=\nu$. Notice that ![]() $x\mapsto T_{\mu}^{\nu}(x)$ is a
$x\mapsto T_{\mu}^{\nu}(x)$ is a ![]() $\mu$-almost sure (a.s.) defined map and that we use throughout the notation
$\mu$-almost sure (a.s.) defined map and that we use throughout the notation ![]() $T_\mu^\nu(\rho)$ for the image measure/law of this map under the measure
$T_\mu^\nu(\rho)$ for the image measure/law of this map under the measure ![]() $\rho$.
$\rho$.
Recall that a set ![]() $B\subset\mathcal W_{2,\mathrm{ac}}(\mathcal X)$ is geodesically convex if, for every
$B\subset\mathcal W_{2,\mathrm{ac}}(\mathcal X)$ is geodesically convex if, for every ![]() $\mu,\nu\in B$ and
$\mu,\nu\in B$ and ![]() $t\in[0,1]$ we have
$t\in[0,1]$ we have ![]() $((1-t)I+tT_\mu^\nu)(\mu)\in B$, with I denoting the identity operator. We will also assume the following condition for most of the article.
$((1-t)I+tT_\mu^\nu)(\mu)\in B$, with I denoting the identity operator. We will also assume the following condition for most of the article.
Assumption 2. ![]() $\Pi$ gives full measure to a geodesically convex
$\Pi$ gives full measure to a geodesically convex ![]() $W_2$-compact set
$W_2$-compact set ![]() $K_\Pi\subset\mathcal W_{2,\mathrm{ac}}(\mathcal X)$.
$K_\Pi\subset\mathcal W_{2,\mathrm{ac}}(\mathcal X)$.
In particular, under Assumption 2 we have ![]() $\int_{\mathcal P(\mathcal X)}\int_{\mathcal X}d(x,x_0)^2\,m({\mathrm{d}} x)\,\Pi({\mathrm{d}} m)<\infty$ for all
$\int_{\mathcal P(\mathcal X)}\int_{\mathcal X}d(x,x_0)^2\,m({\mathrm{d}} x)\,\Pi({\mathrm{d}} m)<\infty$ for all ![]() $x_0$. Moreover, for each
$x_0$. Moreover, for each ![]() $\nu\in\mathcal W_2(\mathcal X)$ and
$\nu\in\mathcal W_2(\mathcal X)$ and ![]() $\Pi(dm)$ for almost every (a.e.) m, there is a unique optimal transport map
$\Pi(dm)$ for almost every (a.e.) m, there is a unique optimal transport map ![]() $T_m^\nu$ from m to
$T_m^\nu$ from m to ![]() $\nu$ and, by [Reference Le Gouic and Loubes38, Proposition 6], the 2-Wasserstein population barycenter is unique.
$\nu$ and, by [Reference Le Gouic and Loubes38, Proposition 6], the 2-Wasserstein population barycenter is unique.
Definition 2. Let ![]() $\mu_0 \in K_\Pi$,
$\mu_0 \in K_\Pi$, ![]() $m_k \stackrel{\mathrm{i.i.d.}}{\sim} \Pi$, and
$m_k \stackrel{\mathrm{i.i.d.}}{\sim} \Pi$, and ![]() $\gamma_k > 0$ for
$\gamma_k > 0$ for ![]() $k \geq 0$. We define the stochastic gradient descent (SGD) sequence by
$k \geq 0$. We define the stochastic gradient descent (SGD) sequence by
The reasons why we can truthfully refer to the above sequence as stochastic gradient descent will become apparent in Sections 2 and 3. We stress that the sequence is a.s. well defined, as we can show by induction that ![]() $\mu_k\in \mathcal W_{2,\mathrm{ac}}(\mathcal X)$ a.s. thanks to Assumption 2. We also refer to Section 3 for remarks on the measurability of the random maps
$\mu_k\in \mathcal W_{2,\mathrm{ac}}(\mathcal X)$ a.s. thanks to Assumption 2. We also refer to Section 3 for remarks on the measurability of the random maps ![]() $\{T_{\mu_k}^{m_k}\}_k$ and sequence
$\{T_{\mu_k}^{m_k}\}_k$ and sequence ![]() $\{\mu_k\}_k$.
$\{\mu_k\}_k$.
Throughout the article, we assume the following conditions on the steps ![]() $\gamma_k$ in (2), commonly required for the convergence of SGD methods:
$\gamma_k$ in (2), commonly required for the convergence of SGD methods:
In addition to barycenters, we will need the concept of Karcher means (cf. [Reference Zemel and Panaretos55]), which, in the setting of the optimization problem in ![]() $\mathcal W_{2,\mathrm{ac}}(\mathcal X)$ considered here, can be intuitively understood as an analogue of a critical point of a smooth function in Euclidean space (see the discussion in Section 2).
$\mathcal W_{2,\mathrm{ac}}(\mathcal X)$ considered here, can be intuitively understood as an analogue of a critical point of a smooth function in Euclidean space (see the discussion in Section 2).
Definition 3. Given ![]() $\Pi\in\mathcal{P}(\mathcal{P}(\mathcal{X}))$, we say that
$\Pi\in\mathcal{P}(\mathcal{P}(\mathcal{X}))$, we say that ![]() $\mu\in\mathcal W_{2,\mathrm{ac}}(\mathcal X)$ is a Karcher mean of
$\mu\in\mathcal W_{2,\mathrm{ac}}(\mathcal X)$ is a Karcher mean of ![]() $\Pi$ if
$\Pi$ if ![]() $\mu\big(\big\{x\colon x = \int_{m\in\mathcal P(\mathcal X)}T_\mu^m(x)\,\Pi({\mathrm{d}} m)\big\}\big)=1$.
$\mu\big(\big\{x\colon x = \int_{m\in\mathcal P(\mathcal X)}T_\mu^m(x)\,\Pi({\mathrm{d}} m)\big\}\big)=1$.
It is known that any 2-Wasserstein barycenter is a Karcher mean, though the latter is in general a strictly larger class; see [Reference Álvarez-Esteban, del Barrio, Cuesta-Albertos and Matrán4] or Example 1. However, if there is a unique Karcher mean, then it must coincide with the unique barycenter. We can now state the main result of the article.
Theorem 1. We assume Assumptions 1 and 2, conditions (3) and (4), and that the 2-Wasserstein barycenter ![]() $\hat{\mu}$ of
$\hat{\mu}$ of ![]() $\Pi$ is the unique Karcher mean. Then, the SGD sequence
$\Pi$ is the unique Karcher mean. Then, the SGD sequence ![]() $\{\mu_k\}_k$ in (2) is a.s.
$\{\mu_k\}_k$ in (2) is a.s. ![]() $\mathcal W_2$-convergent to
$\mathcal W_2$-convergent to ![]() $\hat{\mu}\in K_\Pi$.
$\hat{\mu}\in K_\Pi$.
An interesting aspect of Theorem 1 is that it hints at a law of large numbers (LLN) on the 2-Wasserstein space. Indeed, in the conventional LLN, for i.i.d. samples ![]() $X_i$ the summation
$X_i$ the summation ![]() $S_{k}\;:\!=\;({1}/{k})\sum_{i\leq k}X_i$ can be expressed as
$S_{k}\;:\!=\;({1}/{k})\sum_{i\leq k}X_i$ can be expressed as
Therefore, if we rather think of sample ![]() $X_k$ as a measure
$X_k$ as a measure ![]() $m_k$ and of
$m_k$ and of ![]() $S_k$ as
$S_k$ as ![]() $\mu_k$, we immediately see the connection with
$\mu_k$, we immediately see the connection with
obtained from (2) when we take ![]() $\gamma_k={1}/({k+1})$. The convergence in Theorem 1 can thus be interpreted as an analogy to the convergence of
$\gamma_k={1}/({k+1})$. The convergence in Theorem 1 can thus be interpreted as an analogy to the convergence of ![]() $S_k$ to the mean of
$S_k$ to the mean of ![]() $X_1$ (we thank Stefan Schrott for this observation).
$X_1$ (we thank Stefan Schrott for this observation).
In order to state our second main result, Theorem 2, we first introduce a new concept.
Definition 4. Given ![]() $\Pi\in\mathcal{P}(\mathcal{P}(\mathcal{X}))$ we say that a Karcher mean
$\Pi\in\mathcal{P}(\mathcal{P}(\mathcal{X}))$ we say that a Karcher mean ![]() $\mu\in\mathcal W_{2,\mathrm{ac}}(\mathcal X)$ of
$\mu\in\mathcal W_{2,\mathrm{ac}}(\mathcal X)$ of ![]() $\Pi$ is pseudo-associative if there exists
$\Pi$ is pseudo-associative if there exists ![]() $C_{\mu}>0$ such that, for all
$C_{\mu}>0$ such that, for all ![]() $\nu\in\mathcal W_{2,\mathrm{ac}}(\mathcal{X})$,
$\nu\in\mathcal W_{2,\mathrm{ac}}(\mathcal{X})$,
Since the term on the right-hand side of (5) vanishes for any Karcher mean ![]() $\nu$, the existence of a pseudo-associative Karcher mean implies
$\nu$, the existence of a pseudo-associative Karcher mean implies ![]() $\mu=\nu$, hence uniqueness of Karcher means. We will see that, moreover, the existence of a pseudo-associative Karcher mean implies a Polyak–Lojasiewicz inequality for the functional minimized by the barycenter, see (20). This in turn can be utilized to obtain convergence rates for the expected optimality gap in a similar way to the Euclidean case. While the pseudo-associativity condition is a strong requirement, in the following result we are able to weaken Assumption 2 into the following milder assumption.
$\mu=\nu$, hence uniqueness of Karcher means. We will see that, moreover, the existence of a pseudo-associative Karcher mean implies a Polyak–Lojasiewicz inequality for the functional minimized by the barycenter, see (20). This in turn can be utilized to obtain convergence rates for the expected optimality gap in a similar way to the Euclidean case. While the pseudo-associativity condition is a strong requirement, in the following result we are able to weaken Assumption 2 into the following milder assumption.
Assumption 2′. ![]() $\Pi$ gives full measure to a geodesically convex set
$\Pi$ gives full measure to a geodesically convex set ![]() $K_\Pi\subset\mathcal W_{2,\mathrm{ac}}(\mathcal X)$ that is
$K_\Pi\subset\mathcal W_{2,\mathrm{ac}}(\mathcal X)$ that is ![]() $\mathcal W_2$-bounded (i.e.
$\mathcal W_2$-bounded (i.e. ![]() $\sup_{m\in K_\Pi}\int |x|^2\,m({\mathrm{d}} x)<\infty$).
$\sup_{m\in K_\Pi}\int |x|^2\,m({\mathrm{d}} x)<\infty$).
Clearly this condition is equivalent to requiring that the support of ![]() $\Pi$ be
$\Pi$ be ![]() $\mathcal W_2$-bounded and consist of absolutely continuous measures.
$\mathcal W_2$-bounded and consist of absolutely continuous measures.
We now present our second main result.
Theorem 2. We assume Assumptions 1 and 2′, and that the 2-Wasserstein barycenter ![]() $\hat{\mu}$ of
$\hat{\mu}$ of ![]() $\Pi$ is a pseudo-associative Karcher mean. Then,
$\Pi$ is a pseudo-associative Karcher mean. Then, ![]() $\hat{\mu}$ is the unique barycenter of
$\hat{\mu}$ is the unique barycenter of ![]() $\Pi$, and the SGD sequence
$\Pi$, and the SGD sequence ![]() $\{\mu_k\}_k$ in (2) is a.s. weakly convergent to
$\{\mu_k\}_k$ in (2) is a.s. weakly convergent to ![]() $\hat{\mu}\in K_\Pi$ as soon as (3) and (4) hold. Moreover, for every
$\hat{\mu}\in K_\Pi$ as soon as (3) and (4) hold. Moreover, for every ![]() $a>C_{\hat{\mu}}^{-1}$ and
$a>C_{\hat{\mu}}^{-1}$ and ![]() $b\geq a$ there exists an explicit constant
$b\geq a$ there exists an explicit constant ![]() $C_{a,b}>0$ such that, if
$C_{a,b}>0$ such that, if ![]() $\gamma_k={a}/({b+k})$ for all
$\gamma_k={a}/({b+k})$ for all ![]() $k\in\mathbb{N}$, the expected optimality gap satisfies
$k\in\mathbb{N}$, the expected optimality gap satisfies
Let us explain the reason for the terminology ‘pseudo-associative’ we have chosen. This comes from the fact that the inequality in Definition 4 holds true (with equality and ![]() $C_{\mu}=1$) as soon as the associativity property
$C_{\mu}=1$) as soon as the associativity property ![]() $T_{\mu}^{m}(x) = T_{\nu}^m \circ T_{\mu}^{\nu}(x)$ holds
$T_{\mu}^{m}(x) = T_{\nu}^m \circ T_{\mu}^{\nu}(x)$ holds ![]() $\mu({\mathrm{d}} x)$-a.s. for each pair
$\mu({\mathrm{d}} x)$-a.s. for each pair ![]() $\nu,m\in W_{2,\mathrm{ac}}(\mathcal X)$; see Remark 2. The previous identity was assumed to hold for the results proved in [Reference Bigot and Klein12], and is always valid in
$\nu,m\in W_{2,\mathrm{ac}}(\mathcal X)$; see Remark 2. The previous identity was assumed to hold for the results proved in [Reference Bigot and Klein12], and is always valid in ![]() $\mathbb{R}$, since the composition of monotone functions is monotone. Further examples where the associativity property holds are discussed in Section 6. Thus, in all those settings, (5) and Theorem 2 hold as soon as Assumption 2′ is granted, and, further, we have the explicit LLN-like expression
$\mathbb{R}$, since the composition of monotone functions is monotone. Further examples where the associativity property holds are discussed in Section 6. Thus, in all those settings, (5) and Theorem 2 hold as soon as Assumption 2′ is granted, and, further, we have the explicit LLN-like expression ![]() $\mu_{k+1}=\big(({1}/{k})\sum_{i=1}^k T_{\mu_0}^{m_i}\big)(\mu_0)$. As regards the more general pseudo-associativity property, we will see that it holds, for instance, in the Gaussian framework studied in [Reference Chewi, Maunu, Rigollet and Stromme19], and in certain classes of scatter-location families, which we discuss in Section 6.
$\mu_{k+1}=\big(({1}/{k})\sum_{i=1}^k T_{\mu_0}^{m_i}\big)(\mu_0)$. As regards the more general pseudo-associativity property, we will see that it holds, for instance, in the Gaussian framework studied in [Reference Chewi, Maunu, Rigollet and Stromme19], and in certain classes of scatter-location families, which we discuss in Section 6.
The remainder of the paper is organized as follows:
• In Section 2 we recall basic ideas and results on gradient descent algorithms for Wasserstein barycenters.
-
• In Section 3 we prove Theorem 1, providing the technical elements required to that end.
-
• In Section 4 we discuss the notion of pseudo-associative Karcher means and their relation to the so-calledPolyak–Lojasiewicz and variance inequalities, and we prove Theorem 2.
-
• In Section 5 we introduce the mini-batch version of our algorithm, discuss how this improves the variance of gradient-type estimators, and state extensions of our previous results to that setting.
-
• In Section 6 we consider closed-form examples and explain how in these cases the existence of pseudo-associative Karcher means required in Theorem 2 can be guaranteed. We also explore certain properties of probability distributions that are ‘stable’ under the operation of taking their barycenters.
In the remainder of this introduction we provide independent discussions on various aspects of our results (some of them suggested by the referees) and on related literature.
1.1. On the assumptions
Although Assumption 2 might appear strong at first sight, it can be guaranteed in suitable parametric situations (e.g. Gaussian, or the scatter-location setting recalled in Section 6.4) or, more generally, under moment and density constraints on the measures in ![]() $K_\Pi$. For instance, if
$K_\Pi$. For instance, if ![]() $\Pi$ is supported on a finite set of measures with finite Boltzmann entropy, then Assumption 2 is guaranteed. More generally, if the support of
$\Pi$ is supported on a finite set of measures with finite Boltzmann entropy, then Assumption 2 is guaranteed. More generally, if the support of ![]() $\Pi$ is a 2-Wasserstein compact set and the Boltzmann entropy is uniformly bounded on it, then Assumption 2 is fulfilled too: see Lemma 3.
$\Pi$ is a 2-Wasserstein compact set and the Boltzmann entropy is uniformly bounded on it, then Assumption 2 is fulfilled too: see Lemma 3.
The conditions of Assumption 2 and the uniqueness of a Karcher mean in Theorem 1 are natural substitutes for, respectively, the compactness of SGD sequences and the uniqueness of critical points, which hold under ther usual sets of assumptions ensuring the convergence of SGD in Euclidean space to a minimizer, e.g. some growth control and certain strict convexity-type conditions at a minimum. The usual reasoning underlying the convergence analysis of SGD in Euclidean spaces, however, seem not to be applicable in our context, as the functional ![]() $\mathcal W_{2,\mathrm{ac}}(\mathcal X)\ni\mu\mapsto F(\mu)\;:\!=\;\int W_{2}(m,\bar{m})^{2}\,\Pi({\mathrm{d}} m)$ is not convex, in fact not even
$\mathcal W_{2,\mathrm{ac}}(\mathcal X)\ni\mu\mapsto F(\mu)\;:\!=\;\int W_{2}(m,\bar{m})^{2}\,\Pi({\mathrm{d}} m)$ is not convex, in fact not even ![]() $\alpha$-convex for some
$\alpha$-convex for some ![]() $\alpha\in\mathbb R$, when
$\alpha\in\mathbb R$, when ![]() $\mathcal W_{2,\mathrm{ac}}(\mathcal X)$ is endowed with its almost Riemannian structure induced by optimal transport (see [Reference Ambrosio, Gigli and Savaré6, Chapter 7.2]). The function F is also not
$\mathcal W_{2,\mathrm{ac}}(\mathcal X)$ is endowed with its almost Riemannian structure induced by optimal transport (see [Reference Ambrosio, Gigli and Savaré6, Chapter 7.2]). The function F is also not ![]() $\alpha$-convex for some
$\alpha$-convex for some ![]() $\alpha\in\mathbb R$ when we use generalized geodesics (see [Reference Ambrosio, Gigli and Savaré6, Chapter 9.2]). In fact, SGD in finite-dimensional Riemannian manifolds could provide a more suitable framework to draw inspiration from; see, e.g., [Reference Bonnabel13]. Ideas useful in that setting seem not straightforward to leverage since that work either assumes negative curvature (while
$\alpha\in\mathbb R$ when we use generalized geodesics (see [Reference Ambrosio, Gigli and Savaré6, Chapter 9.2]). In fact, SGD in finite-dimensional Riemannian manifolds could provide a more suitable framework to draw inspiration from; see, e.g., [Reference Bonnabel13]. Ideas useful in that setting seem not straightforward to leverage since that work either assumes negative curvature (while ![]() $\mathcal W_{2,\mathrm{ac}}(\mathcal X)$ is positively curved), or that the functional to be minimized be rather smooth and have bounded derivatives of first and second order.
$\mathcal W_{2,\mathrm{ac}}(\mathcal X)$ is positively curved), or that the functional to be minimized be rather smooth and have bounded derivatives of first and second order.
The assumption that ![]() $K_\Pi$ is contained in a subset of
$K_\Pi$ is contained in a subset of ![]() $\mathcal W_{2}(\mathcal X)$ of absolutely continuous probability measures, and hence the existence of optimal transport maps between elements of
$\mathcal W_{2}(\mathcal X)$ of absolutely continuous probability measures, and hence the existence of optimal transport maps between elements of ![]() $K_\Pi$, appears as a more structural requirement, as it is needed to construct the iterations in (2). Indeed, by dealing with an extended notion of Karcher mean, it is in principle also possible to define an analogous iterative scheme in a general setting, including in particular the case of discrete laws, and thus to relax to some extent the absolute continuity requirement. However, this introduces additional technicalities, and we unfortunately were not able to provide conditions ensuring the convergence of the method in reasonably general situations. For completeness of the discussion, we sketch the main ideas of this possible extension in the Appendix.
$K_\Pi$, appears as a more structural requirement, as it is needed to construct the iterations in (2). Indeed, by dealing with an extended notion of Karcher mean, it is in principle also possible to define an analogous iterative scheme in a general setting, including in particular the case of discrete laws, and thus to relax to some extent the absolute continuity requirement. However, this introduces additional technicalities, and we unfortunately were not able to provide conditions ensuring the convergence of the method in reasonably general situations. For completeness of the discussion, we sketch the main ideas of this possible extension in the Appendix.
1.2. Uniqueness of Karcher means
Regarding situations where uniqueness of Karcher means can be granted, we refer to [Reference Panaretos and Zemel43, Reference Zemel and Panaretos55] for sufficient conditions when the support of ![]() $\Pi$ is finite, based on the regularity theory of optimal transport, and to [Reference Bigot and Klein12] for the case of an infinite support, under rather strong assumptions. We remark also that in one dimension, the uniqueness of Karcher means is known to hold without further assumptions. A first counterexample where this uniqueness is not guaranteed is given in [Reference Álvarez-Esteban, del Barrio, Cuesta-Albertos and Matrán4]; see also the simplified Example 1. A general understanding of the uniqueness of Karcher means remains an open and interesting challenge, however. This is not only relevant for the present work, but also for the (non-stochastic) gradient descent method of [Reference Zemel and Panaretos55] and the fixed-point iterations of [Reference Álvarez-Esteban, del Barrio, Cuesta-Albertos and Matrán4]. The notion of pseudo-associativity introduced in Definition 4 provides an alternative viewpoint on this question, complementary to the aforementioned ones, which might deserve being further explored.
$\Pi$ is finite, based on the regularity theory of optimal transport, and to [Reference Bigot and Klein12] for the case of an infinite support, under rather strong assumptions. We remark also that in one dimension, the uniqueness of Karcher means is known to hold without further assumptions. A first counterexample where this uniqueness is not guaranteed is given in [Reference Álvarez-Esteban, del Barrio, Cuesta-Albertos and Matrán4]; see also the simplified Example 1. A general understanding of the uniqueness of Karcher means remains an open and interesting challenge, however. This is not only relevant for the present work, but also for the (non-stochastic) gradient descent method of [Reference Zemel and Panaretos55] and the fixed-point iterations of [Reference Álvarez-Esteban, del Barrio, Cuesta-Albertos and Matrán4]. The notion of pseudo-associativity introduced in Definition 4 provides an alternative viewpoint on this question, complementary to the aforementioned ones, which might deserve being further explored.
1.3. Gradient descents in Wasserstein space
Gradient descent (GD) in Wasserstein space was introduced as a method to compute barycenters in [Reference Álvarez-Esteban, del Barrio, Cuesta-Albertos and Matrán4, Reference Zemel and Panaretos55]. The SGD method we develop here was introduced in an early version of [Reference Backhoff-Veraguas, Fontbona, Rios and Tobar9] (arXiv:1805.10833) as a way to compute Bayesian estimators based on 2-Wasserstein barycenters. In view of the independent, theoretical interest of this SGD method, we decided to separately present this algorithm here, along with a deeper analysis and more complete results on it, and devote [Reference Backhoff-Veraguas, Fontbona, Rios and Tobar9] exclusively to its statistical application and implementation. More recently, [Reference Chewi, Maunu, Rigollet and Stromme19] obtained convergence rates for the expected optimality gap for these GD and SGD methods in the case of Gaussian families of distributions with uniformly bounded, uniformly positive-definite covariance matrices. This relied on proving a Polyak–Lojasiewicz inequality, and also derived quantitative convergence bounds in ![]() $W_2$ for the SGD sequence, relying on a variance inequality, which was shown to hold under general, though strong, conditions on the dual potential of the barycenter problem (verified under the assumptions in that paper). We refer to [Reference Carlier, Delalande and Merigot16] for more on the variance inequality.
$W_2$ for the SGD sequence, relying on a variance inequality, which was shown to hold under general, though strong, conditions on the dual potential of the barycenter problem (verified under the assumptions in that paper). We refer to [Reference Carlier, Delalande and Merigot16] for more on the variance inequality.
The Riemannian-like structure of the Wasserstein space and its associated gradient have been utilized in various other ways with statistical or machine learning motivations in recent years; see, e.g., [Reference Chizat and Bach21] for particle-like approximations, [Reference Kent, Li, Blanchet and Glynn34] for a sequential first-order method, and [Reference Chen and Li18, Reference Li and Montúfar39] for information geometry perspectives.
1.4. Computational aspects
Implementing our SGD algorithm requires, in general, computing or approximating optimal transport maps between two given absolutely continuous distributions (some exceptions where explicit closed-form maps are available are given in Section 6). During the last two decades, considerable progress has been made on the numerical resolution of the latter problem through partial differential equation methods [Reference Angenent, Haker and Tannenbaum7, Reference Benamou and Brenier10, Reference Bonneel, van de Panne, Paris and Heidrich14, Reference Loeper and Rapetti40] and, more recently, through entropic regularization approaches [Reference Cuturi25, Reference Cuturi and Peyré27, Reference Dognin29, Reference Mallasto, Gerolin and Minh41, Reference Peyré and Cuturi44, Reference Solomon49] crucially relying on the Sinkhorn algorithm [Reference Sinkhorn47, Reference Sinkhorn and Knopp48], which significantly speeds up the approximate resolution of the problem. It is also possible to approximate optimal transport maps via estimators built from samples (based on the Sinkhorn algorithm, plug-in estimators, or using stochastic approximations) [Reference Bercu and Bigot11, Reference Deb, Ghosal and Sen28, Reference Hütter and Rigollet33, Reference Manole, Balakrishnan, Niles-Weed and Wasserman42, Reference Pooladian and Niles-Weed45]. We also refer to [Reference Korotin37] for an overview and comparison of sample-free methods for continuous distributions, for instance based on neural networks (NNs).
1.5. Applications
The proposed method to compute Wasserstein barycenters is well suited to situations where a population law ![]() $\Pi$ on infinitely many probability measures is considered. The Bayesian setting addressed in [Reference Backhoff-Veraguas, Fontbona, Rios and Tobar9] provides a good example of such a situation, i.e. where we need to compute the Wasserstein barycenter of a prior/posterior distribution
$\Pi$ on infinitely many probability measures is considered. The Bayesian setting addressed in [Reference Backhoff-Veraguas, Fontbona, Rios and Tobar9] provides a good example of such a situation, i.e. where we need to compute the Wasserstein barycenter of a prior/posterior distribution ![]() $\Pi$ on models that has a possibly infinite support.
$\Pi$ on models that has a possibly infinite support.
Further instances of population laws ![]() $\Pi$ with infinite support arise in the context of Bayesian deep learning [Reference Wilson and Izmailov54], in which an NN’s weights are sampled from a given law (e.g. Gaussian, uniform, or Laplace); in the case that these NNs parametrize probability distributions, the collection of resulting probability laws is distributed according to a law
$\Pi$ with infinite support arise in the context of Bayesian deep learning [Reference Wilson and Izmailov54], in which an NN’s weights are sampled from a given law (e.g. Gaussian, uniform, or Laplace); in the case that these NNs parametrize probability distributions, the collection of resulting probability laws is distributed according to a law ![]() $\Pi$ with possibly infinite support. Another example is variational autoencoders [Reference Kingma and Welling36], which model the parameters of a law by a simple random variable (usually Gaussian) that is then passed to a decoder NN. In both cases, the support of
$\Pi$ with possibly infinite support. Another example is variational autoencoders [Reference Kingma and Welling36], which model the parameters of a law by a simple random variable (usually Gaussian) that is then passed to a decoder NN. In both cases, the support of ![]() $\Pi$ is infinite naturally. Furthermore, sampling from
$\Pi$ is infinite naturally. Furthermore, sampling from ![]() $\Pi$ is straightforward in these cases, which eases the implementation of the SGD algorithm.
$\Pi$ is straightforward in these cases, which eases the implementation of the SGD algorithm.
1.6. Possible extensions
It is in principle possible to define and study SGD methods similar to (2) for the minimization on the space of measures of other functionals than the barycentric objective function, or with respect to other geometries than the 2-Wasserstein one. For instance, [Reference Cazelles, Tobar and Fontbona17] introduces the notion of barycenters of probability measures based on weak optimal transport [Reference Backhoff-Veraguas, Beiglböck and Pammer8, Reference Gozlan and Juillet31, Reference Gozlan, Roberto, Samson and Tetali32] and extends the ideas and algorithm developed here to that setting. A further, natural, example of functionals to consider are the entropy-regularized barycenters dealt with for numerical purposes in some of the aforementioned works and most recently in [Reference Chizat20, Reference Chizat and Vaškevic̆ius22].
In a different vein, it would be interesting to study conditions ensuring the convergence of the algorithm in (2) to stationary points (Karcher means) when the latter is a class that strictly contains the minimum (barycenter). Under suitable conditions, such convergence can be expected to hold by analogy with the behavior of the Euclidean SGD algorithm in general (not necessarily convex) settings [Reference Bottou, Curtis and Nocedal15]. In fact, we believe this question can also be linked to the pseudo-associativity of Karcher means. A deeper study is left for future work.
2. Gradient descent in Wasserstein space: A review
We first survey the gradient descent method for the computation of 2-Wasserstein barycenters. This method will serve as motivation for the subsequent development of the SGD in Section 3. For simplicity, we take ![]() $\Pi$ to be finitely supported. Concretely, we suppose in this section that
$\Pi$ to be finitely supported. Concretely, we suppose in this section that ![]() $\Pi=\sum_{i\leq L}\lambda_i\delta_{m_i}$, with
$\Pi=\sum_{i\leq L}\lambda_i\delta_{m_i}$, with ![]() $L\in\mathbb{N}$,
$L\in\mathbb{N}$, ![]() $\lambda_i\geq 0$, and
$\lambda_i\geq 0$, and ![]() $\sum_{i\leq L}\lambda_i=1$. We define the operator over absolutely continuous measures
$\sum_{i\leq L}\lambda_i=1$. We define the operator over absolutely continuous measures
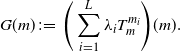 \begin{equation} G(m) \;:\!=\; \Bigg(\sum_{i=1}^{L}\lambda_iT_m^{m_i}\Bigg)(m).\end{equation}
\begin{equation} G(m) \;:\!=\; \Bigg(\sum_{i=1}^{L}\lambda_iT_m^{m_i}\Bigg)(m).\end{equation}
Notice that the fixed points of G are precisely the Karcher means of ![]() $\Pi$ presented in the introduction. Thanks to [Reference Álvarez-Esteban, del Barrio, Cuesta-Albertos and Matrán4] the operator G is continuous for the
$\Pi$ presented in the introduction. Thanks to [Reference Álvarez-Esteban, del Barrio, Cuesta-Albertos and Matrán4] the operator G is continuous for the ![]() ${W}_2$ distance. Also, if at least one of the L measures
${W}_2$ distance. Also, if at least one of the L measures ![]() $m_i$ has a bounded density, then the unique Wasserstein barycenter
$m_i$ has a bounded density, then the unique Wasserstein barycenter ![]() $\hat{m}$ of
$\hat{m}$ of ![]() $\Pi$ has a bounded density as well and satisfies
$\Pi$ has a bounded density as well and satisfies ![]() $G(\hat{m}) = \hat{m}$. This suggests defining, starting from
$G(\hat{m}) = \hat{m}$. This suggests defining, starting from ![]() $\mu_0$, the sequence
$\mu_0$, the sequence
The next result was proven in [Reference Álvarez-Esteban, del Barrio, Cuesta-Albertos and Matrán4, Theorem 3.6] and independently in [Reference Zemel and Panaretos55, Theorem 3, Corollary 2]:
Proposition 1. The sequence ![]() $\{\mu_n\}_{n \geq 0}$ in (7) is tight, and every weakly convergent subsequence of
$\{\mu_n\}_{n \geq 0}$ in (7) is tight, and every weakly convergent subsequence of ![]() $\{\mu_n\}_{n \geq 0}$ converges in
$\{\mu_n\}_{n \geq 0}$ converges in ![]() ${W}_2$ to an absolutely continuous measure in
${W}_2$ to an absolutely continuous measure in ![]() $\mathcal{W}_{2}(\mathbb{R}^q)$ that is also a Karcher mean. If some
$\mathcal{W}_{2}(\mathbb{R}^q)$ that is also a Karcher mean. If some ![]() $m_i$ has a bounded density, and if there exists a unique Karcher mean, then
$m_i$ has a bounded density, and if there exists a unique Karcher mean, then ![]() $\hat{m}$ is the Wasserstein barycenter of
$\hat{m}$ is the Wasserstein barycenter of ![]() $\Pi$ and
$\Pi$ and ![]() $W_2(\mu_n,\hat{m}) \rightarrow 0$.
$W_2(\mu_n,\hat{m}) \rightarrow 0$.
For the reader’s convenience, we present next a counterexample to the uniqueness of Karcher means.
Example 1. In ![]() $\mathbb R^2$ we take
$\mathbb R^2$ we take ![]() $\mu_1$ as the uniform measure on
$\mu_1$ as the uniform measure on ![]() $B((\!-\!1,M),\varepsilon)\cup B((1,-M),\varepsilon)$ and
$B((\!-\!1,M),\varepsilon)\cup B((1,-M),\varepsilon)$ and ![]() $\mu_2$ the uniform measure on
$\mu_2$ the uniform measure on ![]() $B((\!-\!1,-M),\varepsilon)\cup B((1,M),\varepsilon)$, with
$B((\!-\!1,-M),\varepsilon)\cup B((1,M),\varepsilon)$, with ![]() $\varepsilon$ a small radius and
$\varepsilon$ a small radius and ![]() $M\gg\varepsilon$. Then, if
$M\gg\varepsilon$. Then, if ![]() $\Pi=\frac{1}{2}(\delta_{\mu_1}+ \delta_{\mu_2})$, the uniform measure on
$\Pi=\frac{1}{2}(\delta_{\mu_1}+ \delta_{\mu_2})$, the uniform measure on ![]() $B((\!-\!1,0),\varepsilon)\cup B((1,0),\varepsilon)$ and the uniform measure on
$B((\!-\!1,0),\varepsilon)\cup B((1,0),\varepsilon)$ and the uniform measure on ![]() $B((0,M),\varepsilon)\cup B((0,-M),\varepsilon)$ are two distinct Karcher means.
$B((0,M),\varepsilon)\cup B((0,-M),\varepsilon)$ are two distinct Karcher means.
Thanks to the Riemann-like geometry of ![]() $\mathcal{W}_{2,\mathrm{ac}}(\mathbb{R}^q)$ we can reinterpret the iterations in (7) as a gradient descent step. This was discovered in [Reference Panaretos and Zemel43, Reference Zemel and Panaretos55]. In fact, [Reference Zemel and Panaretos55, Theorem 1] shows that the functional
$\mathcal{W}_{2,\mathrm{ac}}(\mathbb{R}^q)$ we can reinterpret the iterations in (7) as a gradient descent step. This was discovered in [Reference Panaretos and Zemel43, Reference Zemel and Panaretos55]. In fact, [Reference Zemel and Panaretos55, Theorem 1] shows that the functional
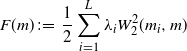 \begin{equation} F(m) \;:\!=\; \frac{1}{2}\sum_{i=1}^{L}\lambda_iW_2^2(m_i,m)\end{equation}
\begin{equation} F(m) \;:\!=\; \frac{1}{2}\sum_{i=1}^{L}\lambda_iW_2^2(m_i,m)\end{equation}
defined on ![]() $\mathcal{W}_2(\mathbb{R}^q)$ has a Fréchet derivative at each point
$\mathcal{W}_2(\mathbb{R}^q)$ has a Fréchet derivative at each point ![]() $m\in\mathcal{W}_{2,\mathrm{ac}}(\mathbb{R}^q)$ given by
$m\in\mathcal{W}_{2,\mathrm{ac}}(\mathbb{R}^q)$ given by
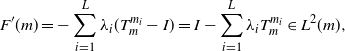 \begin{equation} F^\prime(m) = -\sum_{i=1}^{L}\lambda_i(T_m^{m_i}-I) = I-\sum_{i=1}^{L}\lambda_iT_m^{m_i} \in L^2(m),\end{equation}
\begin{equation} F^\prime(m) = -\sum_{i=1}^{L}\lambda_i(T_m^{m_i}-I) = I-\sum_{i=1}^{L}\lambda_iT_m^{m_i} \in L^2(m),\end{equation}
where I is the identity map in ![]() $\mathbb R^q$. More precisely, for such m, when
$\mathbb R^q$. More precisely, for such m, when ![]() $W_2(\hat{m},m)$ goes to zero,
$W_2(\hat{m},m)$ goes to zero,
thanks to [Reference Ambrosio, Gigli and Savaré6, Corollary 10.2.7]. It follows from Brenier’s theorem [Reference Villani50, Theorem 2.12(ii)] that ![]() $\hat{m}$ is a fixed point of G defined in (6) if and only if
$\hat{m}$ is a fixed point of G defined in (6) if and only if ![]() $F^\prime(\hat{m}) = 0$. The gradient descent sequence with step
$F^\prime(\hat{m}) = 0$. The gradient descent sequence with step ![]() $\gamma$ starting from
$\gamma$ starting from ![]() $\mu_0 \in \mathcal{W}_{2,\mathrm{ac}}(\mathbb{R}^q)$ is then defined by (cf. [Reference Zemel and Panaretos55])
$\mu_0 \in \mathcal{W}_{2,\mathrm{ac}}(\mathbb{R}^q)$ is then defined by (cf. [Reference Zemel and Panaretos55])
where
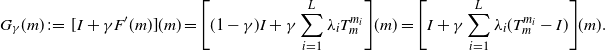 \begin{equation*} G_{\gamma}(m) \;:\!=\; [I + \gamma F^\prime(m)](m) = \Bigg[(1-\gamma)I + \gamma\sum_{i=1}^{L}\lambda_iT_m^{m_i}\Bigg](m) = \Bigg[I + \gamma\sum_{i=1}^{L}\lambda_i(T_m^{m_i}-I)\Bigg](m).\end{equation*}
\begin{equation*} G_{\gamma}(m) \;:\!=\; [I + \gamma F^\prime(m)](m) = \Bigg[(1-\gamma)I + \gamma\sum_{i=1}^{L}\lambda_iT_m^{m_i}\Bigg](m) = \Bigg[I + \gamma\sum_{i=1}^{L}\lambda_i(T_m^{m_i}-I)\Bigg](m).\end{equation*}
Note that, by (9), the iterations in (10) truly correspond to a gradient descent in ![]() $\mathcal{W}_2(\mathbb{R}^q)$ for the function in (8). We remark also that, if
$\mathcal{W}_2(\mathbb{R}^q)$ for the function in (8). We remark also that, if ![]() $\gamma=1$, the sequence in (10) coincides with that in (7), i.e.
$\gamma=1$, the sequence in (10) coincides with that in (7), i.e. ![]() $G_{1} = G$. These ideas serve as inspiration for the stochastic gradient descent iteration in the next part.
$G_{1} = G$. These ideas serve as inspiration for the stochastic gradient descent iteration in the next part.
3. Stochastic gradient descent for barycenters in Wasserstein space
The method presented in Section 2 is well suited to calculating the empirical barycenter. For the estimation of a population barycenter (i.e. when ![]() $\Pi$ does not have finite support) we would need to construct a convergent sequence of empirical barycenters, which can be computationally expensive. Furthermore, if a new sample from
$\Pi$ does not have finite support) we would need to construct a convergent sequence of empirical barycenters, which can be computationally expensive. Furthermore, if a new sample from ![]() $\Pi$ arrives, the previous method would need to recalculate the barycenter from scratch. To address these challenges, we follow the ideas of stochastic algorithms [Reference Robbins and Monro46], widely adopted in machine learning [Reference Bottou, Curtis and Nocedal15], and define a stochastic version of the gradient descent sequence for the barycenter of
$\Pi$ arrives, the previous method would need to recalculate the barycenter from scratch. To address these challenges, we follow the ideas of stochastic algorithms [Reference Robbins and Monro46], widely adopted in machine learning [Reference Bottou, Curtis and Nocedal15], and define a stochastic version of the gradient descent sequence for the barycenter of ![]() $\Pi$.
$\Pi$.
Recall that for ![]() $\mu_0 \in K_\Pi$ (in particular,
$\mu_0 \in K_\Pi$ (in particular, ![]() $\mu_0$ absolutely continuous),
$\mu_0$ absolutely continuous), ![]() $m_k \stackrel{\text{i.i.d.}}{\sim} \Pi$ defined in some probability space
$m_k \stackrel{\text{i.i.d.}}{\sim} \Pi$ defined in some probability space ![]() $(\Omega, \mathcal{F}, \mathbb{P})$, and
$(\Omega, \mathcal{F}, \mathbb{P})$, and ![]() $\gamma_k > 0$ for
$\gamma_k > 0$ for ![]() $k \geq 0$, we constructed the SGD sequence as
$k \geq 0$, we constructed the SGD sequence as ![]() $\mu_{k+1} \;:\!=\; \big[(1-\gamma_k)I + \gamma_k T_{\mu_k}^{m_k}\big](\mu_k)$ for
$\mu_{k+1} \;:\!=\; \big[(1-\gamma_k)I + \gamma_k T_{\mu_k}^{m_k}\big](\mu_k)$ for ![]() $k \geq 0$. The key ingredients for the convergence analysis of the above SGD iterations are the functions
$k \geq 0$. The key ingredients for the convergence analysis of the above SGD iterations are the functions
the natural analogues to the eponymous objects in (8) and (9). In this setting, we can formally (or rigorously, under additional assumptions) check that F ′ is the actual Frechet derivative of F, and this justifies naming ![]() $\{\mu_k\}_k$ a SGD sequence. In the following, the notation F and F ′ always refers to the functions just defined. Observe that the population barycenter
$\{\mu_k\}_k$ a SGD sequence. In the following, the notation F and F ′ always refers to the functions just defined. Observe that the population barycenter ![]() $\hat \mu$ is the unique minimizer of F. The following lemma justifies that F ′ is well defined and that
$\hat \mu$ is the unique minimizer of F. The following lemma justifies that F ′ is well defined and that ![]() $\|F'(\hat\mu)\|_{L^2(\hat \mu)}=0$, and in particular that
$\|F'(\hat\mu)\|_{L^2(\hat \mu)}=0$, and in particular that ![]() $\hat \mu$ is a Karcher mean. This is a generalization of the corresponding result in [Reference Álvarez-Esteban, del Barrio, Cuesta-Albertos and Matrán4] where only the case
$\hat \mu$ is a Karcher mean. This is a generalization of the corresponding result in [Reference Álvarez-Esteban, del Barrio, Cuesta-Albertos and Matrán4] where only the case ![]() $|\text{supp}(\Pi)|<\infty$ is covered.
$|\text{supp}(\Pi)|<\infty$ is covered.
Lemma 1. Let ![]() $\tilde\Pi$ be a probability measure concentrated on
$\tilde\Pi$ be a probability measure concentrated on ![]() $\mathcal W_{2,\mathrm{ac}}(\mathbb R^q)$. There exists a jointly measurable function
$\mathcal W_{2,\mathrm{ac}}(\mathbb R^q)$. There exists a jointly measurable function ![]() $\mathcal W_{2,\mathrm{ac}}(\mathbb R^q)\times\mathcal W_2(\mathbb R^q)\times\mathbb R^q \ni (\mu,m,x) \mapsto T^m_\mu(x)$ that is
$\mathcal W_{2,\mathrm{ac}}(\mathbb R^q)\times\mathcal W_2(\mathbb R^q)\times\mathbb R^q \ni (\mu,m,x) \mapsto T^m_\mu(x)$ that is ![]() $\mu({\mathrm{d}} x)\,\Pi({\mathrm{d}} m)\,\tilde\Pi({\mathrm{d}}\mu)$-a.s. equal to the unique optimal transport map from
$\mu({\mathrm{d}} x)\,\Pi({\mathrm{d}} m)\,\tilde\Pi({\mathrm{d}}\mu)$-a.s. equal to the unique optimal transport map from ![]() $\mu$ to m at x. Furthermore, letting
$\mu$ to m at x. Furthermore, letting ![]() $\hat\mu$ be a barycenter of
$\hat\mu$ be a barycenter of ![]() $\Pi$,
$\Pi$, ![]() $x = \int T^m_{\hat\mu}(x)\,\Pi({\mathrm{d}} m),$
$x = \int T^m_{\hat\mu}(x)\,\Pi({\mathrm{d}} m),$ ![]() $\hat\mu({\mathrm{d}} x)$-a.s.
$\hat\mu({\mathrm{d}} x)$-a.s.
Proof. The existence of a jointly measurable version of the unique optimal maps is proved in [Reference Fontbona, Guérin and Méléard30]. Let us prove the last assertion. Letting ![]() $T^m_{\hat\mu}\;=\!:\;T^m$, we have, by Brenier’s theorem [Reference Villani50, Theorem 2.12(ii)],
$T^m_{\hat\mu}\;=\!:\;T^m$, we have, by Brenier’s theorem [Reference Villani50, Theorem 2.12(ii)],
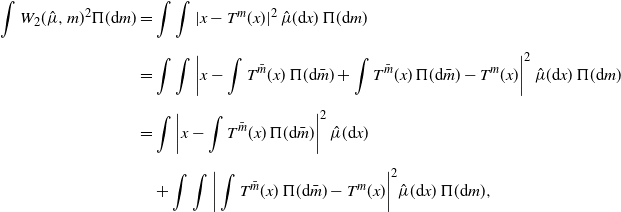 \begin{align*} \int W_2(\hat\mu,m)^2\Pi({\mathrm{d}} m) & = \int\int|x-T^m(x)|^2\,\hat\mu({\mathrm{d}} x)\,\Pi({\mathrm{d}} m) \\[5pt] & = \int\int\bigg|x-\int T^{\bar m}(x)\,\Pi({\mathrm{d}}{\bar m}) + \int T^{\bar m}(x)\,\Pi({\mathrm{d}}{\bar m}) - T^m(x)\bigg|^2\,\hat\mu({\mathrm{d}} x)\,\Pi({\mathrm{d}} m) \\[5pt] & = \int\bigg|x-\int T^{\bar m}(x)\,\Pi({\mathrm{d}}{\bar m})\bigg|^2\,\hat\mu({\mathrm{d}} x) \\[5pt] & \quad + \int\int\bigg|\int T^{\bar m}(x)\,\Pi({\mathrm{d}}{\bar m}) - T^m(x)\bigg|^2\hat\mu({\mathrm{d}} x)\,\Pi({\mathrm{d}} m), \end{align*}
\begin{align*} \int W_2(\hat\mu,m)^2\Pi({\mathrm{d}} m) & = \int\int|x-T^m(x)|^2\,\hat\mu({\mathrm{d}} x)\,\Pi({\mathrm{d}} m) \\[5pt] & = \int\int\bigg|x-\int T^{\bar m}(x)\,\Pi({\mathrm{d}}{\bar m}) + \int T^{\bar m}(x)\,\Pi({\mathrm{d}}{\bar m}) - T^m(x)\bigg|^2\,\hat\mu({\mathrm{d}} x)\,\Pi({\mathrm{d}} m) \\[5pt] & = \int\bigg|x-\int T^{\bar m}(x)\,\Pi({\mathrm{d}}{\bar m})\bigg|^2\,\hat\mu({\mathrm{d}} x) \\[5pt] & \quad + \int\int\bigg|\int T^{\bar m}(x)\,\Pi({\mathrm{d}}{\bar m}) - T^m(x)\bigg|^2\hat\mu({\mathrm{d}} x)\,\Pi({\mathrm{d}} m), \end{align*}
where we used the fact that
The term in the last line is an upper bound for
We conclude that ![]() $\int\big|x-\int T^{\bar m}(x)\,\Pi({\mathrm{d}}{\bar m})\big|^2\,\hat\mu({\mathrm{d}} x)$, as required.
$\int\big|x-\int T^{\bar m}(x)\,\Pi({\mathrm{d}}{\bar m})\big|^2\,\hat\mu({\mathrm{d}} x)$, as required.
Notice that Lemma 1 ensures that the SGD sequence ![]() $\{\mu_k\}_k$ is well defined as a sequence of (measurable)
$\{\mu_k\}_k$ is well defined as a sequence of (measurable) ![]() $\mathcal{W}_2$-valued random variables. More precisely, denoting by
$\mathcal{W}_2$-valued random variables. More precisely, denoting by ![]() $\mathcal F_{0}$ the trivial sigma-algebra and
$\mathcal F_{0}$ the trivial sigma-algebra and ![]() $\mathcal F_{k+1}$,
$\mathcal F_{k+1}$, ![]() $k\geq 0$, the sigma-algebra generated by
$k\geq 0$, the sigma-algebra generated by ![]() $m_0,\dots,m_{k}$, we can inductively apply the first part of Lemma 1 with
$m_0,\dots,m_{k}$, we can inductively apply the first part of Lemma 1 with ![]() $\tilde{\Pi}=\mathrm{Law}(\mu_{k})$ to check that
$\tilde{\Pi}=\mathrm{Law}(\mu_{k})$ to check that ![]() $T_{\mu_k}^{m_k}(x)$ is measurable with respect to
$T_{\mu_k}^{m_k}(x)$ is measurable with respect to ![]() $\mathcal F_{k+1}\otimes \mathcal B (\mathbb{R}^q)$, where
$\mathcal F_{k+1}\otimes \mathcal B (\mathbb{R}^q)$, where ![]() $\mathcal B$ stands for the Borel sigma-field. This implies that both
$\mathcal B$ stands for the Borel sigma-field. This implies that both ![]() $\mu_{k}$ and
$\mu_{k}$ and ![]() $\|F^\prime(\mu_{k})\|^2_{L^2(\mu_{k})}$ are measurable with respect to
$\|F^\prime(\mu_{k})\|^2_{L^2(\mu_{k})}$ are measurable with respect to ![]() $\mathcal F_{k}$.
$\mathcal F_{k}$.
The next proposition suggests that, in expectation, the sequence ![]() $\{F(\mu_k)\}_k$ is essentially decreasing. This is a first insight into the behavior of the sequence
$\{F(\mu_k)\}_k$ is essentially decreasing. This is a first insight into the behavior of the sequence ![]() $\{\mu_k\}_k$.
$\{\mu_k\}_k$.
Proposition 2. The SGD sequence in (2) satisfies, almost surely,
Proof. Let ![]() $\nu\in\text{supp}(\Pi)$. Clearly,
$\nu\in\text{supp}(\Pi)$. Clearly, ![]() $\big(\big[(1-\gamma_k)I + \gamma_k T_{\mu_k}^{m_k}\big],T_{\mu_k}^\nu\big)(\mu_k)$ is a feasible (not necessarily optimal) coupling with first and second marginals
$\big(\big[(1-\gamma_k)I + \gamma_k T_{\mu_k}^{m_k}\big],T_{\mu_k}^\nu\big)(\mu_k)$ is a feasible (not necessarily optimal) coupling with first and second marginals ![]() $\mu_{k+1}$ and
$\mu_{k+1}$ and ![]() $\nu$ respectively. Writing
$\nu$ respectively. Writing ![]() $O_m\;:\!=\; T_{\mu_k}^{m} - I$, we have
$O_m\;:\!=\; T_{\mu_k}^{m} - I$, we have
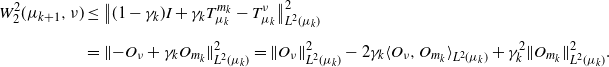 \begin{align*} W_2^2(\mu_{k+1},\nu) & \leq \big\|(1-\gamma_k)I + \gamma_k T_{\mu_k}^{m_k} - T_{\mu_k}^{\nu}\big\|^2_{L^2(\mu_k)} \\[5pt] & = \|{-}O_{\nu} + \gamma_k O_{m_k}\|^2_{L^2(\mu_k)} = \|O_{\nu}\|^2_{L^2(\mu_k)} - 2\gamma_k\langle O_{\nu},O_{m_k}\rangle_{L^2(\mu_k)} + \gamma_k^2\|O_{m_k}\|^2_{L^2(\mu_k)}. \end{align*}
\begin{align*} W_2^2(\mu_{k+1},\nu) & \leq \big\|(1-\gamma_k)I + \gamma_k T_{\mu_k}^{m_k} - T_{\mu_k}^{\nu}\big\|^2_{L^2(\mu_k)} \\[5pt] & = \|{-}O_{\nu} + \gamma_k O_{m_k}\|^2_{L^2(\mu_k)} = \|O_{\nu}\|^2_{L^2(\mu_k)} - 2\gamma_k\langle O_{\nu},O_{m_k}\rangle_{L^2(\mu_k)} + \gamma_k^2\|O_{m_k}\|^2_{L^2(\mu_k)}. \end{align*}
Evaluating ![]() $\mu_{k+1}$ on the functional F, thanks to the previous inequality we have
$\mu_{k+1}$ on the functional F, thanks to the previous inequality we have
 \begin{align*} F(\mu_{k+1}) & = \frac{1}{2}\int W_{2}^2(\mu_{k+1},\nu)\,\Pi({\mathrm{d}}\nu) \\[5pt] & \leq \frac{1}{2}\int\|O_{\nu}\|^2_{L^2(\mu_k)}\,\Pi({\mathrm{d}}\nu) - \gamma_k\bigg\langle\int O_{\nu}\,\Pi({\mathrm{d}}\nu),O_{m_k}\bigg\rangle_{L^2(\mu_k)} + \frac{\gamma_k^2}{2}\|O_{m_k}\|^2_{L^2(\mu_k)} \\[5pt] & = F(\mu_k) + \gamma_k\langle F^\prime(\mu_k),O_{m_k}\rangle_{L^2(\mu_k)} + \frac{\gamma_k^2}{2}\|O_{m_k}\|^2_{L^2(\mu_k)}. \end{align*}
\begin{align*} F(\mu_{k+1}) & = \frac{1}{2}\int W_{2}^2(\mu_{k+1},\nu)\,\Pi({\mathrm{d}}\nu) \\[5pt] & \leq \frac{1}{2}\int\|O_{\nu}\|^2_{L^2(\mu_k)}\,\Pi({\mathrm{d}}\nu) - \gamma_k\bigg\langle\int O_{\nu}\,\Pi({\mathrm{d}}\nu),O_{m_k}\bigg\rangle_{L^2(\mu_k)} + \frac{\gamma_k^2}{2}\|O_{m_k}\|^2_{L^2(\mu_k)} \\[5pt] & = F(\mu_k) + \gamma_k\langle F^\prime(\mu_k),O_{m_k}\rangle_{L^2(\mu_k)} + \frac{\gamma_k^2}{2}\|O_{m_k}\|^2_{L^2(\mu_k)}. \end{align*}
Taking conditional expectation with respect to ![]() $\mathcal F_k$, and as
$\mathcal F_k$, and as ![]() $m_k$ is independently sampled from this sigma-algebra, we conclude that
$m_k$ is independently sampled from this sigma-algebra, we conclude that
 \begin{align*} \mathbb{E}[F(\mu_{k+1})\mid\mathcal F_k] & \leq F(\mu_k) + \gamma_k\bigg\langle F^\prime(\mu_k),\int O_{m}\,\Pi({\mathrm{d}} m)\bigg\rangle_{L^2(\mu_k)} + \frac{\gamma_k^2}{2}\int\lVert |O_{m}\rVert^2_{L^2(\mu_k)}\,\Pi({\mathrm{d}} m) \\[5pt] & = (1+\gamma_k^2)F(\mu_k) - \gamma_k\|F^\prime(\mu_k)\|^2_{L^2(\mu_k)}. \end{align*}
\begin{align*} \mathbb{E}[F(\mu_{k+1})\mid\mathcal F_k] & \leq F(\mu_k) + \gamma_k\bigg\langle F^\prime(\mu_k),\int O_{m}\,\Pi({\mathrm{d}} m)\bigg\rangle_{L^2(\mu_k)} + \frac{\gamma_k^2}{2}\int\lVert |O_{m}\rVert^2_{L^2(\mu_k)}\,\Pi({\mathrm{d}} m) \\[5pt] & = (1+\gamma_k^2)F(\mu_k) - \gamma_k\|F^\prime(\mu_k)\|^2_{L^2(\mu_k)}. \end{align*}
The next lemma states some key continuity properties of the functions F and F ′. For this result, Assumption 2 can be dropped and it is only required that ![]() $\int\int\|x\|^2\,m({\mathrm{d}} x)\,\Pi({\mathrm{d}} m)<\infty$.
$\int\int\|x\|^2\,m({\mathrm{d}} x)\,\Pi({\mathrm{d}} m)<\infty$.
Lemma 2. Let ![]() $(\rho_n)_n\subset\mathcal{W}_{2,\mathrm{ac}}(\mathbb{R}^q)$ be a sequence converging with respect to
$(\rho_n)_n\subset\mathcal{W}_{2,\mathrm{ac}}(\mathbb{R}^q)$ be a sequence converging with respect to ![]() $W_2$ to
$W_2$ to ![]() $\rho\in\mathcal{W}_{2,\mathrm{ac}}(\mathbb{R}^q)$. Then, as
$\rho\in\mathcal{W}_{2,\mathrm{ac}}(\mathbb{R}^q)$. Then, as ![]() $n\to\infty$,
$n\to\infty$,
(i)
 $F(\rho_n)\to F(\rho)$;
$F(\rho_n)\to F(\rho)$;-
(ii)
 $\|F'(\rho_n)\|_{L^2(\rho_n)}\to\|F'(\rho)\|_{L^2(\rho)}$.
$\|F'(\rho_n)\|_{L^2(\rho_n)}\to\|F'(\rho)\|_{L^2(\rho)}$.
Proof. We prove both convergence claims using Skorokhod’s representation theorem. Thanks to that result, in a given probability space ![]() $(\Omega,\mathcal{G},{\mathbb{P}})$ we can simultaneously construct a sequence of random vectors
$(\Omega,\mathcal{G},{\mathbb{P}})$ we can simultaneously construct a sequence of random vectors ![]() $(X_n)_n$ of laws
$(X_n)_n$ of laws ![]() $(\rho_n)_n$ and a random variable X of law
$(\rho_n)_n$ and a random variable X of law ![]() $\rho$ such that
$\rho$ such that ![]() $(X_n)_n$ converges
$(X_n)_n$ converges ![]() ${\mathbb{P}}$-a.s. to X. Moreover, by [Reference Cuesta-Albertos, Matrán and Tuero-Diaz23, Theorem 3.4], the sequence
${\mathbb{P}}$-a.s. to X. Moreover, by [Reference Cuesta-Albertos, Matrán and Tuero-Diaz23, Theorem 3.4], the sequence ![]() $(T_{\rho_n}^m(X_n))_n$ converges
$(T_{\rho_n}^m(X_n))_n$ converges ![]() ${\mathbb{P}}$-a.s. to
${\mathbb{P}}$-a.s. to ![]() $T_{\rho}^m(X)$. Notice that, for all
$T_{\rho}^m(X)$. Notice that, for all ![]() $n\in\mathbb{N}$,
$n\in\mathbb{N}$, ![]() $T_{\rho_n}^m(X_n)$ distributes according to the law m, and the same holds true for
$T_{\rho_n}^m(X_n)$ distributes according to the law m, and the same holds true for ![]() $T_{\rho}^m(X)$.
$T_{\rho}^m(X)$.
We now enlarge the probability space ![]() $(\Omega,\mathcal{G},{\mathbb{P}})$ (maintaining the same notation for simplicity) with an independent random variable
$(\Omega,\mathcal{G},{\mathbb{P}})$ (maintaining the same notation for simplicity) with an independent random variable ![]() $\textbf{m}$ in
$\textbf{m}$ in ![]() $\mathcal{W}_2(\mathbb{R}^d)$ with law
$\mathcal{W}_2(\mathbb{R}^d)$ with law ![]() $\Pi$ (thus independent of
$\Pi$ (thus independent of ![]() $(X_n)_n$ and X). Applying Lemma 1 with
$(X_n)_n$ and X). Applying Lemma 1 with ![]() $\tilde{\Pi}=\delta_{\rho_n}$ for each n, or with
$\tilde{\Pi}=\delta_{\rho_n}$ for each n, or with ![]() $\tilde{\Pi}=\delta_{\rho}$, we can show that
$\tilde{\Pi}=\delta_{\rho}$, we can show that ![]() $\big(X_n,T_{\rho_n}^{\textbf{m}}(X_n)\big)$ and
$\big(X_n,T_{\rho_n}^{\textbf{m}}(X_n)\big)$ and ![]() $\big(X,T_{\rho}^{\textbf{m}}(X)\big)$ are random variables in
$\big(X,T_{\rho}^{\textbf{m}}(X)\big)$ are random variables in ![]() $(\Omega,\mathcal{G},{\mathbb{P}})$. By conditioning on
$(\Omega,\mathcal{G},{\mathbb{P}})$. By conditioning on ![]() $\{\textbf{m}=m\}$, we further obtain that
$\{\textbf{m}=m\}$, we further obtain that ![]() $\big(X_n,T_{\rho_n}^{\textbf{m}}(X_n)\big)_{n\in\mathbb{N}}$ converges
$\big(X_n,T_{\rho_n}^{\textbf{m}}(X_n)\big)_{n\in\mathbb{N}}$ converges ![]() ${\mathbb{P}}$-a.s. to
${\mathbb{P}}$-a.s. to ![]() $\big(X,T_{\rho}^{\textbf{m}}(X)\big)$.
$\big(X,T_{\rho}^{\textbf{m}}(X)\big)$.
Notice that ![]() $\sup_n\mathbb{E}\big(\|X_n\|^2\textbf{1}_{\|X_n\|^2\geq M}\big) = \sup_n\int_{\|x\|^2\geq M}\|x\|^2\,\rho_n({\mathrm{d}} x) \to 0$ as
$\sup_n\mathbb{E}\big(\|X_n\|^2\textbf{1}_{\|X_n\|^2\geq M}\big) = \sup_n\int_{\|x\|^2\geq M}\|x\|^2\,\rho_n({\mathrm{d}} x) \to 0$ as ![]() $M\to\infty$ since
$M\to\infty$ since ![]() $(\rho_n)_n$ converges in
$(\rho_n)_n$ converges in ![]() $\mathcal{W}_2(\mathcal{X})$, while, upon conditioning on
$\mathcal{W}_2(\mathcal{X})$, while, upon conditioning on ![]() $\textbf{m}$,
$\textbf{m}$,
by dominated convergence, since ![]() $\int_{\|x\|^2\geq M}\|x\|^2\,m({\mathrm{d}} x)\leq\int\|x\|^2\,m({\mathrm{d}} x) = W_2^2(m,\delta_0)$ and
$\int_{\|x\|^2\geq M}\|x\|^2\,m({\mathrm{d}} x)\leq\int\|x\|^2\,m({\mathrm{d}} x) = W_2^2(m,\delta_0)$ and ![]() $\Pi\in\mathcal{W}_2(\mathcal{W}_2(\mathcal{X}))$. By Vitalli’s convergence theorem, we deduce that
$\Pi\in\mathcal{W}_2(\mathcal{W}_2(\mathcal{X}))$. By Vitalli’s convergence theorem, we deduce that ![]() $(X_n,T_{\rho_n}^{\textbf{m}}(X_n))_{n\in\mathbb{N}}$ converges to
$(X_n,T_{\rho_n}^{\textbf{m}}(X_n))_{n\in\mathbb{N}}$ converges to ![]() $(X,T_{\rho}^{\textbf{m}}(X))$ in
$(X,T_{\rho}^{\textbf{m}}(X))$ in ![]() $L^2(\Omega,\mathcal{G},{\mathbb{P}})$. In particular, as
$L^2(\Omega,\mathcal{G},{\mathbb{P}})$. In particular, as ![]() $n\to \infty$,
$n\to \infty$,
which proves the convergence in (i). Now denoting by ![]() $\mathcal{G}_{\infty}$ the sigma-field generated by
$\mathcal{G}_{\infty}$ the sigma-field generated by ![]() $(X_1,X_2,\dots)$, we also obtain that
$(X_1,X_2,\dots)$, we also obtain that
Observe now that the following identities hold:
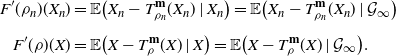 \begin{align*} F'(\rho_n)(X_n) & = \mathbb{E}\big(X_n-T_{\rho_n}^{\textbf{m}}(X_n)\mid X_n\big) = \mathbb{E}\big(X_n-T_{\rho_n}^{\textbf{m}}(X_n)\mid\mathcal{G}_{\infty}\big) \\[5pt] F'(\rho)(X) & = \mathbb{E}\big(X-T_{\rho}^{\textbf{m}}(X)\mid X\big) = \mathbb{E}\big(X-T_{\rho}^{\textbf{m}}(X)\mid\mathcal{G}_{\infty}\big). \end{align*}
\begin{align*} F'(\rho_n)(X_n) & = \mathbb{E}\big(X_n-T_{\rho_n}^{\textbf{m}}(X_n)\mid X_n\big) = \mathbb{E}\big(X_n-T_{\rho_n}^{\textbf{m}}(X_n)\mid\mathcal{G}_{\infty}\big) \\[5pt] F'(\rho)(X) & = \mathbb{E}\big(X-T_{\rho}^{\textbf{m}}(X)\mid X\big) = \mathbb{E}\big(X-T_{\rho}^{\textbf{m}}(X)\mid\mathcal{G}_{\infty}\big). \end{align*}
The convergence in (ii) follows from (12), ![]() $\mathbb{E}(F'(\rho_n)(X_n))^2 = \|F'(\rho_n)\|_{L^2(\rho_n)}$, and
$\mathbb{E}(F'(\rho_n)(X_n))^2 = \|F'(\rho_n)\|_{L^2(\rho_n)}$, and ![]() $\mathbb{E}(F'(\rho)(X))^2 = \|F'(\rho)\|_{L^2(\rho)}$.
$\mathbb{E}(F'(\rho)(X))^2 = \|F'(\rho)\|_{L^2(\rho)}$.
We now proceed to prove the first of our two main results.
Proof of Theorem 1. Let us denote by ![]() $\hat\mu$ the unique barycenter, write
$\hat\mu$ the unique barycenter, write ![]() $\hat{F} \;:\!=\; F(\hat{\mu})$, and introduce
$\hat{F} \;:\!=\; F(\hat{\mu})$, and introduce ![]() $h_t \;:\!=\; F(\mu_t) - \hat{F} \geq 0$ and
$h_t \;:\!=\; F(\mu_t) - \hat{F} \geq 0$ and ![]() $\alpha_t \;:\!=\; \prod_{i=1}^{t-1}{1}/({1+\gamma_i^2})$. Thanks to the condition in (3), the sequence
$\alpha_t \;:\!=\; \prod_{i=1}^{t-1}{1}/({1+\gamma_i^2})$. Thanks to the condition in (3), the sequence ![]() $(\alpha_t)$ converges to some finite
$(\alpha_t)$ converges to some finite ![]() $\alpha_\infty>0$, as can be verified simply by applying logarithms. By Proposition 2,
$\alpha_\infty>0$, as can be verified simply by applying logarithms. By Proposition 2,
from which, after multiplying by ![]() $\alpha_{t+1}$, the following bound is derived:
$\alpha_{t+1}$, the following bound is derived:
Now defining ![]() $\hat{h}_t\;:\!=\; \alpha_t h_t - \sum_{i=1}^{t}\alpha_i\gamma_{i-1}^2\hat{F}$, we deduce from (13) that
$\hat{h}_t\;:\!=\; \alpha_t h_t - \sum_{i=1}^{t}\alpha_i\gamma_{i-1}^2\hat{F}$, we deduce from (13) that ![]() $\mathbb{E}[\hat{h}_{t+1}-\hat{h}_t\mid\mathcal F_t] \leq 0$, namely that
$\mathbb{E}[\hat{h}_{t+1}-\hat{h}_t\mid\mathcal F_t] \leq 0$, namely that ![]() $(\hat{h}_t)_{t\geq 0}$ is a supermartingale with respect to
$(\hat{h}_t)_{t\geq 0}$ is a supermartingale with respect to ![]() $(\mathcal F_t)$. The fact that
$(\mathcal F_t)$. The fact that ![]() $(\alpha_t)$ is convergent, together with the condition in (3), ensures that
$(\alpha_t)$ is convergent, together with the condition in (3), ensures that ![]() $\sum_{i=1}^{\infty}\alpha_i\gamma_{i-1}^2\hat{F}<\infty$, and thus
$\sum_{i=1}^{\infty}\alpha_i\gamma_{i-1}^2\hat{F}<\infty$, and thus ![]() $\hat{h}_t$ is uniformly lower-bounded by a constant. Therefore, the supermartingale convergence theorem [Reference Williams53, Corollary 11.7] implies the existence of
$\hat{h}_t$ is uniformly lower-bounded by a constant. Therefore, the supermartingale convergence theorem [Reference Williams53, Corollary 11.7] implies the existence of ![]() $\hat{h}_{\infty}\in L^1$ such that
$\hat{h}_{\infty}\in L^1$ such that ![]() $\hat{h}_t\to \hat{h}_{\infty}$ a.s. But then, necessarily,
$\hat{h}_t\to \hat{h}_{\infty}$ a.s. But then, necessarily, ![]() $h_t\to h_{\infty}$ a.s. for some non-negative random variable
$h_t\to h_{\infty}$ a.s. for some non-negative random variable ![]() $h_{\infty}\in L^1$.
$h_{\infty}\in L^1$.
Thus, our goal now is to prove that ![]() $h_{\infty}=0$ a.s. Taking expectations in (13) and summing over t to obtain a telescopic summation, we obtain
$h_{\infty}=0$ a.s. Taking expectations in (13) and summing over t to obtain a telescopic summation, we obtain
Then, taking liminf, applying Fatou on the left-hand side and monotone convergence on the right-hand side, we obtain
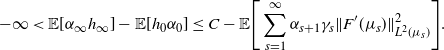 $$ -\infty
< \mathbb E[\alpha_{\infty}h_{\infty}] - \mathbb{E}[h_0\alpha_0] \leq C - \mathbb E\Bigg[\sum_{s=1}^\infty\alpha_{s+1}\gamma_s\|F^\prime(\mu_s)\|^2_{L^2(\mu_s)}\Bigg]. $$
$$ -\infty
< \mathbb E[\alpha_{\infty}h_{\infty}] - \mathbb{E}[h_0\alpha_0] \leq C - \mathbb E\Bigg[\sum_{s=1}^\infty\alpha_{s+1}\gamma_s\|F^\prime(\mu_s)\|^2_{L^2(\mu_s)}\Bigg]. $$
In particular, since ![]() $(\alpha_t)$ is bounded away from 0, we have
$(\alpha_t)$ is bounded away from 0, we have
Note that ![]() ${\mathbb{P}}(\liminf_{t\to \infty}\|F^\prime(\mu_t)\|^2_{L^2(\mu_t)}>0)>0$ would be at odds with the conditions in (14) and (4), so
${\mathbb{P}}(\liminf_{t\to \infty}\|F^\prime(\mu_t)\|^2_{L^2(\mu_t)}>0)>0$ would be at odds with the conditions in (14) and (4), so
Observe also that, from Assumption 2 and Lemma 2, we have
Indeed, we can see that the set ![]() $\{\rho\colon F(\rho) \geq \hat F + \varepsilon\}\cap K_\Pi$ is
$\{\rho\colon F(\rho) \geq \hat F + \varepsilon\}\cap K_\Pi$ is ![]() $W_2$-compact, using Lemma 2(i), and then check that the function
$W_2$-compact, using Lemma 2(i), and then check that the function ![]() $\rho\mapsto\|F^\prime(\rho)\|^2_{L^2(\rho)}$ attains its minimum on it, using part (ii) of that result. That minimum cannot be zero, as otherwise we would have obtained a Karcher mean that is not equal to the barycenter (contradicting the uniqueness of the Karcher mean). Note also that, a.s.,
$\rho\mapsto\|F^\prime(\rho)\|^2_{L^2(\rho)}$ attains its minimum on it, using part (ii) of that result. That minimum cannot be zero, as otherwise we would have obtained a Karcher mean that is not equal to the barycenter (contradicting the uniqueness of the Karcher mean). Note also that, a.s., ![]() $\mu_t\in K_\Pi$ for each t, by the geodesic convexity part of Assumption 2. We deduce the following a.s. relationships between events:
$\mu_t\in K_\Pi$ for each t, by the geodesic convexity part of Assumption 2. We deduce the following a.s. relationships between events:
 \begin{align*} \{h_{\infty} \geq 2\varepsilon\} & \subset\{\mu_t\in\{\rho\colon F(\rho) \geq \hat F + \varepsilon\} \cap K_\Pi \text{ for all } t \mbox{ large enough} \} \\[5pt] & \subset \bigcup_{\ell\in\mathbb{N}}\big\{\|F^\prime(\mu_t)\|^2_{L^2(\mu_t)} > 1/\ell\colon \text{for all } t \mbox{ large enough}\big\} \\[5pt] & \subset \Big\{\liminf_{t\to\infty}\|F^\prime(\mu_t)\|^2_{L^2(\mu_t)}>0\Big\}, \end{align*}
\begin{align*} \{h_{\infty} \geq 2\varepsilon\} & \subset\{\mu_t\in\{\rho\colon F(\rho) \geq \hat F + \varepsilon\} \cap K_\Pi \text{ for all } t \mbox{ large enough} \} \\[5pt] & \subset \bigcup_{\ell\in\mathbb{N}}\big\{\|F^\prime(\mu_t)\|^2_{L^2(\mu_t)} > 1/\ell\colon \text{for all } t \mbox{ large enough}\big\} \\[5pt] & \subset \Big\{\liminf_{t\to\infty}\|F^\prime(\mu_t)\|^2_{L^2(\mu_t)}>0\Big\}, \end{align*}
where (16) was used to obtain the second inclusion. It follows using (15) that ![]() ${\mathbb{P}}(h_{\infty}\geq2\varepsilon)=0$ for every
${\mathbb{P}}(h_{\infty}\geq2\varepsilon)=0$ for every ![]() $\varepsilon>0$, and hence
$\varepsilon>0$, and hence ![]() $h_{\infty}=0$ as required.
$h_{\infty}=0$ as required.
To conclude, we use the fact that the sequence ![]() $\{\mu_t\}_t$ is a.s. contained in the
$\{\mu_t\}_t$ is a.s. contained in the ![]() $W_2$-compact
$W_2$-compact ![]() $K_\Pi$ by Assumption 2, and the first convergence in Lemma 2 to deduce that the limit
$K_\Pi$ by Assumption 2, and the first convergence in Lemma 2 to deduce that the limit ![]() $\tilde{\mu}$ of any convergent subsequence satisfies
$\tilde{\mu}$ of any convergent subsequence satisfies ![]() $F(\tilde{\mu})-\hat F=h_{\infty}=0$, and then
$F(\tilde{\mu})-\hat F=h_{\infty}=0$, and then ![]() $F(\tilde\mu)=\hat F$. Hencem
$F(\tilde\mu)=\hat F$. Hencem ![]() $\tilde{\mu}=\hat{\mu}$ by the uniqueness of the barycenter. This implies that
$\tilde{\mu}=\hat{\mu}$ by the uniqueness of the barycenter. This implies that ![]() $\mu_t\to\hat{\mu}$ in
$\mu_t\to\hat{\mu}$ in ![]() $\mathcal{W}_2(\mathcal{X})$ a.s. as
$\mathcal{W}_2(\mathcal{X})$ a.s. as ![]() $t\to \infty$.
$t\to \infty$.
Remark 1. Observe that, for a fixed ![]() $\mu\in\mathcal{W}_{2,\mathrm{ac}}(\mathcal{X})$ and a random
$\mu\in\mathcal{W}_{2,\mathrm{ac}}(\mathcal{X})$ and a random ![]() $m\sim\Pi$, the random variable
$m\sim\Pi$, the random variable ![]() $-(T_{\mu}^{m}-I)(x)$ is an unbiased estimator of
$-(T_{\mu}^{m}-I)(x)$ is an unbiased estimator of ![]() $F^\prime(\mu)(x)$ for
$F^\prime(\mu)(x)$ for ![]() $\mu({\mathrm{d}} x)$ almost eveywhere,
$\mu({\mathrm{d}} x)$ almost eveywhere, ![]() $x\in\mathbb{R}^q$. A natural way to jointly quantify the pointwise variances of these estimators is through the integrated variance,
$x\in\mathbb{R}^q$. A natural way to jointly quantify the pointwise variances of these estimators is through the integrated variance,
which is the equivalent (for unbiased estimators) of the mean integrated square error from non-parametric statistics [Reference Wasserman52]. Simple computations yield the following expresion for it, which will be useful in the next two sections:
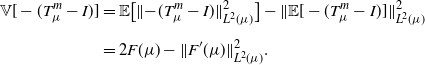 \begin{align} \mathbb{V}[-(T_{\mu}^{m}-I)] & = \mathbb{E}\big[\|{-}(T_{\mu}^{m}-I)\|_{L^2(\mu)}^2\big] - \|\mathbb{E}[-(T_{\mu}^{m}-I)]\|_{L^2(\mu)}^2 \notag \\[5pt] & = 2F(\mu) - \|F^\prime(\mu)\|_{L^2(\mu)}^2. \end{align}
\begin{align} \mathbb{V}[-(T_{\mu}^{m}-I)] & = \mathbb{E}\big[\|{-}(T_{\mu}^{m}-I)\|_{L^2(\mu)}^2\big] - \|\mathbb{E}[-(T_{\mu}^{m}-I)]\|_{L^2(\mu)}^2 \notag \\[5pt] & = 2F(\mu) - \|F^\prime(\mu)\|_{L^2(\mu)}^2. \end{align}
We close this section with the promised statement of Lemma 3, referred to in the introduction, giving us a sufficient condition for Assumption 2.
Lemma 3. If the support of ![]() $\Pi$ is
$\Pi$ is ![]() $\mathcal W_2(\mathbb R^d)$-compact and there is a constant
$\mathcal W_2(\mathbb R^d)$-compact and there is a constant ![]() $C_1<\infty$ such that
$C_1<\infty$ such that ![]() $\Pi(\{m\in\mathcal W_{2,\mathrm{ac}}(\mathbb R^d)\colon\int\log({\mathrm{d}} m/{\mathrm{d}} x)\,m({\mathrm{d}} x) \leq C_1\})=1$, then Assumption 2 is fulfilled.
$\Pi(\{m\in\mathcal W_{2,\mathrm{ac}}(\mathbb R^d)\colon\int\log({\mathrm{d}} m/{\mathrm{d}} x)\,m({\mathrm{d}} x) \leq C_1\})=1$, then Assumption 2 is fulfilled.
Proof. Let K be the support of ![]() $\Pi$, which is
$\Pi$, which is ![]() $\mathcal W_2(\mathbb R^d)$-compact. By the de la Vallée Poussin criterion, there is a
$\mathcal W_2(\mathbb R^d)$-compact. By the de la Vallée Poussin criterion, there is a ![]() $V\colon\mathbb R_+\to\mathbb R_+$, increasing, convex, and super-quadratic (i.e.
$V\colon\mathbb R_+\to\mathbb R_+$, increasing, convex, and super-quadratic (i.e. ![]() $\lim_{r\to +\infty} V(r)/r^2=+\infty$), such that
$\lim_{r\to +\infty} V(r)/r^2=+\infty$), such that ![]() $C_2\;:\!=\;\sup_{m\in K}\int V(\|x\|)\,m({\mathrm{d}} x)<\infty$. Observe that
$C_2\;:\!=\;\sup_{m\in K}\int V(\|x\|)\,m({\mathrm{d}} x)<\infty$. Observe that ![]() $p({\mathrm{d}} x)\;:\!=\;\exp\{-V(\|x\|)\}\,{\mathrm{d}} x$ is a finite measure (without loss of generality a probability measure). Moreover, for the relative entropy with respect to p we have
$p({\mathrm{d}} x)\;:\!=\;\exp\{-V(\|x\|)\}\,{\mathrm{d}} x$ is a finite measure (without loss of generality a probability measure). Moreover, for the relative entropy with respect to p we have ![]() $H(m\mid p)\;:\!=\;\int\log({\mathrm{d}} m/{\mathrm{d}} p)\,{\mathrm{d}} m=\int\log({\mathrm{d}} m/{\mathrm{d}} x)\,m({\mathrm{d}} x)+\int V(\|x\|)\,m({\mathrm{d}} x)$ if
$H(m\mid p)\;:\!=\;\int\log({\mathrm{d}} m/{\mathrm{d}} p)\,{\mathrm{d}} m=\int\log({\mathrm{d}} m/{\mathrm{d}} x)\,m({\mathrm{d}} x)+\int V(\|x\|)\,m({\mathrm{d}} x)$ if ![]() $m\ll {\mathrm{d}} x$ and
$m\ll {\mathrm{d}} x$ and ![]() $+\infty$ otherwise. Now define
$+\infty$ otherwise. Now define ![]() $K_\Pi\;:\!=\;\{m\in\mathcal W_{2,\mathrm{ac}}(\mathbb R^d)\colon H(m\mid p)\leq C_1+C_2,\, \int V(\|x\|)\,m({\mathrm{d}} x) \leq C_2\}$ so that
$K_\Pi\;:\!=\;\{m\in\mathcal W_{2,\mathrm{ac}}(\mathbb R^d)\colon H(m\mid p)\leq C_1+C_2,\, \int V(\|x\|)\,m({\mathrm{d}} x) \leq C_2\}$ so that ![]() $\Pi(K_\Pi)=1$. Clearly,
$\Pi(K_\Pi)=1$. Clearly, ![]() $K_\Pi$ is
$K_\Pi$ is ![]() $\mathcal W_2$-closed, since the relative entropy is weakly lower-semicontinuous, and also
$\mathcal W_2$-closed, since the relative entropy is weakly lower-semicontinuous, and also ![]() $\mathcal W_2$-relatively compact, since V is super-quadratic. Finally,
$\mathcal W_2$-relatively compact, since V is super-quadratic. Finally, ![]() $K_\Pi$ is geodesically convex by [Reference Villani50, Theorem 5.15].
$K_\Pi$ is geodesically convex by [Reference Villani50, Theorem 5.15].
For instance, if all m in the support of ![]() $\Pi$ is of the form
$\Pi$ is of the form
with ![]() $V_m$ bounded from below, then one way to guarantee the conditions in Lemma 3, assuming without loss of generality that
$V_m$ bounded from below, then one way to guarantee the conditions in Lemma 3, assuming without loss of generality that ![]() $V_m\geq 0$, is to ask that
$V_m\geq 0$, is to ask that ![]() $\int_y{\mathrm{e}}^{-V_m}(y)\,{\mathrm{d}} y \geq A$ and
$\int_y{\mathrm{e}}^{-V_m}(y)\,{\mathrm{d}} y \geq A$ and ![]() $\int_y|y|^{2+\varepsilon}{\mathrm{e}}^{-V_m}(y)\,{\mathrm{d}} y \leq B$ for some fixed
$\int_y|y|^{2+\varepsilon}{\mathrm{e}}^{-V_m}(y)\,{\mathrm{d}} y \leq B$ for some fixed ![]() $\varepsilon,A,B >0$. In words: tails are controlled and the measures cannot be too concentrated.
$\varepsilon,A,B >0$. In words: tails are controlled and the measures cannot be too concentrated.
4. A condition granting uniqueness of Karcher means and convergence rates
The aim of this section is to prove Theorem 2, a refinement of Theorem 1 under the additional assumption that the barycenter is a pseudo-associative Karcher mean. Notice that, with the notation introduced in Section 3, Definition 4 of pseudo-associative Karcher mean ![]() $\mu$ simply reads as
$\mu$ simply reads as
for all ![]() $\nu\in\mathcal W_{2,\mathrm{ac}}(\mathcal{X})$.
$\nu\in\mathcal W_{2,\mathrm{ac}}(\mathcal{X})$.
Remark 2. Suppose ![]() $\mu$ is a Karcher mean of
$\mu$ is a Karcher mean of ![]() $\Pi$ such that, for all
$\Pi$ such that, for all ![]() $\nu\in\mathcal W_{2,\mathrm{ac}}(\mathcal{X})$ and
$\nu\in\mathcal W_{2,\mathrm{ac}}(\mathcal{X})$ and ![]() $\Pi({\mathrm{d}} m)$ for almost every m,
$\Pi({\mathrm{d}} m)$ for almost every m,
Then, ![]() $\mu$ is pseudo-associative, with
$\mu$ is pseudo-associative, with ![]() $C_{\mu}=1$ and equality holding in Definition 4. Indeed, in that case we have
$C_{\mu}=1$ and equality holding in Definition 4. Indeed, in that case we have
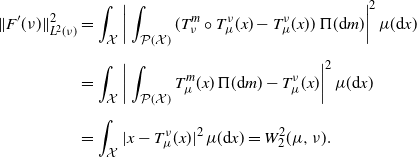 \begin{align*} \|F^\prime(\nu)\|^2_{L^2(\nu)} & = \int_{\mathcal{X}}\bigg|\int_{\mathcal P(\mathcal X)}(T_{\nu}^m \circ T_{\mu}^{\nu}(x)-T_{\mu}^{\nu}(x))\, \Pi({\mathrm{d}} m)\bigg|^2\,\mu({\mathrm{d}} x) \\[5pt] & = \int_{\mathcal{X}}\bigg|\int_{\mathcal P(\mathcal X)} T_{\mu}^{m}(x)\,\Pi({\mathrm{d}} m) - T_{\mu}^{\nu}(x)\bigg|^2\,\mu({\mathrm{d}} x) \\[5pt] & = \int_{\mathcal{X}}|x-T_{\mu}^{\nu}(x)|^2\,\mu({\mathrm{d}} x) = W_2^2(\mu,\nu). \end{align*}
\begin{align*} \|F^\prime(\nu)\|^2_{L^2(\nu)} & = \int_{\mathcal{X}}\bigg|\int_{\mathcal P(\mathcal X)}(T_{\nu}^m \circ T_{\mu}^{\nu}(x)-T_{\mu}^{\nu}(x))\, \Pi({\mathrm{d}} m)\bigg|^2\,\mu({\mathrm{d}} x) \\[5pt] & = \int_{\mathcal{X}}\bigg|\int_{\mathcal P(\mathcal X)} T_{\mu}^{m}(x)\,\Pi({\mathrm{d}} m) - T_{\mu}^{\nu}(x)\bigg|^2\,\mu({\mathrm{d}} x) \\[5pt] & = \int_{\mathcal{X}}|x-T_{\mu}^{\nu}(x)|^2\,\mu({\mathrm{d}} x) = W_2^2(\mu,\nu). \end{align*}
We will thus say that the Karcher mean ![]() $\mu$ is associative simply if (19) holds.
$\mu$ is associative simply if (19) holds.
The following is an analogue in Wasserstein space of a classical property implying convergence rates in gradient-type optimization algorithms.
Definition 5. We say that ![]() $\mu\in\mathcal W_{2,\mathrm{ac}}(\mathcal{X})$ satisfies a Polyak–Lojasiewicz inequality if
$\mu\in\mathcal W_{2,\mathrm{ac}}(\mathcal{X})$ satisfies a Polyak–Lojasiewicz inequality if
for some ![]() $\bar{C}_{\mu}>0$ and every
$\bar{C}_{\mu}>0$ and every ![]() $\nu\in\mathcal W_{2,\mathrm{ac}}(\mathcal{X})$.
$\nu\in\mathcal W_{2,\mathrm{ac}}(\mathcal{X})$.
We next state some useful properties.
Lemma 4. Suppose ![]() $\mu$ is a Karcher mean of
$\mu$ is a Karcher mean of ![]() $\Pi$. Then:
$\Pi$. Then:
(i) For all
 $\nu\in\mathcal W_{2,\mathrm{ac}}(\mathcal{X})$,
$\nu\in\mathcal W_{2,\mathrm{ac}}(\mathcal{X})$,  $F(\nu) -F(\mu) \leq \frac{1}{2}W_2^2(\mu,\nu)$.
$F(\nu) -F(\mu) \leq \frac{1}{2}W_2^2(\mu,\nu)$.-
(ii) If
 $\mu$ is pseudo-associative, then it is the unique barycenter, and it satisfies the Polyak–Lojasiewicz inequality (20) with
$\mu$ is pseudo-associative, then it is the unique barycenter, and it satisfies the Polyak–Lojasiewicz inequality (20) with  $\bar{C}_{\mu}=C_{\mu}$.
$\bar{C}_{\mu}=C_{\mu}$. -
(iii) If the associativity relation in (19) holds,
 $F(\nu) - F(\mu) = \frac{1}{2}W_2^2(\mu,\nu) = \frac{1}{2}\|F^\prime(\nu)\|^2_{L^2(\nu)}$.
$F(\nu) - F(\mu) = \frac{1}{2}W_2^2(\mu,\nu) = \frac{1}{2}\|F^\prime(\nu)\|^2_{L^2(\nu)}$.
Proof. For (i), we notice that this is a particular case of [Reference Chewi, Maunu, Rigollet and Stromme19, Theorem 7], which we can prove by an elementary argument based on the notion of Karcher mean. Indeed, by the definition of the function F and the fact that ![]() $(T_{\mu}^{\nu},T_{\mu}^m)(\mu)$ is a coupling of
$(T_{\mu}^{\nu},T_{\mu}^m)(\mu)$ is a coupling of ![]() $\nu$ and m,
$\nu$ and m,
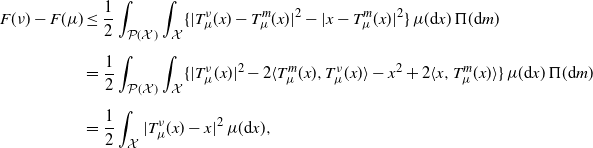 \begin{align*} F(\nu) - F(\mu) & \leq \frac{1}{2}\int_{\mathcal{P}(\mathcal{X})}\int_{\mathcal{X}}\{|T_{\mu}^{\nu}(x)-T_{\mu}^m(x)|^2-|x-T_{\mu}^m(x)|^2\}\, \mu({\mathrm{d}} x)\,\Pi({\mathrm{d}} m) \\[5pt] & = \frac{1}{2}\int_{\mathcal{P}(\mathcal{X})}\int_{\mathcal{X}}\{|T_{\mu}^{\nu}(x)|^2 - 2\langle T_{\mu}^m(x),T_{\mu}^{\nu}(x)\rangle - x^2 + 2\langle x,T_{\mu}^m(x)\rangle\}\,\mu({\mathrm{d}} x)\,\Pi({\mathrm{d}} m) \\[5pt] & = \frac{1}{2}\int_{\mathcal{X}}|T_{\mu}^{\nu}(x) - x|^2\,\mu({\mathrm{d}} x), \end{align*}
\begin{align*} F(\nu) - F(\mu) & \leq \frac{1}{2}\int_{\mathcal{P}(\mathcal{X})}\int_{\mathcal{X}}\{|T_{\mu}^{\nu}(x)-T_{\mu}^m(x)|^2-|x-T_{\mu}^m(x)|^2\}\, \mu({\mathrm{d}} x)\,\Pi({\mathrm{d}} m) \\[5pt] & = \frac{1}{2}\int_{\mathcal{P}(\mathcal{X})}\int_{\mathcal{X}}\{|T_{\mu}^{\nu}(x)|^2 - 2\langle T_{\mu}^m(x),T_{\mu}^{\nu}(x)\rangle - x^2 + 2\langle x,T_{\mu}^m(x)\rangle\}\,\mu({\mathrm{d}} x)\,\Pi({\mathrm{d}} m) \\[5pt] & = \frac{1}{2}\int_{\mathcal{X}}|T_{\mu}^{\nu}(x) - x|^2\,\mu({\mathrm{d}} x), \end{align*}
where in the second equality we twice used the fact that ![]() $\int_{\mathcal{P)}(\mathcal{X}) } T_{\mu}^{m}(x) \Pi(dm) = x$ for
$\int_{\mathcal{P)}(\mathcal{X}) } T_{\mu}^{m}(x) \Pi(dm) = x$ for ![]() $\mu({\mathrm{d}} x)$ a.e. x.
$\mu({\mathrm{d}} x)$ a.e. x.
For (ii), the claim is obvious in view of the previous argument and (18).
For (iii), taking into account Remark 2, it is enough to notice that
under (19), in which case the inequality in the proof of (i) is an equality.
Remark 3. Recall that ![]() $\Pi$ is said to satisfy a variance inequality [Reference Ahidar-Coutrix, Le Gouic and Paris2] if, for some constant
$\Pi$ is said to satisfy a variance inequality [Reference Ahidar-Coutrix, Le Gouic and Paris2] if, for some constant ![]() $C>0$,
$C>0$, ![]() $F(\nu) - F(\hat\mu) \geq \frac{1}{2}CW_2^2(\hat\mu,\nu)$, with
$F(\nu) - F(\hat\mu) \geq \frac{1}{2}CW_2^2(\hat\mu,\nu)$, with ![]() $\hat{\mu}$ the barycenter of
$\hat{\mu}$ the barycenter of ![]() $\Pi$. It readily follows that
$\Pi$. It readily follows that ![]() $\hat\mu$ is a pseudo-associative Karcher mean as soon as a variance inequality and the Polyak–Lojasiewicz inequality 20 hold. That was the case in [Reference Chewi, Maunu, Rigollet and Stromme19], and so the barycenter in the Gaussian setting considered therein is a pseudo-associative Karcher mean too. Notice that if the barycenter is associative, by Lemma 4(iii) the variance inequality holds; this is the case for the examples discussed in Sections 6.1–6.3. Notice also that, if a variance inequality holds, bounds on the optimality gap for the SDG sequence as in Theorem 2 immediately yield similar bounds for the expected squared Wasserstein distance
$\hat\mu$ is a pseudo-associative Karcher mean as soon as a variance inequality and the Polyak–Lojasiewicz inequality 20 hold. That was the case in [Reference Chewi, Maunu, Rigollet and Stromme19], and so the barycenter in the Gaussian setting considered therein is a pseudo-associative Karcher mean too. Notice that if the barycenter is associative, by Lemma 4(iii) the variance inequality holds; this is the case for the examples discussed in Sections 6.1–6.3. Notice also that, if a variance inequality holds, bounds on the optimality gap for the SDG sequence as in Theorem 2 immediately yield similar bounds for the expected squared Wasserstein distance ![]() $\mathbb{E}[W_2^2(\mu_k,\hat{\mu})]$.
$\mathbb{E}[W_2^2(\mu_k,\hat{\mu})]$.
Proof of Theorem 2. If we assume the pseudo-associtativity condition (5) holds, the uniqueness of Karcher means (hence equal to the barycenter) is immediate, as noted in Section 1. Under that assumption, the inequality (20) holds thanks to Lemma 4(ii), and convergence estimates can then be deduced by adapting classic arguments of the SGD algorithm in an Euclidean setting; see, e.g., [Reference Bottou, Curtis and Nocedal15]. Indeed, by Proposition 2, (17), and (20),
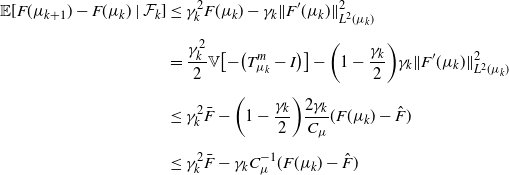 \begin{align*} \mathbb{E}[F(\mu_{k+1}) - F(\mu_k)\mid\mathcal F_{k}] & \leq \gamma_k^2F(\mu_k) - \gamma_k\|F^\prime(\mu_k)\|^2_{L^2(\mu_k)} \\[5pt] & = \frac{\gamma_k^2}{2}\mathbb{V}\big[{-}\big(T_{\mu_k}^{m}-I\big)\big] - \bigg(1 - \frac{\gamma_k}{2}\bigg)\gamma_k\|F^\prime(\mu_k)\|^2_{L^2(\mu_k)} \\[5pt] & \leq \gamma_k^2\bar{F} - \bigg(1 - \frac{\gamma_k}{2}\bigg)\frac{2\gamma_k}{C_{\mu}}(F(\mu_k) - \hat{F}) \\[5pt] & \leq \gamma_k^2\bar{F} - \gamma_k C_{\mu}^{-1}(F(\mu_k) - \hat{F}) \end{align*}
\begin{align*} \mathbb{E}[F(\mu_{k+1}) - F(\mu_k)\mid\mathcal F_{k}] & \leq \gamma_k^2F(\mu_k) - \gamma_k\|F^\prime(\mu_k)\|^2_{L^2(\mu_k)} \\[5pt] & = \frac{\gamma_k^2}{2}\mathbb{V}\big[{-}\big(T_{\mu_k}^{m}-I\big)\big] - \bigg(1 - \frac{\gamma_k}{2}\bigg)\gamma_k\|F^\prime(\mu_k)\|^2_{L^2(\mu_k)} \\[5pt] & \leq \gamma_k^2\bar{F} - \bigg(1 - \frac{\gamma_k}{2}\bigg)\frac{2\gamma_k}{C_{\mu}}(F(\mu_k) - \hat{F}) \\[5pt] & \leq \gamma_k^2\bar{F} - \gamma_k C_{\mu}^{-1}(F(\mu_k) - \hat{F}) \end{align*}
for some finite (deterministic) upper bound ![]() $\bar{F}>0$ of the sequence
$\bar{F}>0$ of the sequence ![]() $(F(\mu_t))_{t\geq 1}$ under Assumption 2′. In the last line we used the fact that
$(F(\mu_t))_{t\geq 1}$ under Assumption 2′. In the last line we used the fact that ![]() $\gamma_k\leq\gamma_0\leq1$ for the choice
$\gamma_k\leq\gamma_0\leq1$ for the choice ![]() $\gamma_k={a}/({b+k})$ with fixed
$\gamma_k={a}/({b+k})$ with fixed ![]() $b\geq a>0$. It follows that
$b\geq a>0$. It follows that
Assume now that ![]() $ a>C_{\hat \mu}$ and that, for certain
$ a>C_{\hat \mu}$ and that, for certain ![]() $c\geq a^2 \bar{F}/(C_{\hat \mu}^{-1}a-1)>0$ and a given
$c\geq a^2 \bar{F}/(C_{\hat \mu}^{-1}a-1)>0$ and a given ![]() $k\in\mathbb{N}$,
$k\in\mathbb{N}$,
Let us show that ![]() $\mathbb{E}[F(\mu_{k+1}) - \hat{F}]\leq c/(b+k+1)$ too. By (21),
$\mathbb{E}[F(\mu_{k+1}) - \hat{F}]\leq c/(b+k+1)$ too. By (21),
where we used the choice of c in the second inequality. Taking
the inequality in (22) holds for ![]() $k=0$, and hence for all
$k=0$, and hence for all ![]() $k\in \mathbb{N}$ by induction.
$k\in \mathbb{N}$ by induction.
Concerning the a.s. weak convergence of ![]() $\mu_k$ to
$\mu_k$ to ![]() $\hat\mu$, we can follow the proof of Theorem 1 up to (15), and then derive in the present setting (16), i.e.
$\hat\mu$, we can follow the proof of Theorem 1 up to (15), and then derive in the present setting (16), i.e.
from the Polyak–Lojasiewicz inequality (20), which holds thanks to Lemma 4(ii). As before, this is then used to obtain that ![]() $F(\mu_k)\to\hat F$ almost surely. Since
$F(\mu_k)\to\hat F$ almost surely. Since ![]() $K_\Pi$ is
$K_\Pi$ is ![]() $\mathcal W_2$-bounded, it is in particular tight. The fact that
$\mathcal W_2$-bounded, it is in particular tight. The fact that ![]() $\nu\mapsto F(\nu)$ is weakly lower semicontinuous and the uniqueness of minimizers of F now entail that, almost surely,
$\nu\mapsto F(\nu)$ is weakly lower semicontinuous and the uniqueness of minimizers of F now entail that, almost surely, ![]() $\mu_k\to\hat\mu$ weakly.
$\mu_k\to\hat\mu$ weakly.
Remark 4. In addition to concluding that, almost surely, ![]() $\mu_k\to\hat\mu$ weakly, the above proof also establishes the a.s. existence of a subsequence
$\mu_k\to\hat\mu$ weakly, the above proof also establishes the a.s. existence of a subsequence ![]() $n_k$ such that
$n_k$ such that ![]() $\mu_{n_k}\to\hat\mu$ in
$\mu_{n_k}\to\hat\mu$ in ![]() $\mathcal W_2$. Indeed, this follows from (15) together with (18).
$\mathcal W_2$. Indeed, this follows from (15) together with (18).
The above proof shows that we may relax the definition of pseudo-associativity by requiring (5) to hold for ![]() $\nu\in K_\Pi$ (or more precisely, for
$\nu\in K_\Pi$ (or more precisely, for ![]() $\nu\in\{\mu_k\colon k\in\mathbb N\}$) only.
$\nu\in\{\mu_k\colon k\in\mathbb N\}$) only.
5. Variance reduction via batch SGD
Paralleling the Euclidean setting, the function ![]() $-\big(T_{\mu_k}^{m_k}-I\big)$ can be seen as an estimator of the gradient in the kth step of the SGD scheme. Hence, conditionally on
$-\big(T_{\mu_k}^{m_k}-I\big)$ can be seen as an estimator of the gradient in the kth step of the SGD scheme. Hence, conditionally on ![]() $m_0,\dots,m_{k-1}$, its integrated variance given by
$m_0,\dots,m_{k-1}$, its integrated variance given by ![]() $2F(\mu_k)-\|F^\prime(\mu_k)\|_{L^2(\mu_k)}^2$ could be large for some sampled
$2F(\mu_k)-\|F^\prime(\mu_k)\|_{L^2(\mu_k)}^2$ could be large for some sampled ![]() $\mu_k$, which would yield a slow convergence if the steps
$\mu_k$, which would yield a slow convergence if the steps ![]() $\gamma_k$ are not small enough. To cope with this issue, as customary in stochastic algorithms, we are led to consider alternative estimators of
$\gamma_k$ are not small enough. To cope with this issue, as customary in stochastic algorithms, we are led to consider alternative estimators of ![]() $F^\prime(\mu)$ with less (integrated) variance.
$F^\prime(\mu)$ with less (integrated) variance.
Definition 6. Let ![]() $\mu_0 \in K_\Pi$,
$\mu_0 \in K_\Pi$, ![]() $m_k^i\stackrel{\mathrm{i.i.d.}}{\sim}\Pi$, and
$m_k^i\stackrel{\mathrm{i.i.d.}}{\sim}\Pi$, and ![]() $\gamma_k > 0$ for
$\gamma_k > 0$ for ![]() $k \geq 0$ and
$k \geq 0$ and ![]() $i=1,\dots,S_k$. The batch stochastic gradient descent (BSGD) sequence is given by
$i=1,\dots,S_k$. The batch stochastic gradient descent (BSGD) sequence is given by
 \begin{equation} \mu_{k+1} \;:\!=\; \Bigg[(1-\gamma_k)I + \gamma_k\frac{1}{S_k}\sum_{i=1}^{S_k}T_{\mu_k}^{m_k^i}\Bigg](\mu_k). \end{equation}
\begin{equation} \mu_{k+1} \;:\!=\; \Bigg[(1-\gamma_k)I + \gamma_k\frac{1}{S_k}\sum_{i=1}^{S_k}T_{\mu_k}^{m_k^i}\Bigg](\mu_k). \end{equation}
Notice that ![]() $({1}/{S_k})\sum_{i=1}^{S_k}T_{\mu_k}^{m_k^i} - I$ is an unbiased estimator of
$({1}/{S_k})\sum_{i=1}^{S_k}T_{\mu_k}^{m_k^i} - I$ is an unbiased estimator of ![]() $-F^\prime(\mu_k)$. Proceeding as in Proposition 2, with
$-F^\prime(\mu_k)$. Proceeding as in Proposition 2, with ![]() $\mathcal F_{k+1}$ now denoting the sigma-algebra generated by
$\mathcal F_{k+1}$ now denoting the sigma-algebra generated by ![]() $\{m_\ell^i\colon\ell\leq k,\,i\leq S_k\}$, and writing
$\{m_\ell^i\colon\ell\leq k,\,i\leq S_k\}$, and writing ![]() $\Pi$ also for the law of an i.i.d. sample of size
$\Pi$ also for the law of an i.i.d. sample of size ![]() $S_k$, we now have
$S_k$, we now have
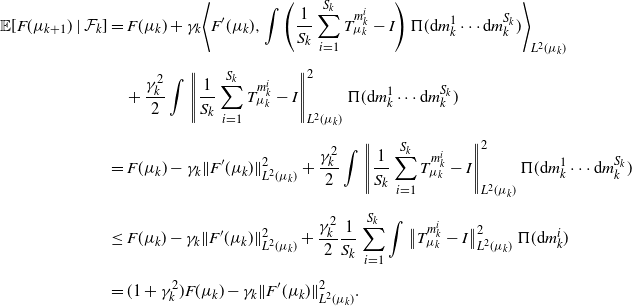 \begin{align*} \mathbb{E}[F(\mu_{k+1})\mid\mathcal F_k] & = F(\mu_k) + \gamma_k\Bigg\langle F^\prime(\mu_k),\int\Bigg(\frac{1}{S_k}\sum_{i=1}^{S_k}T_{\mu_k}^{m_k^i}-I\Bigg)\, \Pi({\mathrm{d}} m_k^1\cdots{\mathrm{d}} m_k^{S_k})\Bigg\rangle_{L^2(\mu_k)} \\[5pt] & \quad + \frac{\gamma_k^2}{2}\int\Bigg\|\frac{1}{S_k}\sum_{i=1}^{S_k}T_{\mu_k}^{m_k^i}-I\Bigg\|^2_{L^2(\mu_k)}\, \Pi({\mathrm{d}} m_k^1\cdots{\mathrm{d}} m_k^{S_k}) \\[5pt] & = F(\mu_k) - \gamma_k\|F^\prime(\mu_k)\|^2_{L^2(\mu_k)} + \frac{\gamma_k^2}{2}\int\Bigg\|\frac{1}{S_k}\sum_{i=1}^{S_k}T_{\mu_k}^{m_k^i}-I\Bigg\|^2_{L^2(\mu_k)}\, \Pi({\mathrm{d}} m_k^1\cdots{\mathrm{d}} m_k^{S_k}) \\[5pt] & \leq F(\mu_k) - \gamma_k\|F^\prime(\mu_k)\|^2_{L^2(\mu_k)} + \frac{\gamma_k^2}{2}\frac{1}{S_k}\sum_{i=1}^{S_k}\int\big\|T_{\mu_k}^{m_k^i}-I\big\|^2_{L^2(\mu_k)}\,\Pi({\mathrm{d}} m_k^i) \\[5pt] & = (1+\gamma_k^2)F(\mu_k) - \gamma_k\|F^\prime(\mu_k)\|^2_{L^2(\mu_k)}.\end{align*}
\begin{align*} \mathbb{E}[F(\mu_{k+1})\mid\mathcal F_k] & = F(\mu_k) + \gamma_k\Bigg\langle F^\prime(\mu_k),\int\Bigg(\frac{1}{S_k}\sum_{i=1}^{S_k}T_{\mu_k}^{m_k^i}-I\Bigg)\, \Pi({\mathrm{d}} m_k^1\cdots{\mathrm{d}} m_k^{S_k})\Bigg\rangle_{L^2(\mu_k)} \\[5pt] & \quad + \frac{\gamma_k^2}{2}\int\Bigg\|\frac{1}{S_k}\sum_{i=1}^{S_k}T_{\mu_k}^{m_k^i}-I\Bigg\|^2_{L^2(\mu_k)}\, \Pi({\mathrm{d}} m_k^1\cdots{\mathrm{d}} m_k^{S_k}) \\[5pt] & = F(\mu_k) - \gamma_k\|F^\prime(\mu_k)\|^2_{L^2(\mu_k)} + \frac{\gamma_k^2}{2}\int\Bigg\|\frac{1}{S_k}\sum_{i=1}^{S_k}T_{\mu_k}^{m_k^i}-I\Bigg\|^2_{L^2(\mu_k)}\, \Pi({\mathrm{d}} m_k^1\cdots{\mathrm{d}} m_k^{S_k}) \\[5pt] & \leq F(\mu_k) - \gamma_k\|F^\prime(\mu_k)\|^2_{L^2(\mu_k)} + \frac{\gamma_k^2}{2}\frac{1}{S_k}\sum_{i=1}^{S_k}\int\big\|T_{\mu_k}^{m_k^i}-I\big\|^2_{L^2(\mu_k)}\,\Pi({\mathrm{d}} m_k^i) \\[5pt] & = (1+\gamma_k^2)F(\mu_k) - \gamma_k\|F^\prime(\mu_k)\|^2_{L^2(\mu_k)}.\end{align*}
The arguments in the proof of Theorem 1 can then be easily adapted to get the following result.
Theorem 3. Under the assumptions of Theorem 1, the BSGD sequence ![]() $\{\mu_t\}_{t\geq0}$ in (23) converges almost surely to the 2-Wasserstein barycenter of
$\{\mu_t\}_{t\geq0}$ in (23) converges almost surely to the 2-Wasserstein barycenter of ![]() $\Pi$.
$\Pi$.
The supporting idea for using mini-batches is reducing the noise of the estimator of ![]() $F^\prime(\mu)$.
$F^\prime(\mu)$.
Proposition 3. The integrated variance of the mini-batch estimator of fixed batch size S for ![]() $F^\prime(\mu)$, given by
$F^\prime(\mu)$, given by ![]() $-({1}/{S})\sum_{i=1}^{S}\big(T_{\mu}^{m_i}-I\big)$, decreases linearly in the sample size. More precisely,
$-({1}/{S})\sum_{i=1}^{S}\big(T_{\mu}^{m_i}-I\big)$, decreases linearly in the sample size. More precisely,
 $$ \mathbb{V}\Bigg[{-}\frac{1}{S}\sum_{i=1}^{S}\big(T_{\mu}^{m_i}-I\big)\Bigg] = \frac{1}{S}\mathbb{V}\big[{-}\big(T_{\mu}^{m_1}-I\big)\big] = \frac{1}{S}\big[2F(\mu) - \|F^\prime(\mu)\|_{L^2(\mu)}^2\big]. $$
$$ \mathbb{V}\Bigg[{-}\frac{1}{S}\sum_{i=1}^{S}\big(T_{\mu}^{m_i}-I\big)\Bigg] = \frac{1}{S}\mathbb{V}\big[{-}\big(T_{\mu}^{m_1}-I\big)\big] = \frac{1}{S}\big[2F(\mu) - \|F^\prime(\mu)\|_{L^2(\mu)}^2\big]. $$
Proof. In a similar way to (17), the integrated variance of the mini-batch estimator is
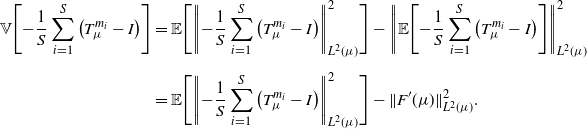 \begin{align*} \mathbb{V}\Bigg[{-}\frac{1}{S}\sum_{i=1}^{S}\big(T_{\mu}^{m_i}-I\big)\Bigg] & = \mathbb{E}\Bigg[\Bigg\|{-}\frac{1}{S}\sum_{i=1}^{S}\big(T_{\mu}^{m_i}-I\big)\Bigg\|_{L^2(\mu)}^2\Bigg] - \Bigg\|\mathbb{E}\Bigg[{-}\frac{1}{S}\sum_{i=1}^{S}\big(T_{\mu}^{m_i}-I\big)\Bigg]\Bigg\|_{L^2(\mu)}^2 \\[5pt] & = \mathbb{E}\Bigg[\Bigg\|{-}\frac{1}{S}\sum_{i=1}^{S}\big(T_{\mu}^{m_i}-I\big)\Bigg\|_{L^2(\mu)}^2\Bigg] - \|F^\prime(\mu)\|_{L^2(\mu)}^2. \end{align*}
\begin{align*} \mathbb{V}\Bigg[{-}\frac{1}{S}\sum_{i=1}^{S}\big(T_{\mu}^{m_i}-I\big)\Bigg] & = \mathbb{E}\Bigg[\Bigg\|{-}\frac{1}{S}\sum_{i=1}^{S}\big(T_{\mu}^{m_i}-I\big)\Bigg\|_{L^2(\mu)}^2\Bigg] - \Bigg\|\mathbb{E}\Bigg[{-}\frac{1}{S}\sum_{i=1}^{S}\big(T_{\mu}^{m_i}-I\big)\Bigg]\Bigg\|_{L^2(\mu)}^2 \\[5pt] & = \mathbb{E}\Bigg[\Bigg\|{-}\frac{1}{S}\sum_{i=1}^{S}\big(T_{\mu}^{m_i}-I\big)\Bigg\|_{L^2(\mu)}^2\Bigg] - \|F^\prime(\mu)\|_{L^2(\mu)}^2. \end{align*}
The first term can be expanded as
 \begin{align*} \Bigg\|{-}\frac{1}{S}\sum_{i=1}^{S}\big(T_{\mu}^{m_i}-I\big)\Bigg\|_{L^2(\mu)}^2 & = \frac{1}{S^2}\Bigg\langle\sum_{i=1}^{S}\big(T_{\mu}^{m_i}-I\big), \sum_{j=1}^{S}\big(T_{\mu}^{m_j}-I\big)\Bigg\rangle_{L^2(\mu)} \\[5pt] & = \frac{1}{S^2}\sum_{i=1}^{S}\sum_{j=1}^{S}\big\langle T_{\mu}^{m_i}-I,T_{\mu}^{m_j}-I\big\rangle_{L^2(\mu)} \\[5pt] & =\frac{1}{S^2}\sum_{i=1}^{S}\big\|{-}\big(T_{\mu}^{m_i}-I\big)\big\|_{L^2(\mu)}^2 + \frac{1}{S^2}\sum_{j \neq i}^{S}\big\langle T_{\mu}^{m_i}-I,T_{\mu}^{m_j}-I\big\rangle_{L^2(\mu)}. \end{align*}
\begin{align*} \Bigg\|{-}\frac{1}{S}\sum_{i=1}^{S}\big(T_{\mu}^{m_i}-I\big)\Bigg\|_{L^2(\mu)}^2 & = \frac{1}{S^2}\Bigg\langle\sum_{i=1}^{S}\big(T_{\mu}^{m_i}-I\big), \sum_{j=1}^{S}\big(T_{\mu}^{m_j}-I\big)\Bigg\rangle_{L^2(\mu)} \\[5pt] & = \frac{1}{S^2}\sum_{i=1}^{S}\sum_{j=1}^{S}\big\langle T_{\mu}^{m_i}-I,T_{\mu}^{m_j}-I\big\rangle_{L^2(\mu)} \\[5pt] & =\frac{1}{S^2}\sum_{i=1}^{S}\big\|{-}\big(T_{\mu}^{m_i}-I\big)\big\|_{L^2(\mu)}^2 + \frac{1}{S^2}\sum_{j \neq i}^{S}\big\langle T_{\mu}^{m_i}-I,T_{\mu}^{m_j}-I\big\rangle_{L^2(\mu)}. \end{align*}
By taking expectation, as the samples ![]() $m_i \sim \Pi$ are independent, we get
$m_i \sim \Pi$ are independent, we get
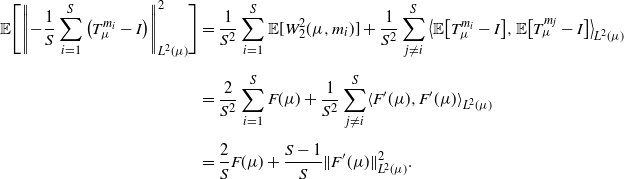 \begin{align*} \mathbb{E}\Bigg[\Bigg\|{-}\frac{1}{S}\sum_{i=1}^{S}\big(T_{\mu}^{m_i}-I\big)\Bigg\|_{L^2(\mu)}^2\Bigg] & = \frac{1}{S^2}\sum_{i=1}^{S}\mathbb{E}[W_2^2(\mu,m_i)] + \frac{1}{S^2}\sum_{j \neq i}^{S}\big\langle\mathbb{E}\big[T_{\mu}^{m_i}-I\big], \mathbb{E}\big[T_{\mu}^{m_j}-I\big]\big\rangle_{L^2(\mu)} \\[5pt] & = \frac{2}{S^2}\sum_{i=1}^{S}F(\mu) + \frac{1}{S^2}\sum_{j \neq i}^{S}\langle F^\prime(\mu),F^\prime(\mu)\rangle_{L^2(\mu)} \\[5pt] & = \frac{2}{S}F(\mu) + \frac{S-1}{S}\|F^\prime(\mu)\|_{L^2(\mu)}^2. \end{align*}
\begin{align*} \mathbb{E}\Bigg[\Bigg\|{-}\frac{1}{S}\sum_{i=1}^{S}\big(T_{\mu}^{m_i}-I\big)\Bigg\|_{L^2(\mu)}^2\Bigg] & = \frac{1}{S^2}\sum_{i=1}^{S}\mathbb{E}[W_2^2(\mu,m_i)] + \frac{1}{S^2}\sum_{j \neq i}^{S}\big\langle\mathbb{E}\big[T_{\mu}^{m_i}-I\big], \mathbb{E}\big[T_{\mu}^{m_j}-I\big]\big\rangle_{L^2(\mu)} \\[5pt] & = \frac{2}{S^2}\sum_{i=1}^{S}F(\mu) + \frac{1}{S^2}\sum_{j \neq i}^{S}\langle F^\prime(\mu),F^\prime(\mu)\rangle_{L^2(\mu)} \\[5pt] & = \frac{2}{S}F(\mu) + \frac{S-1}{S}\|F^\prime(\mu)\|_{L^2(\mu)}^2. \end{align*}
Subtracting ![]() $\|F^\prime(\mu)\|_{L^2(\mu)}^2$ yields the asserted identities.
$\|F^\prime(\mu)\|_{L^2(\mu)}^2$ yields the asserted identities.
The mini-batch implementation is easily seen to inherit the convergence estimates established in Theorem 2.
Theorem 4. Under the assumptions of Theorem 2, the BSGD sequence ![]() $\{\mu_k\}_k$ in (23) is almost surely convergent to
$\{\mu_k\}_k$ in (23) is almost surely convergent to ![]() $\hat{\mu}\in K_\Pi$ as soon as (3) and (4) hold. Moreover, for every
$\hat{\mu}\in K_\Pi$ as soon as (3) and (4) hold. Moreover, for every ![]() $a>C_{\hat{\mu}}^{-1}$ and
$a>C_{\hat{\mu}}^{-1}$ and ![]() $b\geq a$ there exists an explicit constant
$b\geq a$ there exists an explicit constant ![]() $C_{a,b}>0$ such that, if
$C_{a,b}>0$ such that, if ![]() $\gamma_k={a}/({b+k})$ for all
$\gamma_k={a}/({b+k})$ for all ![]() $k\in \mathbb{N}$, the expected optimallity gap satisfies
$k\in \mathbb{N}$, the expected optimallity gap satisfies
6. SGD for closed-form Wasserstein barycenters
As discussed in the introduction, recent developments have enabled the approximate computation of optimal transport maps between two given absolutely continuous distributions, and hence the practical implementation of the SGD in fairly general cases is feasible in principle. We will not address this issue in the present work, but rather content ourselves with analyzing some families of models considered in [Reference Álvarez-Esteban, del Barrio, Cuesta-Albertos and Matrán5, Reference Cuesta-Albertos, Ruschendorf and Tuero-Diaz24] for which this additional algorithmic aspect can be avoided, their optimal transport maps being explicit and easy to evaluate. Further, we will examine some of their closure properties that are preserved under the operation of taking barycenter. This is important, for instance, in the context of the statistical application in [Reference Backhoff-Veraguas, Fontbona, Rios and Tobar9], wherein ![]() $\Pi$ really represents a posterior distribution on models and its barycenter is postulated as a useful representative of the posterior distribution on models. It is thus desirable that the representative model share some of the properties of all the models charged by the posterior.
$\Pi$ really represents a posterior distribution on models and its barycenter is postulated as a useful representative of the posterior distribution on models. It is thus desirable that the representative model share some of the properties of all the models charged by the posterior.
In the settings that will be presented, the pseudo-associativity condition (5) is either satisfied or conditions ensuring it can be given explicitly. Convergence bounds as in Theorem 2 can be easily deduced in those cases for each specification of ![]() ${\Pi}$ satisfying the required assumptions.
${\Pi}$ satisfying the required assumptions.
6.1. Univariate distributions
We assume that m is a continuous distribution over ![]() $\mathbb{R}$, and denote respectively by
$\mathbb{R}$, and denote respectively by ![]() $F_m$ and
$F_m$ and ![]() $Q_m\;:\!=\;F_m^{-1}$ its cumulative distribution function and its right-continuous quantile function. The increasing transport map from a continuous
$Q_m\;:\!=\;F_m^{-1}$ its cumulative distribution function and its right-continuous quantile function. The increasing transport map from a continuous ![]() $m_0$ to m, also known as the monotone rearrangement, is given by
$m_0$ to m, also known as the monotone rearrangement, is given by ![]() $T_{m_0}^m(x) = Q_{m}(F_{m_0}(x))$, and is known to be p-Wasserstein optimal for
$T_{m_0}^m(x) = Q_{m}(F_{m_0}(x))$, and is known to be p-Wasserstein optimal for ![]() $p\geq1$ (see [Reference Villani50, Remark 2.19(iv)]). Given
$p\geq1$ (see [Reference Villani50, Remark 2.19(iv)]). Given ![]() $\Pi$, the barycenter
$\Pi$, the barycenter ![]() $\hat{m}$ is also independent of p and characterized via its quantile, i.e.
$\hat{m}$ is also independent of p and characterized via its quantile, i.e.
In words: the quantile function of the barycenter is equal to the average quantile function. Our SGD iteration, starting from a distribution function ![]() $F_{\mu}(x)$, sampling some
$F_{\mu}(x)$, sampling some ![]() $m \sim \Pi$, and with step
$m \sim \Pi$, and with step ![]() $\gamma$, produces the measure
$\gamma$, produces the measure ![]() $\nu = ((1-\gamma)I + \gamma T_\mu^m)(\mu)$. This is characterized by its quantile function,
$\nu = ((1-\gamma)I + \gamma T_\mu^m)(\mu)$. This is characterized by its quantile function, ![]() $Q_{\nu}(\!\cdot\!) = (1-\gamma)Q_{\mu}(\!\cdot\!) + \gamma Q_m(\!\cdot\!)$. The BSGD iteration is
$Q_{\nu}(\!\cdot\!) = (1-\gamma)Q_{\mu}(\!\cdot\!) + \gamma Q_m(\!\cdot\!)$. The BSGD iteration is
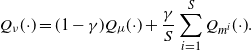 $$Q_{\nu}(\!\cdot\!) = (1-\gamma)Q_{\mu}(\!\cdot\!) + \frac{\gamma}{S} \sum_{i=1}^{S} Q_{m^{i}}(\!\cdot\!).$$
$$Q_{\nu}(\!\cdot\!) = (1-\gamma)Q_{\mu}(\!\cdot\!) + \frac{\gamma}{S} \sum_{i=1}^{S} Q_{m^{i}}(\!\cdot\!).$$
As explained in Remark 2, the barycenter is automatically pseudo-associative, since transport maps (i.e. increasing functions) are in this case associative in the sense discussed therein, and hence Theorem 2 applies. Moreover, by Remark 3, it entails convergence bounds in ![]() $W_2^2$ for the SGD sequence itself.
$W_2^2$ for the SGD sequence itself.
Interestingly, the model average ![]() $\bar{m}\;:\!=\;\int m\,\Pi({\mathrm{d}} m)$ is characterized by the averaged cumulative distribution function, i.e.
$\bar{m}\;:\!=\;\int m\,\Pi({\mathrm{d}} m)$ is characterized by the averaged cumulative distribution function, i.e. ![]() $F_{\bar{m}}(\!\cdot\!) = \int F_m(\!\cdot\!)\,\Pi({\mathrm{d}} m)$. The model average does not preserve intrinsic shape properties from the distributions such as symmetry or unimodality. For example, if
$F_{\bar{m}}(\!\cdot\!) = \int F_m(\!\cdot\!)\,\Pi({\mathrm{d}} m)$. The model average does not preserve intrinsic shape properties from the distributions such as symmetry or unimodality. For example, if ![]() $\Pi = 0.3\times\delta_{m_1} + 0.7\times\delta_{m_2}$ with
$\Pi = 0.3\times\delta_{m_1} + 0.7\times\delta_{m_2}$ with ![]() $m_1 = \mathcal{N}(1,1)$ and
$m_1 = \mathcal{N}(1,1)$ and ![]() $m_2=\mathcal{N}(3,1)$, the model average is an asymmetric bimodal distribution with modes on 1 and 3, while the Wasserstein barycenter is the Gaussian distribution
$m_2=\mathcal{N}(3,1)$, the model average is an asymmetric bimodal distribution with modes on 1 and 3, while the Wasserstein barycenter is the Gaussian distribution ![]() $\hat m = \mathcal{N}(2.4,1)$.
$\hat m = \mathcal{N}(2.4,1)$.
The following reasoning illustrates the fact that Wasserstein barycenters preserve geometric properties in a way that, e.g., the model average does not. A continuous distribution m on ![]() $\mathbb{R}$ is unimodal with a mode on
$\mathbb{R}$ is unimodal with a mode on ![]() $\tilde{x}_m$ if its quantile function Q(y) is concave for
$\tilde{x}_m$ if its quantile function Q(y) is concave for ![]() $y < \tilde{y}_m$ and convex for
$y < \tilde{y}_m$ and convex for ![]() $y > \tilde{y}_m$, where
$y > \tilde{y}_m$, where ![]() $Q(\tilde{y}_m) = \tilde{x}_m$. Likewise, m is symmetric with respect to
$Q(\tilde{y}_m) = \tilde{x}_m$. Likewise, m is symmetric with respect to ![]() $x_m\in\mathbb{R}$ if
$x_m\in\mathbb{R}$ if ![]() $Q\big(\frac{1}{2}+y\big) = 2x_m - Q\big(\frac{1}{2}-y\big)$ for
$Q\big(\frac{1}{2}+y\big) = 2x_m - Q\big(\frac{1}{2}-y\big)$ for ![]() $y \in \big[0,\frac{1}{2}\big]$ note that
$y \in \big[0,\frac{1}{2}\big]$ note that ![]() $\big(x_m =Q_m\big(\frac{1}{2}\big)\big)$. These properties can be analogously described in terms of the function
$\big(x_m =Q_m\big(\frac{1}{2}\big)\big)$. These properties can be analogously described in terms of the function ![]() $F_m$. Let us show that the barycenter preserves unimodality/symmetry.
$F_m$. Let us show that the barycenter preserves unimodality/symmetry.
Proposition 4. If ![]() $\Pi$ is concentrated on continuous symmetric (resp. symmetric unimodal) univariate distributions, then the barycenter
$\Pi$ is concentrated on continuous symmetric (resp. symmetric unimodal) univariate distributions, then the barycenter ![]() $\hat{m}$ is symmetric (resp. symmetric unimodal).
$\hat{m}$ is symmetric (resp. symmetric unimodal).
Proof. Using the quantile function characterization in (24) we have, for ![]() $y\in\big[0,\frac{1}{2}\big]$,
$y\in\big[0,\frac{1}{2}\big]$,
where ![]() $x_{\hat{m}}\;:\!=\; \int x_m\,\Pi({\mathrm{d}} m)$. In other words,
$x_{\hat{m}}\;:\!=\; \int x_m\,\Pi({\mathrm{d}} m)$. In other words, ![]() $\hat{m}$ is symmetric with respect to
$\hat{m}$ is symmetric with respect to ![]() $x_{\hat{m}}$. Now, if each m is unimodal in addition to symmetric, its mode
$x_{\hat{m}}$. Now, if each m is unimodal in addition to symmetric, its mode ![]() $\tilde{x}_m$ coincides with its median
$\tilde{x}_m$ coincides with its median ![]() $Q_m\big(\frac{1}{2}\big)$, and
$Q_m\big(\frac{1}{2}\big)$, and ![]() $Q_m(\lambda y + (1-\lambda)z)\geq(\mbox{resp.} \leq)\ \lambda Q_m(y) + (1-\lambda)Q_m(z)$ for all
$Q_m(\lambda y + (1-\lambda)z)\geq(\mbox{resp.} \leq)\ \lambda Q_m(y) + (1-\lambda)Q_m(z)$ for all ![]() $y,z < (\mbox{resp.} >\!)\ \frac{1}{2}$ and
$y,z < (\mbox{resp.} >\!)\ \frac{1}{2}$ and ![]() $\lambda\in[0,1]$. Integrating these inequalities with respect to
$\lambda\in[0,1]$. Integrating these inequalities with respect to ![]() $\Pi({\mathrm{d}} m)$ and using (24), we deduce that
$\Pi({\mathrm{d}} m)$ and using (24), we deduce that ![]() $\hat{m}$ is unimodal (with mode
$\hat{m}$ is unimodal (with mode ![]() $\frac12$) too.
$\frac12$) too.
Unimodality is not preserved in general non-symmetric cases. Still, for some families of distributions unimodality is maintained after taking barycenter, as we show in the next result.
Proposition 5. If ![]() $\Pi\in\mathcal W_p(\mathcal W_\mathrm{ac}(\mathbb R))$ is concentrated on log-concave univariate distributions, then the barycenter
$\Pi\in\mathcal W_p(\mathcal W_\mathrm{ac}(\mathbb R))$ is concentrated on log-concave univariate distributions, then the barycenter ![]() $\hat{m}$ is unimodal.
$\hat{m}$ is unimodal.
Proof. If f(x) is a log-concave density, then ![]() $-\log(f(x))$ is convex and so is
$-\log(f(x))$ is convex and so is ![]() ${\mathrm{e}}^{-\log(f(x))} = {1}/{f(x)}$. Some computation reveals that
${\mathrm{e}}^{-\log(f(x))} = {1}/{f(x)}$. Some computation reveals that ![]() $f(x)\,{\mathrm{d}} x$ is unimodal for some
$f(x)\,{\mathrm{d}} x$ is unimodal for some ![]() $\tilde{x}\in\mathbb{R}$, so its quantile Q(y) is concave for
$\tilde{x}\in\mathbb{R}$, so its quantile Q(y) is concave for ![]() $y < \tilde{y}$ and convex for
$y < \tilde{y}$ and convex for ![]() $y > \tilde{y}$, where
$y > \tilde{y}$, where ![]() $Q(\tilde{y}) = \tilde{x}$. Since
$Q(\tilde{y}) = \tilde{x}$. Since ![]() ${1}/{f(x)}$ is convex decreasing for
${1}/{f(x)}$ is convex decreasing for ![]() $x < \tilde{x}$ and convex increasing for
$x < \tilde{x}$ and convex increasing for ![]() $x > \tilde{x}$,
$x > \tilde{x}$, ![]() ${1}/{f(Q(y))}$ is convex. So
${1}/{f(Q(y))}$ is convex. So ![]() $({{\mathrm{d}} Q}/{{\mathrm{d}} y})(y) = {1}/{f(Q(y))}$ is convex, positive, and with a minimum at
$({{\mathrm{d}} Q}/{{\mathrm{d}} y})(y) = {1}/{f(Q(y))}$ is convex, positive, and with a minimum at ![]() $\tilde{y}$. Given
$\tilde{y}$. Given ![]() $\Pi$, its barycenter
$\Pi$, its barycenter ![]() $\hat{m}$ satisfies
$\hat{m}$ satisfies
so if all the ![]() ${{\mathrm{d}} Q_m}/{{\mathrm{d}} y}$ are convex, then
${{\mathrm{d}} Q_m}/{{\mathrm{d}} y}$ are convex, then ![]() ${{\mathrm{d}} Q_{\hat m}}/{{\mathrm{d}} y}$ is convex and positive, with a minimum at some
${{\mathrm{d}} Q_{\hat m}}/{{\mathrm{d}} y}$ is convex and positive, with a minimum at some ![]() $\hat{y}$. Thus,
$\hat{y}$. Thus, ![]() $Q_{\hat{m}}(y)$ is concave for
$Q_{\hat{m}}(y)$ is concave for ![]() $y < \hat{y}$ and convex for
$y < \hat{y}$ and convex for ![]() $y > \hat{y}$, and
$y > \hat{y}$, and ![]() $\hat{m}$ is unimodal with a mode at
$\hat{m}$ is unimodal with a mode at ![]() $Q_{\hat{m}}(\hat{y})$.
$Q_{\hat{m}}(\hat{y})$.
Useful examples of log-concave distribution families include the general normal, exponential, logistic, Gumbel, chi-square, and Laplace laws, as well as the Weibull, power, gamma, and beta families when their shape parameters are larger than one.
6.2. Distributions sharing a common copula
If two multivariate distributions P and Q over ![]() $\mathbb{R}^q$ share the same copula, then their
$\mathbb{R}^q$ share the same copula, then their ![]() $W_p$ distance to the pth power is the sum of the
$W_p$ distance to the pth power is the sum of the ![]() $W_p(\mathbb R)$ distances between their marginals raised to the pth power. Furthermore, if the marginals of P have no atoms, then an optimal map is given by the coordinate-wise transformation
$W_p(\mathbb R)$ distances between their marginals raised to the pth power. Furthermore, if the marginals of P have no atoms, then an optimal map is given by the coordinate-wise transformation ![]() $T(x) = (T^1(x_1),\dots,T^q(x_q))$, where
$T(x) = (T^1(x_1),\dots,T^q(x_q))$, where ![]() $T^i(x_i)$ is the monotone rearrangement between the marginals
$T^i(x_i)$ is the monotone rearrangement between the marginals ![]() $P^i$ and
$P^i$ and ![]() $Q^i$ for
$Q^i$ for ![]() $i=1,\dots,q$. This setting allows us to easily extend the results from the univariate case to the multidimensional case.
$i=1,\dots,q$. This setting allows us to easily extend the results from the univariate case to the multidimensional case.
Lemma 5. If ![]() $\Pi\in\mathcal W_p(\mathcal W_\mathrm{ac}(\mathbb R^q))$ is concentrated on a set of measures sharing the same copula C, then the p-Wasserstein barycenter
$\Pi\in\mathcal W_p(\mathcal W_\mathrm{ac}(\mathbb R^q))$ is concentrated on a set of measures sharing the same copula C, then the p-Wasserstein barycenter ![]() $\hat{m}$ of
$\hat{m}$ of ![]() $\Pi$ has copula C as well, and its ith marginal
$\Pi$ has copula C as well, and its ith marginal ![]() $\hat{m}^i$ is the barycenter of the ith marginal measures of
$\hat{m}^i$ is the barycenter of the ith marginal measures of ![]() $\Pi$. In particular, the barycenter does not depend on p.
$\Pi$. In particular, the barycenter does not depend on p.
Proof. It is known [Reference Alfonsi and Jourdain3, Reference Cuesta-Albertos, Ruschendorf and Tuero-Diaz24] that for two distributions m and ![]() $\mu$ with respective ith marginals
$\mu$ with respective ith marginals ![]() $m^i$ and
$m^i$ and ![]() $\mu^i$ for
$\mu^i$ for ![]() $i=1,\ldots,q$, the p-Wasserstein metric satisfies
$i=1,\ldots,q$, the p-Wasserstein metric satisfies ![]() $W_p^p(m,\mu)\geq\sum_{i=1}^n W_p^p(m^i,\mu^i)$, where equality is reached if m and
$W_p^p(m,\mu)\geq\sum_{i=1}^n W_p^p(m^i,\mu^i)$, where equality is reached if m and ![]() $\mu$ share the same copula C (we have abused the notation, denoting by
$\mu$ share the same copula C (we have abused the notation, denoting by ![]() $W_p$ the p-Wasserstein distance on
$W_p$ the p-Wasserstein distance on ![]() $\mathbb R^q$ as well as on
$\mathbb R^q$ as well as on ![]() $\mathbb R$). Thus,
$\mathbb R$). Thus,
where ![]() $\Pi^i$ is defined via the identity
$\Pi^i$ is defined via the identity ![]() $\int_{\mathcal P(\mathbb R)}f(\nu)\,\Pi^i({\mathrm{d}}\nu) = \int_{\mathcal P(\mathbb R^q)}f(m^i)\,\Pi({\mathrm{d}} m)$. The infimum for the lower bound is reached on the univariate measures
$\int_{\mathcal P(\mathbb R)}f(\nu)\,\Pi^i({\mathrm{d}}\nu) = \int_{\mathcal P(\mathbb R^q)}f(m^i)\,\Pi({\mathrm{d}} m)$. The infimum for the lower bound is reached on the univariate measures ![]() $\hat{m}^1,\ldots,\hat{m}^q$ where
$\hat{m}^1,\ldots,\hat{m}^q$ where ![]() $\hat{m}^i$ is the p-barycenter of
$\hat{m}^i$ is the p-barycenter of ![]() $\Pi^i$, which means that
$\Pi^i$, which means that ![]() $\hat{m}^i = \mathrm{argmin}\int W_p^p(\nu,\mu^i)\,\Pi^i({\mathrm{d}}\nu)$. It is plain that the infimum is reached on the distribution
$\hat{m}^i = \mathrm{argmin}\int W_p^p(\nu,\mu^i)\,\Pi^i({\mathrm{d}}\nu)$. It is plain that the infimum is reached on the distribution ![]() $\hat{m}$ with copula C and ith marginal
$\hat{m}$ with copula C and ith marginal ![]() $\hat{m}^i$ for
$\hat{m}^i$ for ![]() $i=1,\ldots,q$, which then has to be the barycenter of
$i=1,\ldots,q$, which then has to be the barycenter of ![]() $\Pi$ and is independent of p.
$\Pi$ and is independent of p.
A Wasserstein SGD iteration, starting from a distribution ![]() $\mu$, sampling
$\mu$, sampling ![]() $m \sim \Pi$, and with step
$m \sim \Pi$, and with step ![]() $\gamma$, both
$\gamma$, both ![]() $\mu$ and m having copula C, produces the measure
$\mu$ and m having copula C, produces the measure ![]() $\nu = ((1-\gamma)I + \gamma T_\mu^m)(\mu)$ characterized by having copula C and the ith marginal quantile functions
$\nu = ((1-\gamma)I + \gamma T_\mu^m)(\mu)$ characterized by having copula C and the ith marginal quantile functions ![]() $Q_{\nu^i}(\!\cdot\!) = (1-\gamma)Q_{\mu^i}(\!\cdot\!) + \gamma Q_{m^i}(\!\cdot\!)$ for
$Q_{\nu^i}(\!\cdot\!) = (1-\gamma)Q_{\mu^i}(\!\cdot\!) + \gamma Q_{m^i}(\!\cdot\!)$ for ![]() $i=1,\dots,q$. The BSGD iteration works analogously. Alternatively, we can perform (batch) stochastic gradient descent component-wise (with respect to the marginals
$i=1,\dots,q$. The BSGD iteration works analogously. Alternatively, we can perform (batch) stochastic gradient descent component-wise (with respect to the marginals ![]() $\Pi^i$ of
$\Pi^i$ of ![]() $\Pi$) and then make use of the copula C. As in the one-dimensional case, the barycenter is in this case automatically pseudo-associative since it is associative. Bounds for the expected optimality gap and in
$\Pi$) and then make use of the copula C. As in the one-dimensional case, the barycenter is in this case automatically pseudo-associative since it is associative. Bounds for the expected optimality gap and in ![]() $W_2^2$ for the SGD sequence can be similarly deduced in this case too.
$W_2^2$ for the SGD sequence can be similarly deduced in this case too.
6.3. Spherically equivalent distributions
We denote here by ![]() $\mathcal{L}(\!\cdot\!)$ the law of a random vector, so
$\mathcal{L}(\!\cdot\!)$ the law of a random vector, so ![]() $m=\mathcal L(x)$ and
$m=\mathcal L(x)$ and ![]() $x\sim m$ are synonyms. Following [Reference Cuesta-Albertos, Ruschendorf and Tuero-Diaz24], another multidimensional case is constructed as follows: Given a fixed measure
$x\sim m$ are synonyms. Following [Reference Cuesta-Albertos, Ruschendorf and Tuero-Diaz24], another multidimensional case is constructed as follows: Given a fixed measure ![]() $\tilde{m} \in \mathcal{W}_{2,\mathrm{ac}}(\mathbb{R}^q)$, its associated family of spherically equivalent distributions is
$\tilde{m} \in \mathcal{W}_{2,\mathrm{ac}}(\mathbb{R}^q)$, its associated family of spherically equivalent distributions is
where ![]() $\|\cdot\|_2$ is the Euclidean norm and
$\|\cdot\|_2$ is the Euclidean norm and ![]() $\mathcal{ND}(\mathbb{R})$ is the set of non-decreasing non-negative functions of
$\mathcal{ND}(\mathbb{R})$ is the set of non-decreasing non-negative functions of ![]() $\mathbb R_+$. These types of distributions include the simplicially contoured distributions, and also elliptical distributions with the same correlation structure.
$\mathbb R_+$. These types of distributions include the simplicially contoured distributions, and also elliptical distributions with the same correlation structure.
If ![]() $y \sim m \in \mathcal{S}_0$, then
$y \sim m \in \mathcal{S}_0$, then ![]() $\alpha(r) = Q_{\|y\|_2}(F_{\|\tilde{x}\|_2}(r))$, where
$\alpha(r) = Q_{\|y\|_2}(F_{\|\tilde{x}\|_2}(r))$, where ![]() $Q_{\|y\|_2}$ is the quantile function of the norm of y,
$Q_{\|y\|_2}$ is the quantile function of the norm of y, ![]() $F_{\|\tilde{x}\|_2}$ is the distribution function of the norm of
$F_{\|\tilde{x}\|_2}$ is the distribution function of the norm of ![]() $\tilde{x}$, and
$\tilde{x}$, and
More generally, if
then the optimal transport from ![]() $m_1$ to
$m_1$ to ![]() $m_2$ is given by
$m_2$ is given by
where ![]() $\alpha(r)=Q_{\|x_2\|_2}(F_{\|x_1\|_2}(r))$. Since
$\alpha(r)=Q_{\|x_2\|_2}(F_{\|x_1\|_2}(r))$. Since ![]() $F_{\|x_1\|_2}(r)=F_{\|\tilde{x}\|_2}(\alpha_1^{-1}(r))$ and
$F_{\|x_1\|_2}(r)=F_{\|\tilde{x}\|_2}(\alpha_1^{-1}(r))$ and ![]() $Q_{\|x_2\|_2}(r)=\alpha_2(Q_{\|\tilde{x}\|_2}(r))$, we see that
$Q_{\|x_2\|_2}(r)=\alpha_2(Q_{\|\tilde{x}\|_2}(r))$, we see that ![]() $\alpha(r) =\alpha_2(Q_{\|\tilde{x}\|_2}(F_{\|\tilde{x}\|_2}(\alpha_1^{-1}(r)))) = \alpha_2(\alpha_1^{-1}(r))$, so finally
$\alpha(r) =\alpha_2(Q_{\|\tilde{x}\|_2}(F_{\|\tilde{x}\|_2}(\alpha_1^{-1}(r)))) = \alpha_2(\alpha_1^{-1}(r))$, so finally
Note that these kinds of transports are closed under composition and convex combination, and contain the identity. An SGD iteration, starting from a distribution
sampling
with step ![]() $\gamma$, produces
$\gamma$, produces ![]() $m_1 =T_0^{\gamma,m}(\mu)\;:\!=\; ((1-\gamma)I + \gamma T_\mu^m)(\mu)$. Since
$m_1 =T_0^{\gamma,m}(\mu)\;:\!=\; ((1-\gamma)I + \gamma T_\mu^m)(\mu)$. Since
we have
with ![]() $\alpha_1 = \gamma\alpha + (1-\gamma)\alpha_0$. Analogously, the batch stochastic gradient iteration produces
$\alpha_1 = \gamma\alpha + (1-\gamma)\alpha_0$. Analogously, the batch stochastic gradient iteration produces ![]() $\alpha_{1}=(1-\gamma)\alpha_0+({\gamma}/{S})\sum_{i=1}^{S}\alpha_{m^{i}}$. Note that these iterations live in
$\alpha_{1}=(1-\gamma)\alpha_0+({\gamma}/{S})\sum_{i=1}^{S}\alpha_{m^{i}}$. Note that these iterations live in ![]() $\mathcal{S}_0$, and thus the barycenter
$\mathcal{S}_0$, and thus the barycenter ![]() $\hat{m} \in \mathcal{S}_0$.
$\hat{m} \in \mathcal{S}_0$.
For the barycenter
the equation ![]() $\int T_{\hat{m}}^{m}(x)\,\Pi({\mathrm{d}} m) = x$ can be expressed as
$\int T_{\hat{m}}^{m}(x)\,\Pi({\mathrm{d}} m) = x$ can be expressed as ![]() $\hat{\alpha}(r) = \int\alpha_m(r)\,\Pi({\mathrm{d}} m)$, or equivalently
$\hat{\alpha}(r) = \int\alpha_m(r)\,\Pi({\mathrm{d}} m)$, or equivalently ![]() $Q^{\hat{m}}_{\|\hat{y}\|_2}(p) = \int Q^m_{\|y\|_2}(p)\,\Pi({\mathrm{d}} m)$, where
$Q^{\hat{m}}_{\|\hat{y}\|_2}(p) = \int Q^m_{\|y\|_2}(p)\,\Pi({\mathrm{d}} m)$, where ![]() $Q^m_{\|y\|_2}$ is the quantile function of the norm of
$Q^m_{\|y\|_2}$ is the quantile function of the norm of ![]() $y \sim m$. This is similar to the univariate setting and, as in that case, the barycenter is associative, and convergence bounds for the optimality gap and the SDG sequence can be established.
$y \sim m$. This is similar to the univariate setting and, as in that case, the barycenter is associative, and convergence bounds for the optimality gap and the SDG sequence can be established.
6.4. Scatter-location family
We borrow here the setting of [Reference Álvarez-Esteban, del Barrio, Cuesta-Albertos and Matrán5], where another useful multidimensional case is defined as follows: Given a fixed distribution ![]() $\tilde{m} \in \mathcal{W}_{2,\mathrm{ac}}(\mathbb{R}^q)$, referred to as the generator, the generated scatter-location family is given by
$\tilde{m} \in \mathcal{W}_{2,\mathrm{ac}}(\mathbb{R}^q)$, referred to as the generator, the generated scatter-location family is given by
where ![]() $\mathcal{M}_+^{q\times q}$ is the set of symmetric positive-definite matrices of size
$\mathcal{M}_+^{q\times q}$ is the set of symmetric positive-definite matrices of size ![]() $q\times q$. Without loss of generality we can assume that
$q\times q$. Without loss of generality we can assume that ![]() $\tilde{m}$ has zero mean and identity covariance. A clear example is the multivariate Gaussian family
$\tilde{m}$ has zero mean and identity covariance. A clear example is the multivariate Gaussian family ![]() $\mathcal{F}(\tilde{m})$, with
$\mathcal{F}(\tilde{m})$, with ![]() $\tilde{m}$ a standard multivariate normal distribution.
$\tilde{m}$ a standard multivariate normal distribution.
The optimal transport between two members of ![]() $\mathcal{F}(\tilde{m})$ is explicit. If
$\mathcal{F}(\tilde{m})$ is explicit. If ![]() $m_1 = \mathcal{L}(A_1\tilde{x}+b_1)$ and
$m_1 = \mathcal{L}(A_1\tilde{x}+b_1)$ and ![]() $m_2 = \mathcal{L}(A_2\tilde{x}+b_2)$ then the optimal map from
$m_2 = \mathcal{L}(A_2\tilde{x}+b_2)$ then the optimal map from ![]() $m_1$ to
$m_1$ to ![]() $m_2$ is given by
$m_2$ is given by ![]() $T_{m_1}^{m_2}(x) = A(x-b_1) + b_2$, where
$T_{m_1}^{m_2}(x) = A(x-b_1) + b_2$, where ![]() $A = A_1^{-1}(A_1A_2^2A_1)^{1/2}A_1^{-1} \in \mathcal{M}_+^{q\times q}$. The family
$A = A_1^{-1}(A_1A_2^2A_1)^{1/2}A_1^{-1} \in \mathcal{M}_+^{q\times q}$. The family ![]() $\mathcal{F}(\tilde{m})$ is therefore geodesically closed.
$\mathcal{F}(\tilde{m})$ is therefore geodesically closed.
If ![]() $\Pi$ is supported on
$\Pi$ is supported on ![]() $\mathcal{F}(\tilde{m})$, then its 2-Wasserstein barycenter
$\mathcal{F}(\tilde{m})$, then its 2-Wasserstein barycenter ![]() $\hat{m}$ belongs to
$\hat{m}$ belongs to ![]() $\mathcal{F}(\tilde{m})$. Call its mean
$\mathcal{F}(\tilde{m})$. Call its mean ![]() $\hat{b}$ and its covariance matrix
$\hat{b}$ and its covariance matrix ![]() $\hat{\Sigma}$. Since the optimal map from
$\hat{\Sigma}$. Since the optimal map from ![]() $\hat{m}$ to m is
$\hat{m}$ to m is ![]() $T_{\hat{m}}^{m}(x) = A_{\hat{m}}^{m}(x-\hat{b}) + b_m$ where
$T_{\hat{m}}^{m}(x) = A_{\hat{m}}^{m}(x-\hat{b}) + b_m$ where ![]() $A_{\hat{m}}^{m} = \hat{\Sigma}^{-1/2}(\hat{\Sigma}^{1/2}\Sigma_m\hat{\Sigma}^{1/2})^{1/2}\hat{\Sigma}^{-1/2}$, and we know that
$A_{\hat{m}}^{m} = \hat{\Sigma}^{-1/2}(\hat{\Sigma}^{1/2}\Sigma_m\hat{\Sigma}^{1/2})^{1/2}\hat{\Sigma}^{-1/2}$, and we know that ![]() $\hat{m}$-almost surely
$\hat{m}$-almost surely ![]() $\int T_{\hat{m}}^{m}(x)\,\Pi({\mathrm{d}} m) = x$, then we must have
$\int T_{\hat{m}}^{m}(x)\,\Pi({\mathrm{d}} m) = x$, then we must have ![]() $\int A_{\hat{m}}^{m}\,\Pi({\mathrm{d}} m) = I$, since clearly
$\int A_{\hat{m}}^{m}\,\Pi({\mathrm{d}} m) = I$, since clearly ![]() $\hat{b}=\int b_m\,\Pi({\mathrm{d}} m)$. As a consequence, we have
$\hat{b}=\int b_m\,\Pi({\mathrm{d}} m)$. As a consequence, we have ![]() $\hat{\Sigma} = \int(\hat{\Sigma}^{1/2}\Sigma_m\hat{\Sigma}^{1/2})^{1/2}\,\Pi({\mathrm{d}} m)$.
$\hat{\Sigma} = \int(\hat{\Sigma}^{1/2}\Sigma_m\hat{\Sigma}^{1/2})^{1/2}\,\Pi({\mathrm{d}} m)$.
A stochastic gradient descent iteration, starting from a distribution ![]() $\mu = \mathcal{L}(A_0\tilde{x}+b_0)$, sampling some
$\mu = \mathcal{L}(A_0\tilde{x}+b_0)$, sampling some ![]() $m=\mathcal{L}(A_m\tilde{x}+b_m) \sim \Pi$, and with step
$m=\mathcal{L}(A_m\tilde{x}+b_m) \sim \Pi$, and with step ![]() $\gamma$, produces the measure
$\gamma$, produces the measure ![]() $\nu=T_0^{\gamma,m}(\mu)\;:\!=\; \big((1-\gamma)I + \gamma T_\mu^m\big)(\mu)$. If
$\nu=T_0^{\gamma,m}(\mu)\;:\!=\; \big((1-\gamma)I + \gamma T_\mu^m\big)(\mu)$. If ![]() $\tilde{x}$ has a multivariate distribution
$\tilde{x}$ has a multivariate distribution ![]() $\tilde{F}(x)$, then
$\tilde{F}(x)$, then ![]() $\mu$ has distribution
$\mu$ has distribution ![]() $F_0(x)=\tilde{F}(A_0^{-1}(x-b_0))$ with mean
$F_0(x)=\tilde{F}(A_0^{-1}(x-b_0))$ with mean ![]() $b_0$ and covariance
$b_0$ and covariance ![]() $\Sigma_0 = A_0^2$. We have
$\Sigma_0 = A_0^2$. We have ![]() $T_0^{\gamma,m}(x) = ((1-\gamma)I + \gamma A_{\mu}^{m})(x-b_0) + \gamma b_m + (1-\gamma)b_0$ with
$T_0^{\gamma,m}(x) = ((1-\gamma)I + \gamma A_{\mu}^{m})(x-b_0) + \gamma b_m + (1-\gamma)b_0$ with ![]() $A_{\mu}^{m} \;:\!=\; A_0^{-1}(A_0A_m^2A_0)^{1/2}A_0^{-1}$. Then
$A_{\mu}^{m} \;:\!=\; A_0^{-1}(A_0A_m^2A_0)^{1/2}A_0^{-1}$. Then
with mean ![]() $b_1 = (1-\gamma)b_0 + \gamma b_m$ and covariance
$b_1 = (1-\gamma)b_0 + \gamma b_m$ and covariance
 \begin{align*} \Sigma_1 = A_1^2 & = \big[(1-\gamma)A_0+\gamma A_0^{-1}\big(A_0A_m^2A_0\big)^{1/2}\big] \big[(1-\gamma)A_0+\gamma\big(A_0A_m^2A_0\big)^{1/2}A_0^{-1}\big] \\[5pt] & = A_0^{-1}\big[(1-\gamma)A_0^2+\gamma\big(A_0A_m^2A_0\big)^{1/2}\big] \big[(1-\gamma)A_0^2+\gamma\big(A_0A_m^2A_0\big)^{1/2}\big]A_0^{-1} \\[5pt] & = A_0^{-1}\big[(1-\gamma)A_0^2+\gamma\big(A_0A_m^2A_0\big)^{1/2}\big]^2A_0^{-1}.\end{align*}
\begin{align*} \Sigma_1 = A_1^2 & = \big[(1-\gamma)A_0+\gamma A_0^{-1}\big(A_0A_m^2A_0\big)^{1/2}\big] \big[(1-\gamma)A_0+\gamma\big(A_0A_m^2A_0\big)^{1/2}A_0^{-1}\big] \\[5pt] & = A_0^{-1}\big[(1-\gamma)A_0^2+\gamma\big(A_0A_m^2A_0\big)^{1/2}\big] \big[(1-\gamma)A_0^2+\gamma\big(A_0A_m^2A_0\big)^{1/2}\big]A_0^{-1} \\[5pt] & = A_0^{-1}\big[(1-\gamma)A_0^2+\gamma\big(A_0A_m^2A_0\big)^{1/2}\big]^2A_0^{-1}.\end{align*}
The batch stochastic gradient descent iteration is characterized by
 \begin{equation*} b_{1} = (1-\gamma)b_0+\frac{\gamma}{S}\sum_{i=1}^{S}b_{m^{i}}, \qquad A_{1}^2 = A_0^{-1}\Bigg[(1-\gamma)A_0^2+\frac{\gamma}{S}\sum_{i=1}^{S}\big(A_0A_{m^{i}}^2A_0\big)^{1/2}\Bigg]^2A_0^{-1}.\end{equation*}
\begin{equation*} b_{1} = (1-\gamma)b_0+\frac{\gamma}{S}\sum_{i=1}^{S}b_{m^{i}}, \qquad A_{1}^2 = A_0^{-1}\Bigg[(1-\gamma)A_0^2+\frac{\gamma}{S}\sum_{i=1}^{S}\big(A_0A_{m^{i}}^2A_0\big)^{1/2}\Bigg]^2A_0^{-1}.\end{equation*}
Notice that if all the matrices ![]() $\{A_m\colon m\in\text{supp}(\Pi)\}$ share the same eigenspaces, then the barycenter is pseudo-associative, as it is in fact associative. In the case that these matrices do not necessarily share the same eigenspaces, and
$\{A_m\colon m\in\text{supp}(\Pi)\}$ share the same eigenspaces, then the barycenter is pseudo-associative, as it is in fact associative. In the case that these matrices do not necessarily share the same eigenspaces, and ![]() $\tilde m$ is Gaussian, it is still possible to give conditions under which the barycenter is pseudo-associative: as we have already mentioned, this property holds in the setting of [Reference Chewi, Maunu, Rigollet and Stromme19] under conditions of uniform boundedness and uniform positivity of covariance matrices.
$\tilde m$ is Gaussian, it is still possible to give conditions under which the barycenter is pseudo-associative: as we have already mentioned, this property holds in the setting of [Reference Chewi, Maunu, Rigollet and Stromme19] under conditions of uniform boundedness and uniform positivity of covariance matrices.
Appendix A. Some remarks in the case of general measures
We discuss a natural counterpart to the SGD sequence in the case where ![]() $\Pi$ is not necessarily supported on absolutely continuous measures. However, in this case we neither have a verifiable result guaranteeing the convergence of the SGD method, nor a verifiable result saying that the accumulation points of the SGD sequence are necessarily Karcher means. The goal of this section is to introduce the objects needed for an analysis of the general case, to advance the convergence analysis as much as possible, and to illustrate the difficulties that we encounter that make us stop short of obtaining general convergence results.
$\Pi$ is not necessarily supported on absolutely continuous measures. However, in this case we neither have a verifiable result guaranteeing the convergence of the SGD method, nor a verifiable result saying that the accumulation points of the SGD sequence are necessarily Karcher means. The goal of this section is to introduce the objects needed for an analysis of the general case, to advance the convergence analysis as much as possible, and to illustrate the difficulties that we encounter that make us stop short of obtaining general convergence results.
While we retain Assumption 1, we modify Assumption 2 into the following.
Assumption 2′′. ![]() $\Pi = \sum_{j=1}^\ell\lambda_j\delta_{\nu_j}$, with each
$\Pi = \sum_{j=1}^\ell\lambda_j\delta_{\nu_j}$, with each ![]() $\nu_j\in\mathcal W_2(\mathcal X)$ and where the
$\nu_j\in\mathcal W_2(\mathcal X)$ and where the ![]() $\lambda_j\in(0,1)$ sum to 1.
$\lambda_j\in(0,1)$ sum to 1.
Remark 5. We can find ![]() $V\colon\mathcal X\to[0,\infty)$ convex, continuous, and super-quadratic (i.e.
$V\colon\mathcal X\to[0,\infty)$ convex, continuous, and super-quadratic (i.e. ![]() $\lim_{|y|\to\infty}V(y)/|y|^2=+\infty$) and
$\lim_{|y|\to\infty}V(y)/|y|^2=+\infty$) and ![]() $C\in(0,\infty)$ such that
$C\in(0,\infty)$ such that ![]() $\int V\,{\mathrm{d}}\nu_j\leq C$ for each j. Defining
$\int V\,{\mathrm{d}}\nu_j\leq C$ for each j. Defining
it follows that ![]() $K_\Pi$ is compact in
$K_\Pi$ is compact in ![]() $\mathcal W_2(\mathcal X)$ and
$\mathcal W_2(\mathcal X)$ and ![]() $\Pi(K_\Pi)=1$. Moreover, if (X,Y) is any optimal coupling with marginals
$\Pi(K_\Pi)=1$. Moreover, if (X,Y) is any optimal coupling with marginals ![]() $\mu$ and
$\mu$ and ![]() $\nu$, with
$\nu$, with ![]() $\mu$ and
$\mu$ and ![]() $\nu$ in
$\nu$ in ![]() $K_\Pi$, then also
$K_\Pi$, then also ![]() $\text{Law}(tX+(1-t)Y)\in K_\Pi$ for each
$\text{Law}(tX+(1-t)Y)\in K_\Pi$ for each ![]() $t\in(0,1)$. In the following, we denote by
$t\in(0,1)$. In the following, we denote by ![]() $K_\Pi$ a set with these properties which may or may not be given explicitly as in (25).
$K_\Pi$ a set with these properties which may or may not be given explicitly as in (25).
Throughout, we denote by ![]() $\textsf{Opt}(\mu,\nu)$ the set of optimal couplings attaining the infimum defining
$\textsf{Opt}(\mu,\nu)$ the set of optimal couplings attaining the infimum defining ![]() $W_2(\mu,\nu)$, which is non-empty and may contain multiple elements, and we fix
$W_2(\mu,\nu)$, which is non-empty and may contain multiple elements, and we fix
a measurable selection of optimal couplings. In practical terms an algorithm for computing or approximating optimal couplings would be automatically measurable.
Definition 7. Let ![]() $\mu_0 \in K_\Pi$,
$\mu_0 \in K_\Pi$, ![]() $m_k \stackrel{\mathrm{i.i.d.}}{\sim}\Pi$, and
$m_k \stackrel{\mathrm{i.i.d.}}{\sim}\Pi$, and ![]() $\gamma_k > 0$ for
$\gamma_k > 0$ for ![]() $k \geq 0$. We define the SGD sequence by
$k \geq 0$. We define the SGD sequence by
where ![]() $\text{Law}(X,Y)=G(\mu_k,m_k)$.
$\text{Law}(X,Y)=G(\mu_k,m_k)$.
By Remark 5 we have ![]() $\{\mu_k\colon k\in\mathbb N\}\subset K_\Pi$ (almost surely).
$\{\mu_k\colon k\in\mathbb N\}\subset K_\Pi$ (almost surely).
Definition 8. ![]() $\mu\in\mathcal W_2(\mathcal X)$ is a Karcher mean of
$\mu\in\mathcal W_2(\mathcal X)$ is a Karcher mean of ![]() $\Pi$ if,
$\Pi$ if, ![]() $\mu({\mathrm{d}} x)$-almost surely,
$\mu({\mathrm{d}} x)$-almost surely, ![]() $x=\sum_{j=1}^\ell \lambda_j \mathbb E[Y_j\mid X=x]$, where (for each j)
$x=\sum_{j=1}^\ell \lambda_j \mathbb E[Y_j\mid X=x]$, where (for each j) ![]() $\text{Law}(X,Y_j)$ is some coupling in
$\text{Law}(X,Y_j)$ is some coupling in ![]() $\textsf{Opt}(\mu,\nu_j)$.
$\textsf{Opt}(\mu,\nu_j)$.
We first observe that if ![]() $\mu$ is absolutely continuous, then it is a Karcher mean according to Definition 8 if and only if it is a Karcher mean according to Definition 3. On the other hand, if
$\mu$ is absolutely continuous, then it is a Karcher mean according to Definition 8 if and only if it is a Karcher mean according to Definition 3. On the other hand, if ![]() $\mu$ is a barycenter of
$\mu$ is a barycenter of ![]() $\Pi$ then it is also a Karcher mean according to Definition 8. Indeed, if
$\Pi$ then it is also a Karcher mean according to Definition 8. Indeed, if ![]() $\text{Law}(X,Y_j)\in\textsf{Opt}(\mu,\nu_j)$ and we couple all these random variables in the same probability space, then
$\text{Law}(X,Y_j)\in\textsf{Opt}(\mu,\nu_j)$ and we couple all these random variables in the same probability space, then
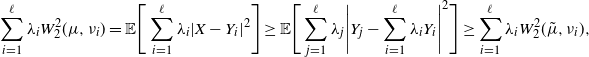 \begin{equation*} \sum_{i=1}^\ell\lambda_i W_2^2(\mu,\nu_i) = \mathbb E\Bigg[\sum_{i=1}^\ell\lambda_i|X-Y_i|^2\Bigg] \geq \mathbb E\Bigg[\sum_{j=1}^\ell\lambda_j\Bigg|Y_j-\sum_{i=1}^\ell\lambda_i Y_i\Bigg|^2\Bigg] \geq \sum_{i=1}^\ell\lambda_i W_2^2(\tilde\mu,\nu_i),\end{equation*}
\begin{equation*} \sum_{i=1}^\ell\lambda_i W_2^2(\mu,\nu_i) = \mathbb E\Bigg[\sum_{i=1}^\ell\lambda_i|X-Y_i|^2\Bigg] \geq \mathbb E\Bigg[\sum_{j=1}^\ell\lambda_j\Bigg|Y_j-\sum_{i=1}^\ell\lambda_i Y_i\Bigg|^2\Bigg] \geq \sum_{i=1}^\ell\lambda_i W_2^2(\tilde\mu,\nu_i),\end{equation*}
so the inequalities above must be actual equalities and we have ![]() $\mu=\text{Law}(\sum_i\lambda_i Y_i)\;:\!=\;\tilde\mu$ as well as
$\mu=\text{Law}(\sum_i\lambda_i Y_i)\;:\!=\;\tilde\mu$ as well as ![]() $X=\sum_i\lambda_i Y_i$ (almost surely). Taking conditional expectation with respect to X in the latter, we conclude.
$X=\sum_i\lambda_i Y_i$ (almost surely). Taking conditional expectation with respect to X in the latter, we conclude.
In direct analogy to the absolutely continuous case, we write ![]() $F(\mu)\;:\!=\;\frac{1}{2}\sum_j\lambda_j W_2^2(\mu,\nu_j)$, and we introduce
$F(\mu)\;:\!=\;\frac{1}{2}\sum_j\lambda_j W_2^2(\mu,\nu_j)$, and we introduce ![]() $F'(\mu)(x)\;:\!=\;x-\sum_{j=1}^\ell\lambda_j\mathbb E[Y_j\mid X=x]$, where
$F'(\mu)(x)\;:\!=\;x-\sum_{j=1}^\ell\lambda_j\mathbb E[Y_j\mid X=x]$, where ![]() $(X,Y_j)\sim G(\mu,\nu_j)$. With this notation we have the implication that
$(X,Y_j)\sim G(\mu,\nu_j)$. With this notation we have the implication that ![]() $\|F'(\mu)\|_{L^2(\mu)}=0 \Rightarrow \mu $ is a Karcher mean. As before, we denote by
$\|F'(\mu)\|_{L^2(\mu)}=0 \Rightarrow \mu $ is a Karcher mean. As before, we denote by ![]() $\mathcal F_{0}$ the trivial sigma-algebra and
$\mathcal F_{0}$ the trivial sigma-algebra and ![]() $\mathcal F_{k+1}$,
$\mathcal F_{k+1}$, ![]() $k\geq 0$, the sigma-algebra generated by
$k\geq 0$, the sigma-algebra generated by ![]() $m_0,\dots,m_{k}$.
$m_0,\dots,m_{k}$.
Proposition 6. The SGD sequence in (26) satisfies, almost surely,
Proof. We can define a coupling ![]() $(X_k,Y_k,Z_i)$ such that
$(X_k,Y_k,Z_i)$ such that ![]() $\text{Law}(X_k,Y_k)\in G(\mu_k,m_k)$,
$\text{Law}(X_k,Y_k)\in G(\mu_k,m_k)$, ![]() $\text{Law}(X_k,Z_i)\in G(\mu_k,\nu_i)$, and where
$\text{Law}(X_k,Z_i)\in G(\mu_k,\nu_i)$, and where ![]() $Y_k$ and
$Y_k$ and ![]() $Z_i$ are independent conditionally on
$Z_i$ are independent conditionally on ![]() $\mathcal F_k$. Then the coupling
$\mathcal F_k$. Then the coupling ![]() $((1-\gamma_k)X_k+\gamma_k Y_k,Z_i)$ has first marginal
$((1-\gamma_k)X_k+\gamma_k Y_k,Z_i)$ has first marginal ![]() $\mu_{k+1}$ and second marginal
$\mu_{k+1}$ and second marginal ![]() $\nu_i$. We compute
$\nu_i$. We compute
 \begin{align*} W_2^2(\mu_{k+1},\nu_i) & \leq \mathbb E[|(1-\gamma_k)X_k+\gamma_k Y_k-Z_i|^2] \\[5pt] & = \mathbb E[|X_k-Z_i|^2] - 2\gamma_k\mathbb E[\langle X_k-Z_i, X_k-Y_k\rangle] + \gamma_k^2\mathbb E[|X_k-Y_k|^2]. \end{align*}
\begin{align*} W_2^2(\mu_{k+1},\nu_i) & \leq \mathbb E[|(1-\gamma_k)X_k+\gamma_k Y_k-Z_i|^2] \\[5pt] & = \mathbb E[|X_k-Z_i|^2] - 2\gamma_k\mathbb E[\langle X_k-Z_i, X_k-Y_k\rangle] + \gamma_k^2\mathbb E[|X_k-Y_k|^2]. \end{align*}
Hence,
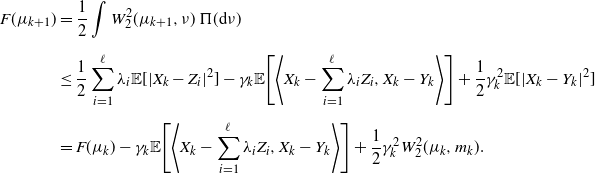 \begin{align*} F(\mu_{k+1}) & = \frac{1}{2}\int W_{2}^2(\mu_{k+1},\nu)\,\Pi({\mathrm{d}}\nu) \\[5pt] & \leq \frac{1}{2}\sum_{i=1}^\ell\lambda_i\mathbb E[|X_k-Z_i|^2] - \gamma_k\mathbb E\Bigg[\Bigg\langle X_k- \sum_{i=1}^\ell\lambda_i Z_i,X_k-Y_k\Bigg\rangle\Bigg] + \frac{1}{2}\gamma_k^2\mathbb E[|X_k-Y_k|^2] \\[5pt] & = F(\mu_k) - \gamma_k\mathbb E\Bigg[\Bigg\langle X_k-\sum_{i=1}^\ell\lambda_i Z_i,X_k-Y_k\Bigg\rangle\Bigg] + \frac{1}{2}\gamma_k^2 W_2^2(\mu_k,m_k). \end{align*}
\begin{align*} F(\mu_{k+1}) & = \frac{1}{2}\int W_{2}^2(\mu_{k+1},\nu)\,\Pi({\mathrm{d}}\nu) \\[5pt] & \leq \frac{1}{2}\sum_{i=1}^\ell\lambda_i\mathbb E[|X_k-Z_i|^2] - \gamma_k\mathbb E\Bigg[\Bigg\langle X_k- \sum_{i=1}^\ell\lambda_i Z_i,X_k-Y_k\Bigg\rangle\Bigg] + \frac{1}{2}\gamma_k^2\mathbb E[|X_k-Y_k|^2] \\[5pt] & = F(\mu_k) - \gamma_k\mathbb E\Bigg[\Bigg\langle X_k-\sum_{i=1}^\ell\lambda_i Z_i,X_k-Y_k\Bigg\rangle\Bigg] + \frac{1}{2}\gamma_k^2 W_2^2(\mu_k,m_k). \end{align*}
Taking conditional expectation with respect to ![]() $\mathcal F_k$, and as
$\mathcal F_k$, and as ![]() $m_k$ is independently sampled from this sigma-algebra, we see that
$m_k$ is independently sampled from this sigma-algebra, we see that
 $$\mathbb E[W_2^2(\mu_k,m_k)\mid\mathcal F_k] = \sum_{i=1}^\ell\lambda_i W_2^2(\mu_k,\nu_i) = 2F(\mu_k).$$
$$\mathbb E[W_2^2(\mu_k,m_k)\mid\mathcal F_k] = \sum_{i=1}^\ell\lambda_i W_2^2(\mu_k,\nu_i) = 2F(\mu_k).$$
Similarly, we have
 $$\mathbb E\Bigg[\mathbb E\Bigg[\Bigg\langle X_k-\sum_{i=1}^\ell\lambda_i Z_i, X_k-Y_k\Bigg\rangle\Bigg] \mid \mathcal F_k\Bigg] = \mathbb E\Bigg[\Bigg\langle X_k-\sum_{i=1}^\ell\lambda_i\mathbb E[Z_i\mid X_k], X_k-\sum_{i=1}^\ell\lambda_i \mathbb E[Y_i\mid X_k]\Bigg\rangle\Bigg]. $$
$$\mathbb E\Bigg[\mathbb E\Bigg[\Bigg\langle X_k-\sum_{i=1}^\ell\lambda_i Z_i, X_k-Y_k\Bigg\rangle\Bigg] \mid \mathcal F_k\Bigg] = \mathbb E\Bigg[\Bigg\langle X_k-\sum_{i=1}^\ell\lambda_i\mathbb E[Z_i\mid X_k], X_k-\sum_{i=1}^\ell\lambda_i \mathbb E[Y_i\mid X_k]\Bigg\rangle\Bigg]. $$
We conclude that ![]() $\mathbb{E}[F(\mu_{k+1})\mid\mathcal F_k]\leq(1+\gamma_k^2)F(\mu_k)-\gamma_k\|F^\prime(\mu_k)\|^2_{L^2(\mu_k)}$.
$\mathbb{E}[F(\mu_{k+1})\mid\mathcal F_k]\leq(1+\gamma_k^2)F(\mu_k)-\gamma_k\|F^\prime(\mu_k)\|^2_{L^2(\mu_k)}$.
The next lemma is the only part where we use that ![]() $\Pi$ is supported in finitely many measures. With more refined arguments we could surely avoid this limitation.
$\Pi$ is supported in finitely many measures. With more refined arguments we could surely avoid this limitation.
Lemma 6. Let ![]() $(\rho_n)_n \subset \mathcal{W}_{2}(\mathbb{R}^q)$ be a sequence converging with respect to
$(\rho_n)_n \subset \mathcal{W}_{2}(\mathbb{R}^q)$ be a sequence converging with respect to ![]() $W_2$ to
$W_2$ to ![]() $\rho\in\mathcal{W}_{2}(\mathbb{R}^q)$. Then, as
$\rho\in\mathcal{W}_{2}(\mathbb{R}^q)$. Then, as ![]() $n\to\infty$,
$n\to\infty$,
(i)
 $F(\rho_n)\to F(\rho)$;
$F(\rho_n)\to F(\rho)$;-
(ii)
 $\|F'(\rho_n)\|_{L^2(\rho_n)}\to 0$ implies that
$\|F'(\rho_n)\|_{L^2(\rho_n)}\to 0$ implies that  $\rho$ is a Karcher mean.
$\rho$ is a Karcher mean.
Proof. Part (i) is immediate since ![]() $W_2(\rho_n,\nu_j)\to W_2(\rho,\nu_j)$ for each j. For part (ii), we first observe that
$W_2(\rho_n,\nu_j)\to W_2(\rho,\nu_j)$ for each j. For part (ii), we first observe that ![]() $G(\rho_n,\nu_j)$ is tight for each j. Passing to a subsequence if necessary, the Skorokhod representation theorem yields, on some probability space, a sequence of random variables
$G(\rho_n,\nu_j)$ is tight for each j. Passing to a subsequence if necessary, the Skorokhod representation theorem yields, on some probability space, a sequence of random variables ![]() $X^n\sim\rho_n$ and
$X^n\sim\rho_n$ and ![]() $Y_j^n\sim\nu_j$, as well as
$Y_j^n\sim\nu_j$, as well as ![]() $X\sim\rho$ and
$X\sim\rho$ and ![]() $Y_j\sim\nu_j$, such that
$Y_j\sim\nu_j$, such that ![]() $X^n\to X$ and also, for each j,
$X^n\to X$ and also, for each j, ![]() $Y_j^n\to Y_j$ (convergence is a.s. and in
$Y_j^n\to Y_j$ (convergence is a.s. and in ![]() $L^2$). The sequence
$L^2$). The sequence ![]() $\{\mathbb E[Y_j^n\mid X^n]\colon n\in\mathbb N\}$ is
$\{\mathbb E[Y_j^n\mid X^n]\colon n\in\mathbb N\}$ is ![]() $L^2$-bounded, and hence by repeatedly applying Komlos’ theorem, we find yet another subsequence (relabeled so it is indexed by
$L^2$-bounded, and hence by repeatedly applying Komlos’ theorem, we find yet another subsequence (relabeled so it is indexed by ![]() $\mathbb N$) such that
$\mathbb N$) such that ![]() $({1}/{n})\sum_{r\leq n}\mathbb E[Y_j^r\mid X^r]\to Z_j$ almost surely and in
$({1}/{n})\sum_{r\leq n}\mathbb E[Y_j^r\mid X^r]\to Z_j$ almost surely and in ![]() $L^2$, for each j.
$L^2$, for each j.
We check that ![]() $\mathbb E[Z_j\mid X]=\mathbb E[Y_j\mid X] $. Indeed, if g is bounded and continuous,
$\mathbb E[Z_j\mid X]=\mathbb E[Y_j\mid X] $. Indeed, if g is bounded and continuous,
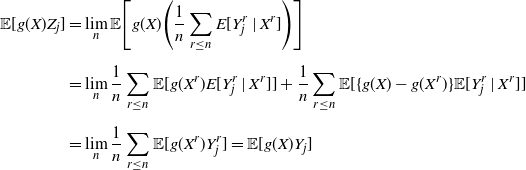 \begin{align*} \mathbb E[g(X)Z_j] & = \lim_n\mathbb E\Bigg[g(X)\Bigg(\frac{1}{n}\sum_{r\leq n}E[Y_j^r\mid X^r]\Bigg)\Bigg] \\[5pt] & = \lim_n\frac{1}{n}\sum_{r\leq n}\mathbb E[g(X^r)E[Y_j^r\mid X^r]] + \frac{1}{n}\sum_{r\leq n}\mathbb E[\{g(X)-g(X^r)\}\mathbb E[Y_j^r\mid X^r]] \\[5pt] & = \lim_n \frac{1}{n}\sum_{r\leq n}\mathbb E[g(X^r)Y_j^r] = \mathbb E[g(X)Y_j] \end{align*}
\begin{align*} \mathbb E[g(X)Z_j] & = \lim_n\mathbb E\Bigg[g(X)\Bigg(\frac{1}{n}\sum_{r\leq n}E[Y_j^r\mid X^r]\Bigg)\Bigg] \\[5pt] & = \lim_n\frac{1}{n}\sum_{r\leq n}\mathbb E[g(X^r)E[Y_j^r\mid X^r]] + \frac{1}{n}\sum_{r\leq n}\mathbb E[\{g(X)-g(X^r)\}\mathbb E[Y_j^r\mid X^r]] \\[5pt] & = \lim_n \frac{1}{n}\sum_{r\leq n}\mathbb E[g(X^r)Y_j^r] = \mathbb E[g(X)Y_j] \end{align*}
by dominated convergence. Also,
 \begin{align*} 0 & = \lim_n\|F'(\rho_n)\|_{L^2(\rho_n)}^2 \\[5pt] & = \lim_n\mathbb E\Bigg[\Bigg|X^n-\sum_{j=1}^\ell\lambda_j\mathbb E[Y_j^n\mid X^n]\Bigg|^2\Bigg] \\[5pt] & = \lim_n\frac{1}{n}\sum_{r\leq n} \mathbb E\Bigg[\Bigg|X^r-\sum_{j=1}^\ell\lambda_j\mathbb E[Y_j^r\mid X^r]\Bigg|^2\Bigg] \\[5pt] & \geq \lim_n\mathbb E\Bigg[\Bigg|\frac{1}{n}\sum_{r\leq n}X^r - \sum_{j=1}^\ell\lambda_j\frac{1}{n}\sum_{r\leq n}\mathbb E[Y_j^r\mid X^r]\Bigg|^2\Bigg] \\[5pt] & \geq \mathbb E\Bigg[\Bigg|X-\sum_{j=1}^\ell\lambda_j Z_j\Bigg|^2\Bigg] \geq \mathbb E\Bigg[\Bigg|X-\sum_{j=1}^\ell\lambda_j\mathbb E[Z_j\mid X]\Bigg|^2\Bigg], \end{align*}
\begin{align*} 0 & = \lim_n\|F'(\rho_n)\|_{L^2(\rho_n)}^2 \\[5pt] & = \lim_n\mathbb E\Bigg[\Bigg|X^n-\sum_{j=1}^\ell\lambda_j\mathbb E[Y_j^n\mid X^n]\Bigg|^2\Bigg] \\[5pt] & = \lim_n\frac{1}{n}\sum_{r\leq n} \mathbb E\Bigg[\Bigg|X^r-\sum_{j=1}^\ell\lambda_j\mathbb E[Y_j^r\mid X^r]\Bigg|^2\Bigg] \\[5pt] & \geq \lim_n\mathbb E\Bigg[\Bigg|\frac{1}{n}\sum_{r\leq n}X^r - \sum_{j=1}^\ell\lambda_j\frac{1}{n}\sum_{r\leq n}\mathbb E[Y_j^r\mid X^r]\Bigg|^2\Bigg] \\[5pt] & \geq \mathbb E\Bigg[\Bigg|X-\sum_{j=1}^\ell\lambda_j Z_j\Bigg|^2\Bigg] \geq \mathbb E\Bigg[\Bigg|X-\sum_{j=1}^\ell\lambda_j\mathbb E[Z_j\mid X]\Bigg|^2\Bigg], \end{align*}
and we conclude that ![]() $X=\sum_{j=1}^\ell\lambda_j\mathbb E[Y_j\mid X]$, almost surely. Finally, we remark that
$X=\sum_{j=1}^\ell\lambda_j\mathbb E[Y_j\mid X]$, almost surely. Finally, we remark that ![]() $\text{Law}(X,Y_j)\in\textsf{Opt}(\rho,\nu_j)$, and hence we conclude that
$\text{Law}(X,Y_j)\in\textsf{Opt}(\rho,\nu_j)$, and hence we conclude that ![]() $\rho$ is a Karcher mean.
$\rho$ is a Karcher mean.
We can now provide a convergence result. The hypotheses of this result are implied by the hypotheses of Theorem 1 in the case that ![]() $\Pi$ is concentrated on absolutely continuous measures. However, we stress that we do not know of any example where Theorem 5 is applicable and
$\Pi$ is concentrated on absolutely continuous measures. However, we stress that we do not know of any example where Theorem 5 is applicable and ![]() $\Pi$ is concentrated on non-absolutely continuous measures. For this reason we rather think that this result and its proof are a template of what could happen or could be done in the general case, and use it really to illustrate the difficulties present in the general case.
$\Pi$ is concentrated on non-absolutely continuous measures. For this reason we rather think that this result and its proof are a template of what could happen or could be done in the general case, and use it really to illustrate the difficulties present in the general case.
Theorem 5. Assume Assumptions 1 and 2′′, conditions (3) and (4), that ![]() $\Pi$ admits a unique Karcher mean (in the sense of Definition 8) in
$\Pi$ admits a unique Karcher mean (in the sense of Definition 8) in ![]() $K_\Pi$, and that
$K_\Pi$, and that ![]() $K_\Pi$ contains a (hence, exactly one) 2-Wasserstein barycenter
$K_\Pi$ contains a (hence, exactly one) 2-Wasserstein barycenter ![]() $\hat\mu$. Then, the SGD sequence
$\hat\mu$. Then, the SGD sequence ![]() $\{\mu_k\}_k$ in (26) is almost surely convergent to
$\{\mu_k\}_k$ in (26) is almost surely convergent to ![]() $\hat{\mu}$.
$\hat{\mu}$.
Proof. The proof of Theorem 1 can be followed verbatim up to (15), namely that ![]() $\liminf_{t\to\infty}\|F^\prime(\mu_t)\|^2_{L^2(\mu_t)}=0$ almost surely.
$\liminf_{t\to\infty}\|F^\prime(\mu_t)\|^2_{L^2(\mu_t)}=0$ almost surely.
We observe that if ![]() $\rho_n\to\rho$ with
$\rho_n\to\rho$ with ![]() $\{\rho_n\}_n\subset K_\Pi$ is such that
$\{\rho_n\}_n\subset K_\Pi$ is such that ![]() $F(\rho_n)\geq F(\hat\mu)+\varepsilon$, for
$F(\rho_n)\geq F(\hat\mu)+\varepsilon$, for ![]() $\varepsilon>0$, and
$\varepsilon>0$, and ![]() $\|F^\prime(\rho_n)\|^2_{L^2(\rho_n)}\to 0$, then by Lemma 6
$\|F^\prime(\rho_n)\|^2_{L^2(\rho_n)}\to 0$, then by Lemma 6 ![]() $\rho$ is a Karcher mean in
$\rho$ is a Karcher mean in ![]() $K_\Pi$ that is necessarily different from
$K_\Pi$ that is necessarily different from ![]() $\hat\mu$. This would contradict the uniqueness of Karcher means in
$\hat\mu$. This would contradict the uniqueness of Karcher means in ![]() $K_\Pi$. Thus we establish that, for all
$K_\Pi$. Thus we establish that, for all ![]() $\varepsilon>0$,
$\varepsilon>0$, ![]() $\inf_{\{\rho:F(\rho)\geq\hat F+\varepsilon\}\cap K_\Pi}\|F^\prime(\rho)\|^2_{L^2(\rho)}>0$. From here on we can again follow the proof of Theorem 1.
$\inf_{\{\rho:F(\rho)\geq\hat F+\varepsilon\}\cap K_\Pi}\|F^\prime(\rho)\|^2_{L^2(\rho)}>0$. From here on we can again follow the proof of Theorem 1.
In the absolutely continuous case covered in the rest of this paper, we required the Karcher mean to be absolutely continuous. Moreover, in this case there is a unique barycenter (automatically absolutely continuous). Once we leave the absolutely continuous world we have to be more careful, as illustrated by the following example.
Example 2. Let Z be an ![]() $\mathcal X$-valued random variable with finite second moment, and let
$\mathcal X$-valued random variable with finite second moment, and let ![]() $b_j\in\mathcal X$ with
$b_j\in\mathcal X$ with ![]() $\sum_j\lambda_j b_j=0$. Define
$\sum_j\lambda_j b_j=0$. Define ![]() $\nu_j\;:\!=\;\mathrm{Law}(Z+b_j)$. Then
$\nu_j\;:\!=\;\mathrm{Law}(Z+b_j)$. Then ![]() $X\sim\mu$ is a Karcher mean if and ony if
$X\sim\mu$ is a Karcher mean if and ony if ![]() $X=\mathbb E[Z\mid X]$ for some optimal coupling of X and Z. Hence,
$X=\mathbb E[Z\mid X]$ for some optimal coupling of X and Z. Hence, ![]() $X\;:\!=\;Z$ and
$X\;:\!=\;Z$ and ![]() $X\;:\!=\;\mathbb E[Z]$ are both Karcher means per Definition 8, even if Z (and so each
$X\;:\!=\;\mathbb E[Z]$ are both Karcher means per Definition 8, even if Z (and so each ![]() $\nu_j$) is absolutely continuous. On the other hand, we can check that the barycenter of the
$\nu_j$) is absolutely continuous. On the other hand, we can check that the barycenter of the ![]() $\nu_j$ is unique and given by
$\nu_j$ is unique and given by ![]() $\mathrm{Law}(Z)$.
$\mathrm{Law}(Z)$.
Example 3. We continue in the setting of the previous example and choose ![]() $\mathcal X=\mathbb R^2$. Here,
$\mathcal X=\mathbb R^2$. Here, ![]() $Z=(B,0)$ with
$Z=(B,0)$ with ![]() $B\in\{-1,1\}$ with equal probabilities, and
$B\in\{-1,1\}$ with equal probabilities, and ![]() $\nu_1=\mathrm{Law}((B,1))$,
$\nu_1=\mathrm{Law}((B,1))$, ![]() $\nu_2=\mathrm{Law}((B,-1))$. In this case we check that
$\nu_2=\mathrm{Law}((B,-1))$. In this case we check that ![]() $\mu^p\;:\!=\;p(\delta_{(1,0)}+\delta_{(\!-\!1,0)})+(1-2p)\delta_{(0,0)}$ is a Karcher mean for each
$\mu^p\;:\!=\;p(\delta_{(1,0)}+\delta_{(\!-\!1,0)})+(1-2p)\delta_{(0,0)}$ is a Karcher mean for each ![]() $p\in\big[0,\frac12\big]$. In particular, the barycenter, given by
$p\in\big[0,\frac12\big]$. In particular, the barycenter, given by ![]() $\mu^1$, is not isolated in the sense that any ball around
$\mu^1$, is not isolated in the sense that any ball around ![]() $\mu^1$ contains other Karcher means (taking p close to 0.5), and moreover those Karcher means might be more ‘regular’ than the barycenter in the sense of having a strictly larger support. Also note that if we define
$\mu^1$ contains other Karcher means (taking p close to 0.5), and moreover those Karcher means might be more ‘regular’ than the barycenter in the sense of having a strictly larger support. Also note that if we define ![]() $K\;:\!=\;\{\mathrm{Law}((B,r))\colon r\in I\}$ with I some interval containing
$K\;:\!=\;\{\mathrm{Law}((B,r))\colon r\in I\}$ with I some interval containing ![]() $\pm 1$, then K is compact, contains the
$\pm 1$, then K is compact, contains the ![]() $\nu_i$, and transport maps between elements in K are associative.
$\nu_i$, and transport maps between elements in K are associative.
Examples 2 and 3 show that uniqueness of Karcher means (in the sense of Definition 8), or even their uniqueness within a nice set ![]() $K_\Pi$, is an assumption that is difficult to verify in the general case. Furthermore, we encounter the same problem with a localized version of this assumption (for example: ‘uniqueness of Karcher means in a small ball intersected with
$K_\Pi$, is an assumption that is difficult to verify in the general case. Furthermore, we encounter the same problem with a localized version of this assumption (for example: ‘uniqueness of Karcher means in a small ball intersected with ![]() $K_\Pi$’). To complicate the matter further, it is known that in the general case multiple barycenters may exist. For all these reasons we are inclined to believe that the correct object of study in the general case is the regularized barycenter problem (or, more ambitiously, the limit of such regularized problems as the regularization parameter goes to zero at a suitable speed). We refer the reader to [Reference Chizat20, Reference Chizat and Vaškevic̆ius22], and the references therein, for promising results in this direction.
$K_\Pi$’). To complicate the matter further, it is known that in the general case multiple barycenters may exist. For all these reasons we are inclined to believe that the correct object of study in the general case is the regularized barycenter problem (or, more ambitiously, the limit of such regularized problems as the regularization parameter goes to zero at a suitable speed). We refer the reader to [Reference Chizat20, Reference Chizat and Vaškevic̆ius22], and the references therein, for promising results in this direction.
Acknowledgements
We thank two anonymous referees for their valuable comments and questions that motivated some improvements of our results and of the presentation of the paper.
Funding information
This research was funded in whole or in part by the by the Austrian Science Fund (FWF) DOI 10.55776/P36835 (JB) and the ANID-Chile grants Fondecyt-Regular 1201948 (JF) and 1210606 (FT); Center for Mathematical Modeling ACE210010 and FB210005 (JF, FT); and Advanced Center for Electrical and Electronic Engineering FB0008 (FT).
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.



