Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-05T16:51:29.980Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic comparisons of order statistics under multivariate imperfect repair

Part of: Survival analysis and censored data Nonparametric inference

Published online by Cambridge University Press:  14 July 2016

Taizhong Hu
Taizhong Hu*
Affiliation:
University of Science and Technology of China
*
∗Postal address: Department of Mathematics, University of Science and Technology of China, Hefei, Anhui 230026, People's Republic of China.
Get access Rights & Permissions [Opens in a new window]

Abstract

A monotone coupling of order statistics from two sets of independent non-negative random variables Xi, i = 1, ···, n, and Yi, i = 1, ···, n, means that there exist random variables X′i, Y′i, i = 1, ···, n, on a common probability space such that 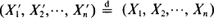, 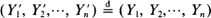and 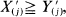a.s. j = 1, ···, n, where X(1) ≦ X(2) ≦ ·· ·≦ X(n) are the order statistics of Xi, i = 1, ···, n (with the corresponding notations for the X′, Y, Y′ sample). In this paper, we study the monotone coupling of order statistics of lifetimes in two multi-unit systems under multivariate imperfect repair. Similar results for a special model due to Ross are also given.

Keywords

MONOTONE COUPLINGORDER STATISTICSSTOCHASTIC ORDERINGMULTIVARIATE IMPERFECT REPAIR

MSC classification

Primary: 62N05: Reliability and life testing
Secondary: 62G30: Order statistics; empirical distribution functions
Type
Research Papers
Information
Journal of Applied Probability , Volume 33 , Issue 1 , March 1996 , pp. 156 - 163
Copyright
Copyright © Applied Probability Trust 1996 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by a NNSF of China and a grant of Chinese Academy of Sciences.

References

Ball, F. (1985) Deterministic and stochastic epidemic with several kinds of susceptibles. Adv. Appl. Prob. 17, 1–22.CrossRefGoogle Scholar
Barbour, A. D., Lindvall, T. and Rogers, L. C. G. (1991) Stochastic ordering of order statistics. J. Appl. Prob. 28, 278–286.Google Scholar
Hu, T. Z. (1995) Monotone coupling and stochastic ordering of order statistics. Sys. Sci. Math. Sci. 8, 209–214.Google Scholar
Karlin, S. and Rinott, Y. (1980) Classes of ordering of measures and related correlation inequalities. I. Multivariate totally positive distributions. J. Multi. Anal. 10, 241–258.Google Scholar
Marshall, A. W. and Olkin, I. (1979) Inequalities: Theory of Majorization and its Applications. Academic Press, New York.Google Scholar
Proschan, F. and Sethuraman, J. (1976) Stochastic comparison of order statistics from heterogenous populations with applications in reliability. J. Multi. Anal. 6, 608–616.Google Scholar
Ross, S. M. (1984) A model in which component failure rates depend on the working set. Naval Res. Log. Quart. 31, 297–301.Google Scholar
Shaked, M. and Shanthikumar, J. G. (1986) Multivariate imperfect repair. Operat. Res. 34, 437–448.Google Scholar
Shaked, M. and Shanthikumar, J. G. (1987a) The multivariate hazard construction. Stoch. Proc. Appl. 24, 241–258.Google Scholar
Shaked, M. and Shanthikumar, J. G. (1987b) Multivariate hazard rates and stochastic ordering. Adv. Appl. Prob. 19, 123–137.Google Scholar