Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T05:42:07.118Z Has data issue: false hasContentIssue false
  • English
  • Français

Steady-state analysis of load-balancing algorithms in the sub-Halfin–Whitt regime

Part of: Operations research and management science Computer system organization Special processes

Published online by Cambridge University Press:  16 July 2020

Xin Liu  and
Lei Ying
Xin Liu*
Affiliation:
Arizona State University
Lei Ying*
Affiliation:
Arizona State University
*
*Postal address: School of Electrical, Computer and Energy Engineering, 436 Goldwater Center for Science and Engineering, 650 E Tyler Mall, Arizona State University, Tempe, AZ 85287, USA.
*Postal address: School of Electrical, Computer and Energy Engineering, 436 Goldwater Center for Science and Engineering, 650 E Tyler Mall, Arizona State University, Tempe, AZ 85287, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

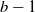We study a class of load-balancing algorithms for many-server systems (N servers). Each server has a buffer of size $b-1$ with 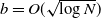$b=O(\sqrt{\log N})$, i.e. a server can have at most one job in service and 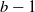$b-1$ jobs queued. We focus on the steady-state performance of load-balancing algorithms in the heavy traffic regime such that the load of the system is 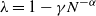$\lambda = 1 - \gamma N^{-\alpha}$ for 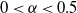$0<\alpha<0.5$ and 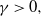$\gamma > 0,$ which we call the sub-Halfin–Whitt regime (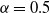$\alpha=0.5$ is the so-called Halfin–Whitt regime). We establish a sufficient condition under which the probability that an incoming job is routed to an idle server is 1 asymptotically (as 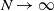$N \to \infty$) at steady state. The class of load-balancing algorithms that satisfy the condition includes join-the-shortest-queue, idle-one-first, join-the-idle-queue, and power-of-d-choices with 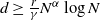$d\geq \frac{r}{\gamma}N^\alpha\log N$ (r a positive integer). The proof of the main result is based on the framework of Stein’s method. A key contribution is to use a simple generator approximation based on state space collapse.

Keywords

Many-server systemsload balancingheavy trafficStein’s methodmean-field modelsteady statestate space collapseasymptotic zero delay

MSC classification

Primary: 90B15: Network models, stochastic
Secondary: 60K25: Queueing theory 68M20: Performance evaluation; queueing; scheduling
Type
Research Papers
Information
Journal of Applied Probability , Volume 57 , Issue 2 , June 2020 , pp. 578 - 596
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Banerjee, S. and Mukherjee, D. (2018). Join-the-shortest queue diffusion limit in Halfin–Whitt regime: Tail asymptotics and scaling of extrema. arXiv:1803.03306.Google Scholar
Bertsimas, D., Gamarnik, D. and Tsitsiklis, J. N. (2001). Performance of multiclass Markovian queueing networks via piecewise linear Lyapunov functions. Ann. Appl. Prob. 11, 1384–1428.CrossRefGoogle Scholar
Braverman, A. (2018). Steady-state analysis of the join the shortest queue model in the Halfin–Whitt regime. arXiv:1801.05121.Google Scholar
Braverman, A. and Dai, J. G. (2017). Stein’s method for steady-state diffusion approximations of $m/\mathit{Ph}/n+m$ systems. Ann. Appl. Prob. 27, 550–581.10.1214/16-AAP1211CrossRefGoogle Scholar
Braverman, A., Dai, J. G. and Feng, J. (2016). Stein’s method for steady-state diffusion approximations: An introduction through the Erlang-A and Erlang-C models. Stoch. Syst. 6, 301–366.10.1287/15-SSY212CrossRefGoogle Scholar
Eschenfeldt, P. and Gamarnik, D. (2018). Join the shortest queue with many servers. The heavy-traffic asymptotics. Math. Operat. Res. 43, 867–886.Google Scholar
Gast, N. (2017). Expected values estimated via mean-field approximation are $1/n$-accurate. Proc. ACM Meas. Anal. Comput. Syst. 1, 17:1–17:26.Google Scholar
Gast, N. and Van Houdt, B. (2018). A refined mean field approximation. In Proc. Ann. ACM SIGMETRICS Conf., Irvine, CA.10.1145/3219617.3219663CrossRefGoogle Scholar
Gupta, V. and Walton, N. (2017). Load balancing in the non-degenerate slowdown regime. arXiv:1707.01969.Google Scholar
Liu, X. and Ying, L. (2018). On achieving zero delay with power-of-d-choices load balancing. In Proc. IEEE Int. Conf. Computer Communications (INFOCOM), Honolulu, Hawaii.10.1109/INFOCOM.2018.8485827CrossRefGoogle Scholar
Lu, Y., Xie, Q., Kliot, G., Geller, A., Larus, J. R. and Greenberg, A. (2011). Join-Idle-Queue: A novel load balancing algorithm for dynamically scalable web services. Performance Evaluation 68, 1056–1071.10.1016/j.peva.2011.07.015CrossRefGoogle Scholar
Mitzenmacher, M. (1996). The power of two choices in randomized load balancing. Ph.D. thesis, University of California at Berkeley.Google Scholar
Mukherjee, D., Borst, S. C., van Leeuwaarden, J. S. and Whiting, P. A. (2016). Universality of power-of-d load balancing in many-server systems. arXiv:1612.00723.Google Scholar
Stolyar, A. (2015). Pull-based load distribution in large-scale heterogeneous service systems. Queueing Syst. 80, 341–361.CrossRefGoogle Scholar
Stolyar, A. (2015). Tightness of stationary distributions of a flexible-server system in the Halfin–Whitt asymptotic regime. Stoch. Syst. 5, 239–267.10.1287/14-SSY139CrossRefGoogle Scholar
van der Boor, M., Borst, S. C., van Leeuwaarden, J. S. and Mukherjee, D. (2017). Scalable load balancing in networked systems: Universality properties and stochastic coupling methods. arXiv:1712.08555.Google Scholar
Vvedenskaya, N. D., Dobrushin, R. L. and Karpelevich, F. I. (1996). Queueing system with selection of the shortest of two queues: An asymptotic approach. Problemy Peredachi Informatsii 32, 20–34.Google Scholar
Wang, W., Maguluri, S. T., Srikant, R. and Ying, L. (2017). Heavy-traffic delay insensitivity in connection-level models of data transfer with proportionally fair bandwidth sharing. ACM SIGMETRICS Performance 45, 232–245.10.1145/3199524.3199565CrossRefGoogle Scholar
Weber, R. R. (1978). On the optimal assignment of customers to parallel servers. J. Appl. Prob. 15, 406–413.10.2307/3213411CrossRefGoogle Scholar
Winston, W. (1977). Optimality of the shortest line discipline. J. Appl. Prob. 14, 181–189.10.2307/3213271CrossRefGoogle Scholar
Ying, L. (2016). On the approximation error of mean-field models. In Proc. Ann. ACM SIGMETRICS Conf., Antibes Juan-les-Pins, France, pp. 285–297.10.1145/2964791.2901463CrossRefGoogle Scholar
Ying, L. (2017). Stein’s method for mean field approximations in light and heavy traffic regimes. Proc. ACM Meas. Anal. Comput. Syst. 1, 12:1–12:27.Google Scholar