If the step-length distribution function F for a random walk {Sn, n ≧ 0} is either continuous and symmetric or belongs to the domain of attraction of a symmetric stable law, then it is clear that the symmetric form of ‘Spitzer's condition' holds, i.e. 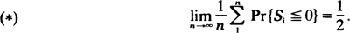The question considered in this note is whether or not (⋆) can hold for other random walks. The answer is in the affirmative, for we show that (⋆) holds for a large class of random walks for which F is neither symmetric nor belongs to any domain of attraction; all such random walks are asymptotically symmetric, in the sense that limx→∞ {F(–x)| 1 – F(x)} = 1, but we show by an example that this is not a sufficient condition for (⋆) to hold.