Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T17:51:00.860Z Has data issue: false hasContentIssue false
  • English
  • Français

Some exact distributions of a last one-sided exit time in the simple random walk

Published online by Cambridge University Press:  14 July 2016

Chern-Ching Chao  and
John Slivka
Chern-Ching Chao
Affiliation:
State University of New York at Buffalo
John Slivka*
Affiliation:
State University of New York at Buffalo
*
∗∗Postal address: Department of Mathematics, State University College, 1300 Elmwood Avenue, Buffalo, NY 14222, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

For each positive integer n, let Sn be the nth partial sum of a sequence of i.i.d. random variables which assume the values +1 and −1 with respective probabilities p and 1 – p, having mean μ= 2p − 1. The exact distribution of the random variable 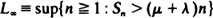, where sup Ø= 0, is given for the case that λ > 0 and μ+ λ= k/(k + 2) for any non-negative integer k. Tables to the 99.99 percentile of some of these distributions, as well as a limiting distribution, are given for the special case of a symmetric simple random walk (p = 1/2).

Keywords

STRONG LAW OF LARGE NUMBERSSUMS OF I.I.D. BERNOULLI VARIABLESLINEAR BOUNDARY CROSSINGSLAST DEVIATION
Type
Research Paper
Information
Journal of Applied Probability , Volume 23 , Issue 2 , June 1986 , pp. 332 - 340
Copyright
Copyright © Applied Probability Trust 1986 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

∗

Present address: Department of Statistics, University of Kentucky, Lexington, KY 40506, USA.

This investigation was partially supported by a Research Development Fund Award from the State University of New York Research Foundation.

References

[1] Chow, Y. S. and Lai, T. L. (1975) Some one-sided theorems on the tail distribution of sample sums with applications to the last time and largest excess of boundary crossings. Trans. Amer. Math. Soc. 208, 51–72.CrossRefGoogle Scholar
[2] Feller, W. (1968) An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. Wiley, New York.Google Scholar
[3] Griffiths, G. N. and Wright, F. T. (1975) Moments of the number of deviations of sums of independent identically distributed random variables. Sankhya A 37, 452–455.Google Scholar
[4] Kao, C. (1978) On the time and the excess of linear boundary crossings of sample sums. Ann. Statist. 6, 191–199.Google Scholar
[5] Lai, T. L. (1976) On r-quick convergence and a conjecture of Strassen. Ann. Prob. 4, 612–627.Google Scholar
[6] Lai, T. L. and Lan, K. K. (1976) On the last time and the number of boundary crossings related to the strong law of large numbers and the law of the iterated logarithm. Z. Wahrscheinlichkeitsth. 34, 59–71.Google Scholar
[7] Robbins, H., Siegmund, D. and Wendel, J. (1968) The limiting distribution of the last time sn ≧ ne . Proc. Nat. Acad. Sci. USA 61, 1228–1230.Google Scholar
[8] Slivka, J. (1970) Some density functions of a counting variable in the simple random walk. Skand. Aktuarietidskr. 53, 51–57.Google Scholar
[9] Slivka, J. and Severo, N. C. (1970) On the strong law of large numbers. Proc. Amer. Math. Soc. 24, 729–734.Google Scholar
[10] Strassen, V. (1967) Almost sure behavior of sums of independent random variables and martingales. Proc. 5th Berkeley Symp. Math. Statist. Prob. 2, 315–343.Google Scholar
[11] Stratton, H. H. (1972) Moments of oscillations and ruled sums. Ann. Math. Statist. 43, 1012–1016.CrossRefGoogle Scholar