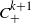1. Introduction and results
Reconstructing a possibly unknown set, or some of its characteristic quantities, from a random sample of points is a much-investigated classical problem that arises naturally in various fields, like stereology [Reference Baddeley and Vedel Jensen1], computational geometry [Reference Goodman, O’Rourke and Tóth13], statistical quality control [Reference Devroye and Wise8], etc. Estimating the shape, volume, surface area, and other characteristic quantities of sets is of interest both in geometry and statistics, although the aspects investigated are in many cases different in the respective fields. For an overview of set estimation see, for example, [Reference Cuevas and Rodrguez-Casal7]. The set may be quite arbitrary, but often various restrictions are imposed on it. One common such restriction that has received much attention is when the set is required to be convex. In such a setting polytopes spanned by random samples of points from the set form a natural estimator. The theory of random polytopes is a rich and lively field with numerous applications. For a recent review and further references see, for example, [Reference Schneider31]. The convex hull is an optimal estimator if no further restrictions are imposed on the set K other than convexity. However, in this paper we study another estimator under further assumptions on K, namely that the degree of smoothness of the boundary of K is prescribed to be
![]() $C^{k+1}$
, and it also assumed that the curvature is positive everywhere. Under these circumstances, using congruent circles to form the hull of the sample yields better performance than the classical convex hull.
$C^{k+1}$
, and it also assumed that the curvature is positive everywhere. Under these circumstances, using congruent circles to form the hull of the sample yields better performance than the classical convex hull.
Since the case when the number of random points is fixed is notoriously difficult, it has become common to investigate the asymptotic behaviour of functionals associated with random polytopes as the number of points in the sample tends to infinity. The investigations of the asymptotic behaviour of random polytopes started with the classical papers [Reference Rényi and Sulanke26, Reference Rényi and Sulanke27] in the 1960s. They studied the following particular model in the plane. Let K be a convex body (a compact convex set with nonempty interior) in d-dimensional Euclidean space
![]() $\mathbb{R}^d$
, and let
$\mathbb{R}^d$
, and let
![]() $x_1, \ldots, x_n$
be independent random points from K selected according to the uniform probability distribution.
$x_1, \ldots, x_n$
be independent random points from K selected according to the uniform probability distribution.
The convex hull
![]() $K_n=[x_1,\ldots, x_n]$
of
$K_n=[x_1,\ldots, x_n]$
of
![]() $x_1, \ldots , x_n$
is called a (uniform) random polytope in K. Asymptotic formulas in the plane were proved in [Reference Rényi and Sulanke26, Reference Rényi and Sulanke27] for the expected number
$x_1, \ldots , x_n$
is called a (uniform) random polytope in K. Asymptotic formulas in the plane were proved in [Reference Rényi and Sulanke26, Reference Rényi and Sulanke27] for the expected number
![]() $f_0(K_n)$
of vertices of
$f_0(K_n)$
of vertices of
![]() $K_n$
and the expectation of the missed area
$K_n$
and the expectation of the missed area
![]() $A(K\setminus K_n)$
under the assumption that the boundary
$A(K\setminus K_n)$
under the assumption that the boundary
![]() $\partial K$
of K is sufficiently smooth, and also in the case when K itself is a convex polygon. This was extended in [Reference Wieacker35] to the d-dimensional ball
$\partial K$
of K is sufficiently smooth, and also in the case when K itself is a convex polygon. This was extended in [Reference Wieacker35] to the d-dimensional ball
![]() $B^d$
, and in [Reference Bárány2] for d-dimensional convex bodies with at least a
$B^d$
, and in [Reference Bárány2] for d-dimensional convex bodies with at least a
![]() $C^3_+$
-smooth boundary (three times continuously differentiable with everywhere positive Gauss–Kronecker curvature). All smoothness conditions were removed in [Reference Schütt33]. The results were extended in [Reference Böröczky, Fodor and Hug6] for nonuniform distributions and weighted volume difference.
$C^3_+$
-smooth boundary (three times continuously differentiable with everywhere positive Gauss–Kronecker curvature). All smoothness conditions were removed in [Reference Schütt33]. The results were extended in [Reference Böröczky, Fodor and Hug6] for nonuniform distributions and weighted volume difference.
Let
![]() $V_i(\!\cdot\!)$
,
$V_i(\!\cdot\!)$
,
![]() $i=1,\ldots , d$
, denote the ith intrinsic volume of a convex body. A power series expansion of the quantity
$i=1,\ldots , d$
, denote the ith intrinsic volume of a convex body. A power series expansion of the quantity
![]() $\mathbb{E}(V_i(K)-V_i(K_n))$
for all
$\mathbb{E}(V_i(K)-V_i(K_n))$
for all
![]() $i=1,\ldots, d$
as
$i=1,\ldots, d$
as
![]() $n\to\infty$
was established in [Reference Reitzner24] under stronger smoothness conditions on the boundary of K.
$n\to\infty$
was established in [Reference Reitzner24] under stronger smoothness conditions on the boundary of K.
Theorem 1. ([Reference Reitzner24].) Let K be a convex body in
![]() $\mathbb{R}^d$
with
$\mathbb{R}^d$
with
![]() $V_d(K)=1$
whose boundary
$V_d(K)=1$
whose boundary
![]() $\partial K$
is
$\partial K$
is
![]() $C^{k+1}_+$
for some integer
$C^{k+1}_+$
for some integer
![]() $k\geq 2$
. Then
$k\geq 2$
. Then
 \begin{align} & \mathbb{E}(V_i(K)-V_i(K_n)) \nonumber \\[5pt] & = c_2^{(i,d)}(K)n^{-{2}/({d+1})} + c_3^{(i,d)}(K)n^{-{3}/({d+1})} + \cdots + c_{k}^{(i,d)}(K)n^{-{k}/({d+1})} + O(n^{-({k+1})/({d+1})}) \end{align}
\begin{align} & \mathbb{E}(V_i(K)-V_i(K_n)) \nonumber \\[5pt] & = c_2^{(i,d)}(K)n^{-{2}/({d+1})} + c_3^{(i,d)}(K)n^{-{3}/({d+1})} + \cdots + c_{k}^{(i,d)}(K)n^{-{k}/({d+1})} + O(n^{-({k+1})/({d+1})}) \end{align}
as
![]() $n\to\infty$
. Moreover,
$n\to\infty$
. Moreover,
![]() $c_{2m+1}^{(i,d)}=0$
for all
$c_{2m+1}^{(i,d)}=0$
for all
![]() $m\leq d/2$
if d is even, and
$m\leq d/2$
if d is even, and
![]() $c_{2m+1}^{(i,d)}=0$
for all m if d is odd.
$c_{2m+1}^{(i,d)}=0$
for all m if d is odd.
Under the same conditions as in Theorem 1, we can obtain from (1) a series expansion for the number of vertices
![]() $\mathbb{E}(f_0(K_n))$
via Efron’s identity [Reference Efron10]:
$\mathbb{E}(f_0(K_n))$
via Efron’s identity [Reference Efron10]:
 \begin{align*} & \mathbb{E}(f_0(K_n)) \\[5pt] & = d_2(K)n^{({d-1})/({d+1})} + d_3(K)n^{({d-2})/({d+1})} + \cdots + d_{k}(K)n^{({d-k+1})/({d+1})} + O(n^{({d-k+2})/({d+1})})\end{align*}
\begin{align*} & \mathbb{E}(f_0(K_n)) \\[5pt] & = d_2(K)n^{({d-1})/({d+1})} + d_3(K)n^{({d-2})/({d+1})} + \cdots + d_{k}(K)n^{({d-k+1})/({d+1})} + O(n^{({d-k+2})/({d+1})})\end{align*}
as
![]() $n\to\infty$
, where the coefficients
$n\to\infty$
, where the coefficients
![]() $d_i(K)$
also depend on the dimension d.
$d_i(K)$
also depend on the dimension d.
Theorem 1 was proved in [Reference Gruber14] when
![]() $i=1$
. Using properties of the convex floating body, the planar case of Theorem 1 was established for the area (
$i=1$
. Using properties of the convex floating body, the planar case of Theorem 1 was established for the area (
![]() $d=2$
,
$d=2$
,
![]() $i=2$
) in [Reference Reitzner23]. In particular, it was proved that
$i=2$
) in [Reference Reitzner23]. In particular, it was proved that
where
![]() $\Gamma(\!\cdot\!)$
is Euler’s gamma function, k(x) is the affine curvature (for information about the affine curvature see, for example, [Reference Blaschke5, pp. 12–15] or [Reference Guggenheimer15, Section 7.3]),
$\Gamma(\!\cdot\!)$
is Euler’s gamma function, k(x) is the affine curvature (for information about the affine curvature see, for example, [Reference Blaschke5, pp. 12–15] or [Reference Guggenheimer15, Section 7.3]),
![]() $\kappa(x)$
is the curvature of
$\kappa(x)$
is the curvature of
![]() $\partial K$
at x, and integration on the boundary
$\partial K$
at x, and integration on the boundary
![]() $\partial K$
of K is with respect to arc length.
$\partial K$
of K is with respect to arc length.
For more information about approximations of convex bodies by classical random polytopes we refer to [Reference Bárány3, Reference Reitzner25, Reference Schneider31, Reference Schneider and Weil32, Reference Weil, Wieacker and Part34].
When estimating a planar convex body under curvature restrictions, it may naturally be more advantageous to use suitably curved arcs to form the boundary of the approximating set that fit K better than line segments. One of the simplest such constructions uses radius-R circular arcs and the resulting (convex) hull is called, among other names, the R-spindle convex hull; for precise definitions, see below. The radius should be chosen in such a way that the (generalised) random polygon is still contained in K. This imposes the condition on R that it should be at least as large as the maximum radius of curvature of
![]() $\partial K$
. However, similarly to the classical convex case, difficulties arise when R is equal to the maximal radius of curvature, so this case usually needs separate treatment using different methods.
$\partial K$
. However, similarly to the classical convex case, difficulties arise when R is equal to the maximal radius of curvature, so this case usually needs separate treatment using different methods.
In this paper, we study the R-spindle convex variant of the above probability model in the Euclidean plane
![]() $\mathbb{R}^2$
. Let
$\mathbb{R}^2$
. Let
![]() $R>0$
be fixed, and let
$R>0$
be fixed, and let
![]() $x,y\in\mathbb{R}^2$
be such that their distance is at most 2R. We call the intersection
$x,y\in\mathbb{R}^2$
be such that their distance is at most 2R. We call the intersection
![]() $[x,y]_R$
of all (closed circular) discs of radius R that contain both x and y the R-spindle of x and y. A set
$[x,y]_R$
of all (closed circular) discs of radius R that contain both x and y the R-spindle of x and y. A set
![]() $X\subseteq \mathbb{R}^2$
is called R-spindle convex if from
$X\subseteq \mathbb{R}^2$
is called R-spindle convex if from
![]() $x,y\in X$
it follows that
$x,y\in X$
it follows that
![]() $[x,y]_R\subseteq X$
. Spindle convex sets are also convex in the usual linear sense. In this paper we restrict our attention to compact spindle-convex sets. One can show (cf. [Reference Bezdek, Lángi, Naszódi and Papez4, Corollary 3.4, p. 205]) that a convex body in
$[x,y]_R\subseteq X$
. Spindle convex sets are also convex in the usual linear sense. In this paper we restrict our attention to compact spindle-convex sets. One can show (cf. [Reference Bezdek, Lángi, Naszódi and Papez4, Corollary 3.4, p. 205]) that a convex body in
![]() $\mathbb{R}^2$
is R-spindle convex if it is the intersection of (not necessarily finitely many) closed discs of radius R. The intersection of finitely many closed discs of radius R is called a convex R-disc-polygon. Let X be a compact set which is contained in a closed disc of radius R. The intersection of all planar R-spindle-convex bodies containing X is called the R-spindle-convex hull of X, and it is denoted by
$\mathbb{R}^2$
is R-spindle convex if it is the intersection of (not necessarily finitely many) closed discs of radius R. The intersection of finitely many closed discs of radius R is called a convex R-disc-polygon. Let X be a compact set which is contained in a closed disc of radius R. The intersection of all planar R-spindle-convex bodies containing X is called the R-spindle-convex hull of X, and it is denoted by
![]() $[X]_R$
. Perhaps it is easier to grasp this notion if we point out the similarity with the classical convex hull. In the R-spindle-convex case the radius-R discs play a similar role to what closed half-spaces do for classical convex hulls. Thus, in a heuristic way, we can consider the classical convex hull as a limiting case as
$[X]_R$
. Perhaps it is easier to grasp this notion if we point out the similarity with the classical convex hull. In the R-spindle-convex case the radius-R discs play a similar role to what closed half-spaces do for classical convex hulls. Thus, in a heuristic way, we can consider the classical convex hull as a limiting case as
![]() $R\to\infty$
. If
$R\to\infty$
. If
![]() $X\subset K$
for an R-spindle-convex body K in
$X\subset K$
for an R-spindle-convex body K in
![]() $\mathbb{R}^2$
, then
$\mathbb{R}^2$
, then
![]() $[X]_R\subset K$
. A prominent class of R-spindle-convex sets in
$[X]_R\subset K$
. A prominent class of R-spindle-convex sets in
![]() $\mathbb{R}^2$
that are directly relevant in this paper is provided by convex bodies whose boundary is
$\mathbb{R}^2$
that are directly relevant in this paper is provided by convex bodies whose boundary is
![]() $C^2_+$
-smooth with curvature
$C^2_+$
-smooth with curvature
![]() $\kappa(x)\geq 1/R$
for all boundary points
$\kappa(x)\geq 1/R$
for all boundary points
![]() $x\in\partial K$
[Reference Schneider30, Sections 2.5 and 3.2]. For more detailed information about spindle convexity we refer to [Reference Bezdek, Lángi, Naszódi and Papez4, Reference Martini, Montejano and Oliveros19].
$x\in\partial K$
[Reference Schneider30, Sections 2.5 and 3.2]. For more detailed information about spindle convexity we refer to [Reference Bezdek, Lángi, Naszódi and Papez4, Reference Martini, Montejano and Oliveros19].
We note that there exist further generalisations of spindle convexity, most notably the concept of L-convexity in which the translates of a fixed convex body L play the role of the radius-R closed disc; for more information, see, for example, [Reference Lángi, Naszódi and Talata17]. Another further generalisation is H-convexity as introduced in [Reference Kabluchko, Marynych and Molchanov16], where the hull of a set is generated by intersections of transformed copies of a fixed convex set C by a set H of affine transformations. A similar concept (see, for example, [Reference Mani-Levitska18]) to R-spindle convexity, called
![]() $\alpha$
convexity, also exists, where the
$\alpha$
convexity, also exists, where the
![]() $\alpha$
-convex hull of a set is defined as the complement of the union of all radius-r open balls disjoint from the set. The
$\alpha$
-convex hull of a set is defined as the complement of the union of all radius-r open balls disjoint from the set. The
![]() $\alpha$
-convex hull of a finite sample is different from its R-spindle-convex hull as it is nonconvex while the R-convex hull is always convex. We note that the
$\alpha$
-convex hull of a finite sample is different from its R-spindle-convex hull as it is nonconvex while the R-convex hull is always convex. We note that the
![]() $\alpha$
-convex hull can be used to estimate not necessarily convex sets as well; see [Reference Pateiro López21, Reference Pateiro-López and Rodrguez-Casal22, Reference Rodríguez Casal28], where several such results are proved about random samples chosen from the set according to an absolute continuous probability distribution.
$\alpha$
-convex hull can be used to estimate not necessarily convex sets as well; see [Reference Pateiro López21, Reference Pateiro-López and Rodrguez-Casal22, Reference Rodríguez Casal28], where several such results are proved about random samples chosen from the set according to an absolute continuous probability distribution.
A convex R-disc-polygon is clearly R-spindle convex. We also consider a single radius-R disc and a single point as R-disc-polygons, albeit trivial ones. The nonsmooth points of the boundary of a nontrivial convex R-disc-polygon are called vertices. The vertices divide the boundary into a union of radius-R circular arcs of positive arc length that we call edges. Thus, a nontrivial convex R-disc-polygon has an equal number of edges and vertices, just like a classical convex polygon, except the sides are radius-R circular arcs. The radius-R disc has one edge and no vertex, and a single point has one vertex and no side.
Our probability model is the following. Let K be a convex body in
![]() $\mathbb{R}^2$
with an at least
$\mathbb{R}^2$
with an at least
![]() $C^{2}_+$
-smooth boundary, and let R be such that
$C^{2}_+$
-smooth boundary, and let R be such that
![]() $\kappa(x)>1/R$
for all
$\kappa(x)>1/R$
for all
![]() $x\in\partial K$
. Let
$x\in\partial K$
. Let
![]() $x_1, \ldots, x_n$
be independent random points in K chosen according to the uniform probability distribution. The R-spindle-convex hull
$x_1, \ldots, x_n$
be independent random points in K chosen according to the uniform probability distribution. The R-spindle-convex hull
![]() $K_n^R=[x_1,\ldots, x_n]_R$
is called a uniform random R-disc-polygon in K, and is a convex R-disc-polygon. It is clear that
$K_n^R=[x_1,\ldots, x_n]_R$
is called a uniform random R-disc-polygon in K, and is a convex R-disc-polygon. It is clear that
![]() $K_n^R$
has an equal number of vertices and sides with probability 1, and its vertex set is formed by some of the random points
$K_n^R$
has an equal number of vertices and sides with probability 1, and its vertex set is formed by some of the random points
![]() $x_1,\ldots, x_n$
. Let
$x_1,\ldots, x_n$
. Let
![]() $f_0(K_n^R)$
denote the number of vertices of
$f_0(K_n^R)$
denote the number of vertices of
![]() $K_n^R$
. We note that in [Reference Pateiro López21] the radius
$K_n^R$
. We note that in [Reference Pateiro López21] the radius
![]() $r_n$
of the discs used in the estimation of an
$r_n$
of the discs used in the estimation of an
![]() $\alpha$
-convex set tends to zero as
$\alpha$
-convex set tends to zero as
![]() $n\to\infty$
. In our model, we use suitable fixed-radius discs in order to guarantee that the R-spindle-convex hull of the random sample is contained in K. However, after the statements of our main results, we briefly discuss what happens to the quality of the approximation when the radius R tends to the limits of its possible range.
$n\to\infty$
. In our model, we use suitable fixed-radius discs in order to guarantee that the R-spindle-convex hull of the random sample is contained in K. However, after the statements of our main results, we briefly discuss what happens to the quality of the approximation when the radius R tends to the limits of its possible range.
It was proved in [Reference Fodor, Kevei and Vígh11, Theorem 1.1, p. 901] that under the above conditions, as
![]() $n\to\infty$
,
$n\to\infty$
,
where
 $$z_1(K) = \sqrt[3]{\frac 2{3A(K)}}\cdot\Gamma\bigg(\frac53\bigg)\int_{\partial K}\bigg(\kappa(x)-\frac{1}{R}\bigg)^{1/3}\,\textrm{d}x,$$
$$z_1(K) = \sqrt[3]{\frac 2{3A(K)}}\cdot\Gamma\bigg(\frac53\bigg)\int_{\partial K}\bigg(\kappa(x)-\frac{1}{R}\bigg)^{1/3}\,\textrm{d}x,$$
and A(K) denotes the area of K.
We note that (2) and (3) are connected by an Efron-type [Reference Efron10] identity [Reference Fodor, Kevei and Vígh11, (5.10), p. 910], which states that
In this paper we prove the following theorems that provide power-series expansions of
![]() $\mathbb{E} (f_0(K_n^R))$
and
$\mathbb{E} (f_0(K_n^R))$
and
![]() $\mathbb{E} (A(K\setminus K_{n}^R))$
in the case when
$\mathbb{E} (A(K\setminus K_{n}^R))$
in the case when
![]() $\partial K$
satisfies stronger differentiability conditions.
$\partial K$
satisfies stronger differentiability conditions.
Theorem 2. Let
![]() $k\geq 2$
be an integer, and let K be a convex body in
$k\geq 2$
be an integer, and let K be a convex body in
![]() $\mathbb{R}^2$
with a
$\mathbb{R}^2$
with a
![]() $C^{k+1}_+$
-smooth boundary. Then, for all
$C^{k+1}_+$
-smooth boundary. Then, for all
![]() $R>\max_{x\in\partial K} 1/\kappa (x)$
,
$R>\max_{x\in\partial K} 1/\kappa (x)$
,
as
![]() $n\to\infty$
. All the coefficients
$n\to\infty$
. All the coefficients
![]() $z_1,\ldots, z_k$
can be determined explicitly. In particular,
$z_1,\ldots, z_k$
can be determined explicitly. In particular,
 \begin{align*} z_1(K) & = \sqrt[3]{\frac{2}{3A(K)}}\Gamma\bigg(\frac53\bigg) \int_{\partial K}\bigg(\kappa(x)-\frac1R\bigg)^{1/3}\,\textrm{d}x, \\[5pt] z_2(K) & = 0, \\[5pt] z_3(K) & = -\Gamma\bigg(\frac73\bigg)\frac{1}{5}\sqrt[3]{\frac{3A(K)}{2}} \int_{\partial K}\bigg(\frac{\kappa''(x)}{3(\kappa(x)-1/R)^{4/3}} + \frac{2R^2\kappa^2(x)+7R\kappa(x)-1}{2R^2(\kappa(x)-1/R)^{1/3}} \\[5pt] & \qquad\qquad\qquad\qquad\qquad\qquad - \frac{5(\kappa'(x))^2}{9(\kappa(x)-1/R)^{7/3}}\bigg)\,\textrm{d}x. \end{align*}
\begin{align*} z_1(K) & = \sqrt[3]{\frac{2}{3A(K)}}\Gamma\bigg(\frac53\bigg) \int_{\partial K}\bigg(\kappa(x)-\frac1R\bigg)^{1/3}\,\textrm{d}x, \\[5pt] z_2(K) & = 0, \\[5pt] z_3(K) & = -\Gamma\bigg(\frac73\bigg)\frac{1}{5}\sqrt[3]{\frac{3A(K)}{2}} \int_{\partial K}\bigg(\frac{\kappa''(x)}{3(\kappa(x)-1/R)^{4/3}} + \frac{2R^2\kappa^2(x)+7R\kappa(x)-1}{2R^2(\kappa(x)-1/R)^{1/3}} \\[5pt] & \qquad\qquad\qquad\qquad\qquad\qquad - \frac{5(\kappa'(x))^2}{9(\kappa(x)-1/R)^{7/3}}\bigg)\,\textrm{d}x. \end{align*}
By the spindle-convex version of Efron’s identity we obtain the following corollary.
Theorem 3. Let
![]() $k\geq 2$
be an integer, and let K be a convex body in
$k\geq 2$
be an integer, and let K be a convex body in
![]() $\mathbb{R}^2$
with a
$\mathbb{R}^2$
with a
![]() $C^{k+1}_+$
-smooth boundary. Then, for all
$C^{k+1}_+$
-smooth boundary. Then, for all
![]() $R>\max_{x\in\partial K} 1/\kappa (x)$
,
$R>\max_{x\in\partial K} 1/\kappa (x)$
,
as
![]() $n\to\infty$
, where
$n\to\infty$
, where
![]() $z_i'(K)=A(K)z_i(K)$
for
$z_i'(K)=A(K)z_i(K)$
for
![]() $i=1,\ldots, k$
.
$i=1,\ldots, k$
.
We note that we only evaluate
![]() $z_i(K)$
,
$z_i(K)$
,
![]() $i=1,2,3$
, explicitly in this paper because the calculation, although possible, becomes more complicated as i increases, even when K is a closed disc. The coefficients
$i=1,2,3$
, explicitly in this paper because the calculation, although possible, becomes more complicated as i increases, even when K is a closed disc. The coefficients
![]() $z_i(K)$
depend only on R, the area of K, and on the power-series expansion of the local representation of the boundary of K, see (6); in particular, on the derivatives of
$z_i(K)$
depend only on R, the area of K, and on the power-series expansion of the local representation of the boundary of K, see (6); in particular, on the derivatives of
![]() $\kappa$
up to order
$\kappa$
up to order
![]() $i-1$
.
$i-1$
.
Although Theorems 2 and 3 are only valid for
![]() $R>R_\textrm{M}=\max_{x\in\partial K} 1/\kappa(x)$
, it may also be interesting to look at the behaviour of the coefficients
$R>R_\textrm{M}=\max_{x\in\partial K} 1/\kappa(x)$
, it may also be interesting to look at the behaviour of the coefficients
![]() $z_i(K)$
at the limits of the range of R. When
$z_i(K)$
at the limits of the range of R. When
![]() $R\to\infty$
, the integral in
$R\to\infty$
, the integral in
![]() $z_1(K)$
tends to the affine arc length of
$z_1(K)$
tends to the affine arc length of
![]() $\partial K$
[Reference Fodor, Kevei and Vígh11]. For
$\partial K$
[Reference Fodor, Kevei and Vígh11]. For
![]() $z_3(K)$
, direct calculation yields
$z_3(K)$
, direct calculation yields
where k(x) is the affine curvature of
![]() $\partial K$
at x, cf. also (1).
$\partial K$
at x, cf. also (1).
On the other hand, when
![]() $R\to R_\textrm{M}^+$
, then
$R\to R_\textrm{M}^+$
, then
 \begin{equation*} \lim_{R\to R_M^+}z_1(K) = \sqrt[3]{\frac{2}{3A(K)}}\Gamma\bigg(\frac53\bigg) \int_{\partial K}\bigg(\kappa(x)-\frac{1}{R_\textrm{M}}\bigg)^{1/3}\,\textrm{d}x, \end{equation*}
\begin{equation*} \lim_{R\to R_M^+}z_1(K) = \sqrt[3]{\frac{2}{3A(K)}}\Gamma\bigg(\frac53\bigg) \int_{\partial K}\bigg(\kappa(x)-\frac{1}{R_\textrm{M}}\bigg)^{1/3}\,\textrm{d}x, \end{equation*}
where the integrand is bounded, nonnegative, and zero in exactly those points where
![]() $\kappa(x)=1/R_\textrm{M}$
. We conjecture that the right-hand side is equal to
$\kappa(x)=1/R_\textrm{M}$
. We conjecture that the right-hand side is equal to
![]() $\lim_{n\to\infty}\mathbb{E}f_0(K_n^R))n^{-1/3}$
when
$\lim_{n\to\infty}\mathbb{E}f_0(K_n^R))n^{-1/3}$
when
![]() $R=R_\textrm{M}$
and K is not a closed disc. However, this asymptotic expectation is not known. We also note that
$R=R_\textrm{M}$
and K is not a closed disc. However, this asymptotic expectation is not known. We also note that
![]() $z_1(K)$
is a monotonically decreasing function of R, which shows that it is indeed more advantageous to use circular arcs to form the hull of the random sample of n points in order to approximate K better. Although the order of magnitude in n of the approximation is the same as in the linearly convex case, the main coefficient is smaller.
$z_1(K)$
is a monotonically decreasing function of R, which shows that it is indeed more advantageous to use circular arcs to form the hull of the random sample of n points in order to approximate K better. Although the order of magnitude in n of the approximation is the same as in the linearly convex case, the main coefficient is smaller.
Furthermore, we note that in the particular case when
![]() $K=B^2$
and
$K=B^2$
and
![]() $R>1$
,
$R>1$
,
 \begin{align*} z_1(B) & = \sqrt[3]{\frac{2}{3\pi}}\Gamma\bigg(\frac53\bigg)2\pi\bigg(1-\frac{1}{R}\bigg)^{1/3}, \\[5pt] z_2(B) & = 0, \\[5pt] z_3(B) & = -\Gamma\bigg(\frac73\bigg)\frac{1}{5}\sqrt[3]{\frac{3\pi}{2}}2\pi\frac{2R^2+7R-1}{2R^2(1-1/R)^{1/3}}.\end{align*}
\begin{align*} z_1(B) & = \sqrt[3]{\frac{2}{3\pi}}\Gamma\bigg(\frac53\bigg)2\pi\bigg(1-\frac{1}{R}\bigg)^{1/3}, \\[5pt] z_2(B) & = 0, \\[5pt] z_3(B) & = -\Gamma\bigg(\frac73\bigg)\frac{1}{5}\sqrt[3]{\frac{3\pi}{2}}2\pi\frac{2R^2+7R-1}{2R^2(1-1/R)^{1/3}}.\end{align*}
If
![]() $R\to 1^+$
then
$R\to 1^+$
then
![]() $z_1(B)\to 0$
and
$z_1(B)\to 0$
and
![]() $z_3(B)\to -\infty$
, and both are monotonically increasing functions showing that the quality of approximation improves as R tends to 1. This behaviour comes as no surprise as the expected number of vertices behaves fundamentally differently from the previously discussed situation when
$z_3(B)\to -\infty$
, and both are monotonically increasing functions showing that the quality of approximation improves as R tends to 1. This behaviour comes as no surprise as the expected number of vertices behaves fundamentally differently from the previously discussed situation when
![]() $K\neq B$
; the order of magnitude in n is different if
$K\neq B$
; the order of magnitude in n is different if
![]() $K=B$
, as we will see below. Finally, we note that we also suspect that
$K=B$
, as we will see below. Finally, we note that we also suspect that
![]() $z_3(K)$
behaves similarly to
$z_3(K)$
behaves similarly to
![]() $z_3(B)$
when
$z_3(B)$
when
![]() $R\to R_\textrm{M}^+$
, but this is not clear from its current form.
$R\to R_\textrm{M}^+$
, but this is not clear from its current form.
It was proved in [Reference Fodor, Kevei and Vígh11] that
as
![]() $n\to\infty$
. The unusual behaviour of
$n\to\infty$
. The unusual behaviour of
![]() $\mathbb{E} (f_0(B(R)_n^R))$
, i.e. that it tends to a finite constant, was explained in [Reference Marynych and Molchanov20], which proved, in the much wider context of L-convexity (see also [Reference Fodor, Papvári and Vígh12]), that
$\mathbb{E} (f_0(B(R)_n^R))$
, i.e. that it tends to a finite constant, was explained in [Reference Marynych and Molchanov20], which proved, in the much wider context of L-convexity (see also [Reference Fodor, Papvári and Vígh12]), that
![]() $\mathbb{E} (f_0(B(R)_n^R))$
tends to the expectation of the number of vertices of the polar of the zero cell of a Poisson line process whose intensity measure on
$\mathbb{E} (f_0(B(R)_n^R))$
tends to the expectation of the number of vertices of the polar of the zero cell of a Poisson line process whose intensity measure on
![]() $\mathbb{R}$
is
$\mathbb{R}$
is
![]() $A(B(R))^{-1}=1/(R^2\pi)$
times the Lebesgue measure, and whose directional distribution is uniform on
$A(B(R))^{-1}=1/(R^2\pi)$
times the Lebesgue measure, and whose directional distribution is uniform on
![]() $S^1$
[Reference Marynych and Molchanov20, (6.1), p. 29]. In Section 4, we calculate (the first three terms of) the power-series expansion of
$S^1$
[Reference Marynych and Molchanov20, (6.1), p. 29]. In Section 4, we calculate (the first three terms of) the power-series expansion of
![]() $\mathbb{E} (f_0(B(R)_n^R))$
for the sake of completeness. This gives the speed of convergence of
$\mathbb{E} (f_0(B(R)_n^R))$
for the sake of completeness. This gives the speed of convergence of
![]() $\mathbb{E} (f_0(B(R)_n^R))$
to
$\mathbb{E} (f_0(B(R)_n^R))$
to
![]() $\pi^2/2$
. We note that here we only quoted the result from [Reference Marynych and Molchanov20] in the plane; however, it was proved in
$\pi^2/2$
. We note that here we only quoted the result from [Reference Marynych and Molchanov20] in the plane; however, it was proved in
![]() $\mathbb{R}^d$
.
$\mathbb{R}^d$
.
The rest of the paper is organised as follows. In Section 2, we briefly recall from [Reference Fodor, Kevei and Vígh11] the necessary background and describe how
![]() $\mathbb{E}(f_0(B(R)_n^R))$
can be calculated. In Section 3, we provide the power-series expansions of the involved geometric quantities. In Section 4, we quote a power-series expansion of the incomplete beta function from [Reference Gruber14]. We prove Theorem 2 in Section 5. Finally, in Section 6, we treat the case when
$\mathbb{E}(f_0(B(R)_n^R))$
can be calculated. In Section 3, we provide the power-series expansions of the involved geometric quantities. In Section 4, we quote a power-series expansion of the incomplete beta function from [Reference Gruber14]. We prove Theorem 2 in Section 5. Finally, in Section 6, we treat the case when
![]() $K=B(R)$
.
$K=B(R)$
.
2. Expectation of the number of vertices of
 $K_n^R$
$K_n^R$
Our arguments are based on the methods of [Reference Gruber14, Reference Rényi and Sulanke26]. We also note that, compared to those of [Reference Pateiro López21], our methods essentially depend on the higher regularity and smoothness of the boundary of K and the explicit local power-series expansion of
![]() $\partial K$
. Notice that it is enough to prove the theorem for
$\partial K$
. Notice that it is enough to prove the theorem for
![]() $R=1$
; from that, the statement for general R follows by a scaling argument.
$R=1$
; from that, the statement for general R follows by a scaling argument.
Due to the
![]() $C^{k+1}_+$
condition, K is both smooth, i.e. has a unique supporting line at each boundary point, and strictly convex. Let
$C^{k+1}_+$
condition, K is both smooth, i.e. has a unique supporting line at each boundary point, and strictly convex. Let
![]() $u_x\in S^1$
denote the unique outer unit normal vector to K at x, and for
$u_x\in S^1$
denote the unique outer unit normal vector to K at x, and for
![]() $u\in S^1$
let
$u\in S^1$
let
![]() $x_u$
be the (again) unique boundary point where the outer unit normal is equal to u.
$x_u$
be the (again) unique boundary point where the outer unit normal is equal to u.
We use
![]() $B^\circ$
to denote the interior of B. A subset D of K is a disc-cap of K if
$B^\circ$
to denote the interior of B. A subset D of K is a disc-cap of K if
![]() $D=K\setminus (B^\circ+p)$
for some point
$D=K\setminus (B^\circ+p)$
for some point
![]() $p\in\mathbb{R}^2$
. It was proved in [Reference Fodor, Kevei and Vígh11] that for a disc-cap of K,
$p\in\mathbb{R}^2$
. It was proved in [Reference Fodor, Kevei and Vígh11] that for a disc-cap of K,
![]() $D=K\setminus (B^\circ+p)$
, there exists a unique point
$D=K\setminus (B^\circ+p)$
, there exists a unique point
![]() $x_0\in \partial K \cap D$
and
$x_0\in \partial K \cap D$
and
![]() $t\geq 0$
such that
$t\geq 0$
such that
![]() $B+p=B+x_0-(1+t) u_{x_0}$
. We call
$B+p=B+x_0-(1+t) u_{x_0}$
. We call
![]() $x_0$
the vertex and t the height of D.
$x_0$
the vertex and t the height of D.
We may assume that
![]() $o\in\textrm{int}\,K$
. Let
$o\in\textrm{int}\,K$
. Let
![]() $A=A(K)=V_2(K)$
. Let
$A=A(K)=V_2(K)$
. Let
![]() $X_n=\{x_1, \ldots, x_n\}$
be a sample of independent and identically distributed uniform random points from K. For
$X_n=\{x_1, \ldots, x_n\}$
be a sample of independent and identically distributed uniform random points from K. For
![]() $x_i, x_j\in X_n$
, we denote by
$x_i, x_j\in X_n$
, we denote by
![]() $x_ix_j$
the shorter unit circular arc connecting
$x_ix_j$
the shorter unit circular arc connecting
![]() $x_i$
and
$x_i$
and
![]() $x_j$
with the property that
$x_j$
with the property that
![]() $x_i$
and
$x_i$
and
![]() $x_j$
are in counterclockwise order on the arc. Let
$x_j$
are in counterclockwise order on the arc. Let
be the set of directed edges of
![]() $K_n^1$
. For
$K_n^1$
. For
![]() $x_i, x_j\in X_n$
, let
$x_i, x_j\in X_n$
, let
![]() $C_{ij}$
be the disc-cap of K determined by the disc of
$C_{ij}$
be the disc-cap of K determined by the disc of
![]() $x_ix_j$
, and
$x_ix_j$
, and
![]() $A_{ij}=A(C_{ij})$
. Note that
$A_{ij}=A(C_{ij})$
. Note that
![]() $x_ix_j\in\mathcal{E}(K_n^1)$
exactly when all the other
$x_ix_j\in\mathcal{E}(K_n^1)$
exactly when all the other
![]() $n-2$
random points of
$n-2$
random points of
![]() $X_n$
are in
$X_n$
are in
![]() $K\setminus C_{ij}$
. Thus, due to the independence of the random points,
$K\setminus C_{ij}$
. Thus, due to the independence of the random points,
 \begin{align} \mathbb{E} (f_0(K_n^1)) & = \sum\frac{1}{A^n} \int_K\cdots\int_K\mathbf 1\{x_ix_j\in\mathcal E(K_n^1)\}\,\textrm{d}x_1\cdots\textrm{d}x_n \notag \\[5pt] & = \left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac1{A^2}\int_K\int_K\bigg(1-\frac{A_{12}}{A}\bigg)^{n-2} + \bigg(1-\frac{A_{21}}{A}\bigg)^{n-2}\,\textrm{d}x_1\,\textrm{d}x_2, \end{align}
\begin{align} \mathbb{E} (f_0(K_n^1)) & = \sum\frac{1}{A^n} \int_K\cdots\int_K\mathbf 1\{x_ix_j\in\mathcal E(K_n^1)\}\,\textrm{d}x_1\cdots\textrm{d}x_n \notag \\[5pt] & = \left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac1{A^2}\int_K\int_K\bigg(1-\frac{A_{12}}{A}\bigg)^{n-2} + \bigg(1-\frac{A_{21}}{A}\bigg)^{n-2}\,\textrm{d}x_1\,\textrm{d}x_2, \end{align}
where in the first line the summation extends over all ordered pairs of distinct points from
![]() $X_n$
. Now, we use the same reparametrization for the pair
$X_n$
. Now, we use the same reparametrization for the pair
![]() $(x_1, x_2)$
as in [Reference Fodor, Kevei and Vígh11]. Let
$(x_1, x_2)$
as in [Reference Fodor, Kevei and Vígh11]. Let
![]() $(x_1, x_2)=\Phi (u, t, u_1, u_2)$
, where
$(x_1, x_2)=\Phi (u, t, u_1, u_2)$
, where
![]() $u, u_1, u_2\in S^1$
and
$u, u_1, u_2\in S^1$
and
![]() $0\leq t\leq t_0(u)$
are chosen such that
$0\leq t\leq t_0(u)$
are chosen such that
![]() $C(u,t)=C_{12}$
, where C(u, t) is the unique disc-cap of K with vertex
$C(u,t)=C_{12}$
, where C(u, t) is the unique disc-cap of K with vertex
![]() $x_u$
and height t, and
$x_u$
and height t, and
The vectors
![]() $u_1$
and
$u_1$
and
![]() $u_2$
are the unique outer unit normals of
$u_2$
are the unique outer unit normals of
![]() $\partial B+x_u-(1+t)u$
at
$\partial B+x_u-(1+t)u$
at
![]() $x_1$
and
$x_1$
and
![]() $x_2$
, respectively. For fixed u and t, both
$x_2$
, respectively. For fixed u and t, both
![]() $u_1$
and
$u_1$
and
![]() $u_2$
are contained in the same arc L(u, t) of
$u_2$
are contained in the same arc L(u, t) of
![]() $S^1$
, whose length is denoted by
$S^1$
, whose length is denoted by
![]() $\ell(u,t)$
. The uniqueness of the vertex and height of disc-caps guarantees that the map
$\ell(u,t)$
. The uniqueness of the vertex and height of disc-caps guarantees that the map
![]() $\Phi$
is well defined, bijective, and differentiable on a suitable domain of
$\Phi$
is well defined, bijective, and differentiable on a suitable domain of
![]() $(u, t, u_1, u_2)$
. The Jacobian of
$(u, t, u_1, u_2)$
. The Jacobian of
![]() $\Phi$
is
$\Phi$
is
Let A(u, t) denote the area of the disc-cap with vertex
![]() $x_u$
and height t. For each
$x_u$
and height t. For each
![]() $u\in S^1$
, let
$u\in S^1$
, let
![]() $t_0(u)$
be maximal such that
$t_0(u)$
be maximal such that
![]() $A(u,t_0(u))\geq 0$
. Then, after the change of variables, from (4) we get
$A(u,t_0(u))\geq 0$
. Then, after the change of variables, from (4) we get
 \begin{align*} \mathbb{E}(f_0(K_n^1)) & = \binom{n}{2}\frac1{A^2}\int_{S^1}\int_0^{t_0(u)}\int_{L(u,t)}\int_{L(u,t)}\bigg(1-\frac{A(u,t)}{A}\bigg)^{n-2} \\[5pt] & \qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \times \bigg(1+t-\frac{1}{\kappa(x_u)}\bigg)|u_1\times u_2|\,\textrm{d}u_1\,\textrm{d}u_2\,\textrm{d}t\,\textrm{d}u \\[5pt] & = \left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac1{A^2}\int_{S^1}\int_0^{t_0(u)}\bigg(1-\frac{A(u,t)}{A}\bigg)^{n-2}J(u,t)\, \textrm{d}t\,\textrm{d}u,\end{align*}
\begin{align*} \mathbb{E}(f_0(K_n^1)) & = \binom{n}{2}\frac1{A^2}\int_{S^1}\int_0^{t_0(u)}\int_{L(u,t)}\int_{L(u,t)}\bigg(1-\frac{A(u,t)}{A}\bigg)^{n-2} \\[5pt] & \qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \times \bigg(1+t-\frac{1}{\kappa(x_u)}\bigg)|u_1\times u_2|\,\textrm{d}u_1\,\textrm{d}u_2\,\textrm{d}t\,\textrm{d}u \\[5pt] & = \left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac1{A^2}\int_{S^1}\int_0^{t_0(u)}\bigg(1-\frac{A(u,t)}{A}\bigg)^{n-2}J(u,t)\, \textrm{d}t\,\textrm{d}u,\end{align*}
where
 \begin{align*} J(u,t) & = \bigg(1+t-\frac{1}{\kappa(x_u)}\bigg)\int_{L(u,t)}\int_{L(u,t)}|u_1\times u_2|\,\textrm{d}u_1\,\textrm{d}u_2 \\[5pt] & = 2\bigg(1+t-\frac{1}{\kappa(x_u)}\bigg)(\ell(u,t)-\sin \ell(u,t)).\end{align*}
\begin{align*} J(u,t) & = \bigg(1+t-\frac{1}{\kappa(x_u)}\bigg)\int_{L(u,t)}\int_{L(u,t)}|u_1\times u_2|\,\textrm{d}u_1\,\textrm{d}u_2 \\[5pt] & = 2\bigg(1+t-\frac{1}{\kappa(x_u)}\bigg)(\ell(u,t)-\sin \ell(u,t)).\end{align*}
We note that due to the
![]() $C^2_+$
property of
$C^2_+$
property of
![]() $\partial K$
,
$\partial K$
,
![]() $J(u,t)\leq C$
for some
$J(u,t)\leq C$
for some
![]() $0<C\leq 6(2\pi+1)$
that depends only on K.
$0<C\leq 6(2\pi+1)$
that depends only on K.
Let
![]() $0<\delta<A$
be an arbitrary but fixed small number. Let
$0<\delta<A$
be an arbitrary but fixed small number. Let
![]() $0<t_1$
be such that, for arbitrary
$0<t_1$
be such that, for arbitrary
![]() $t\in [t_1, t_0(u)]$
and
$t\in [t_1, t_0(u)]$
and
![]() $u\in S^1$
,
$u\in S^1$
,
![]() $A(u,t)\geq \delta$
. Then
$A(u,t)\geq \delta$
. Then
 \begin{align*} \int_{S^1}\int_{t_1}^{t_0(u)}\bigg(1-\frac{A(u,t)}{A}\bigg)^{n-2}J(u,t)\,\textrm{d}t\,\textrm{d}u & \leq C\int_{S^1}\int_{t_1}^{t_0(u)}\bigg(1-\frac{A(u,t)}{A}\bigg)^{n-2}\,\textrm{d}t\,\textrm{d}u \\[5pt] & \leq 2\pi C\int_{t_1}^{2}\bigg(1-\frac{\delta}{A}\bigg)^{n-2}\,\textrm{d}t \\[5pt] & \leq 4\pi C\bigg(1-\frac{\delta}{A}\bigg)^{n-2},\end{align*}
\begin{align*} \int_{S^1}\int_{t_1}^{t_0(u)}\bigg(1-\frac{A(u,t)}{A}\bigg)^{n-2}J(u,t)\,\textrm{d}t\,\textrm{d}u & \leq C\int_{S^1}\int_{t_1}^{t_0(u)}\bigg(1-\frac{A(u,t)}{A}\bigg)^{n-2}\,\textrm{d}t\,\textrm{d}u \\[5pt] & \leq 2\pi C\int_{t_1}^{2}\bigg(1-\frac{\delta}{A}\bigg)^{n-2}\,\textrm{d}t \\[5pt] & \leq 4\pi C\bigg(1-\frac{\delta}{A}\bigg)^{n-2},\end{align*}
and thus, in particular, with a suitably small choice of
![]() $\delta$
,
$\delta$
,
In the following sections we evaluate the integral (5) under different smoothness assumptions on
![]() $\partial K$
.
$\partial K$
.
3. Power-series expansions
Let
![]() $k\geq 2$
be an integer and
$k\geq 2$
be an integer and
![]() $K\subset\mathbb{R}^2$
a convex body with a
$K\subset\mathbb{R}^2$
a convex body with a
![]() $C^{k+1}_+$
boundary (
$C^{k+1}_+$
boundary (
![]() $(k+1)$
times continuously differentiable with everywhere positive curvature). We will use the following statement from [Reference Gruber14] (see also [Reference Schneider29]). We state it in the form used in [Reference Reitzner24], but only for
$(k+1)$
times continuously differentiable with everywhere positive curvature). We will use the following statement from [Reference Gruber14] (see also [Reference Schneider29]). We state it in the form used in [Reference Reitzner24], but only for
![]() $d=2$
.
$d=2$
.
Lemma 1. Let K be a convex body in
![]() $\mathbb{R}^2$
with a
$\mathbb{R}^2$
with a
![]() $C^{k+1}_+$
boundary for some integer
$C^{k+1}_+$
boundary for some integer
![]() $k\geq 2$
. Then there exist constants
$k\geq 2$
. Then there exist constants
![]() $\alpha, \beta>0$
depending only on K such that the following holds for every boundary point x of K. If
$\alpha, \beta>0$
depending only on K such that the following holds for every boundary point x of K. If
![]() $x=0$
and the (unique) tangent line of K at x is
$x=0$
and the (unique) tangent line of K at x is
![]() $\mathbb{R}$
, then there is an
$\mathbb{R}$
, then there is an
![]() $\alpha$
-neighbourhood of x in which the boundary of K can be represented by a convex function
$\alpha$
-neighbourhood of x in which the boundary of K can be represented by a convex function
![]() $f(\sigma)$
of differentiability class
$f(\sigma)$
of differentiability class
![]() $C^{k+1}$
in
$C^{k+1}$
in
![]() $\mathbb{R}$
. Moreover, all derivatives of f up to order
$\mathbb{R}$
. Moreover, all derivatives of f up to order
![]() $k+1$
are uniformly bounded by
$k+1$
are uniformly bounded by
![]() $\beta$
.
$\beta$
.
Let
![]() $u\in S^1$
and let
$u\in S^1$
and let
![]() $x=x_u\in\partial K$
. Assume that K is in the position described in Lemma 1. Let f be the function that represents the boundary of K in an
$x=x_u\in\partial K$
. Assume that K is in the position described in Lemma 1. Let f be the function that represents the boundary of K in an
![]() $\alpha$
-neighbourhood of x. Then f is of the form
$\alpha$
-neighbourhood of x. Then f is of the form
![]() $f(\sigma) = b_2(u)\sigma^2 + \cdots + b_k(u)\sigma^k + O(\sigma^{k+1})$
, where the coefficients
$f(\sigma) = b_2(u)\sigma^2 + \cdots + b_k(u)\sigma^k + O(\sigma^{k+1})$
, where the coefficients
![]() $b_i=b_i(u)$
,
$b_i=b_i(u)$
,
![]() $i=2,\ldots, k$
, depend on u. We will suppress the dependence of coefficients on u (and thus on x) when we work with a fixed u. We will only indicate dependence when u is used in the argument.
$i=2,\ldots, k$
, depend on u. We will suppress the dependence of coefficients on u (and thus on x) when we work with a fixed u. We will only indicate dependence when u is used in the argument.
We recall the following facts from the differential geometry of plane curves. Let r(s) be the arc-length parametrization of
![]() $\partial K$
with
$\partial K$
with
![]() $r(0)=x$
in the neighbourhood of x such that the following hold. With the above assumptions on K, let the vector
$r(0)=x$
in the neighbourhood of x such that the following hold. With the above assumptions on K, let the vector
![]() $r^{\prime}(0)$
and the unit normal vector
$r^{\prime}(0)$
and the unit normal vector
![]() $r''(0)/\kappa(0)=-u$
form the basis of a Cartesian coordinate system, in which we denote the coordinate along the
$r''(0)/\kappa(0)=-u$
form the basis of a Cartesian coordinate system, in which we denote the coordinate along the
![]() $r^{\prime}$
-axis by
$r^{\prime}$
-axis by
![]() $\sigma$
, and the
$\sigma$
, and the
![]() $r^{\prime\prime}$
-axis by
$r^{\prime\prime}$
-axis by
![]() $\eta$
. Then
$\eta$
. Then
 \begin{equation} \begin{aligned} \sigma = \sigma(s) & = s-\frac{\kappa^2(0)}{3!}s^3-3\kappa(0)\kappa'(0)\frac{s^4}{4!}+O(s^5), \\[5pt] \eta = \eta(s) & = \kappa(0)\frac{s^2}{2}+\kappa'(0)\frac{s^3}{3!}+(\kappa''(0)-\kappa^3(0))\frac{s^4}{4!}+O(s^5); \end{aligned}\end{equation}
\begin{equation} \begin{aligned} \sigma = \sigma(s) & = s-\frac{\kappa^2(0)}{3!}s^3-3\kappa(0)\kappa'(0)\frac{s^4}{4!}+O(s^5), \\[5pt] \eta = \eta(s) & = \kappa(0)\frac{s^2}{2}+\kappa'(0)\frac{s^3}{3!}+(\kappa''(0)-\kappa^3(0))\frac{s^4}{4!}+O(s^5); \end{aligned}\end{equation}
see, for example, [Reference Do Carmo9, Section 1.6]. From the equality
![]() $f(\sigma(s))=\eta(s)$
we can identify the coefficients
$f(\sigma(s))=\eta(s)$
we can identify the coefficients
![]() $b_2,\ldots, b_k$
. In particular,
$b_2,\ldots, b_k$
. In particular,
With a slight abuse of notation, in the above formulas we use
![]() $\kappa$
to denote the curvature as a function of s, which is different from the previous usage. Later, we will also use the same letter when the curvature is a function of the outer unit normal u. Moreover, when u (s or x) is fixed, we suppress the dependence of
$\kappa$
to denote the curvature as a function of s, which is different from the previous usage. Later, we will also use the same letter when the curvature is a function of the outer unit normal u. Moreover, when u (s or x) is fixed, we suppress the dependence of
![]() $\kappa$
on u (s or x). It will always be clear from the context which function we consider.
$\kappa$
on u (s or x). It will always be clear from the context which function we consider.
We will also use the following statement due to [Reference Gruber14], see also [Reference Reitzner24]. (We state it again only for
![]() $d=2$
, so this is a simpler version of the original theorem.)
$d=2$
, so this is a simpler version of the original theorem.)
Lemma 2. Let
![]() $\eta = \eta(\sigma) = b_m\sigma^m + \cdots + b_{k}\sigma^k + O(\sigma^{k+1})$
for
$\eta = \eta(\sigma) = b_m\sigma^m + \cdots + b_{k}\sigma^k + O(\sigma^{k+1})$
for
![]() $0\leq\sigma\leq\alpha$
,
$0\leq\sigma\leq\alpha$
,
![]() $2\leq m\leq k$
, be a strictly increasing function. Then there are coefficients
$2\leq m\leq k$
, be a strictly increasing function. Then there are coefficients
![]() $c_1, \ldots, c_{k-m+1}$
and a constant
$c_1, \ldots, c_{k-m+1}$
and a constant
![]() $\gamma>0$
such that the inverse function
$\gamma>0$
such that the inverse function
![]() $\sigma=\sigma(\eta)$
has the representation
$\sigma=\sigma(\eta)$
has the representation
for
![]() $0\leq\eta\leq\gamma$
. The coefficients
$0\leq\eta\leq\gamma$
. The coefficients
![]() $c_1,\ldots, c_{k-m+1}$
can be determined explicitly in terms of
$c_1,\ldots, c_{k-m+1}$
can be determined explicitly in terms of
![]() $b_m,\ldots, b_{k}$
. In particular,
$b_m,\ldots, b_{k}$
. In particular,
For
![]() $t\geq 0$
, let the unit-radius lower semicircle with centre
$t\geq 0$
, let the unit-radius lower semicircle with centre
![]() $(0,1+t)$
be represented by the function
$(0,1+t)$
be represented by the function
 \begin{equation*} g_t(\sigma) = t + 1 - \sqrt{1-\sigma^2} = t + 1 - \sum_{i=0}^{\infty}(\!-\!1)^i\left(\begin{array}{c}{\frac{1}{2}}\\[2pt] {i}\end{array}\right)\sigma^{2i} = t + g_2\sigma^2 + \cdots + g_{2i}\sigma^{2i} + \cdots\end{equation*}
\begin{equation*} g_t(\sigma) = t + 1 - \sqrt{1-\sigma^2} = t + 1 - \sum_{i=0}^{\infty}(\!-\!1)^i\left(\begin{array}{c}{\frac{1}{2}}\\[2pt] {i}\end{array}\right)\sigma^{2i} = t + g_2\sigma^2 + \cdots + g_{2i}\sigma^{2i} + \cdots\end{equation*}
for
![]() $\sigma\in [\!-\!1,1]$
, where
$\sigma\in [\!-\!1,1]$
, where
![]() $g_2=\frac 12$
,
$g_2=\frac 12$
,
![]() $g_3=0$
, and
$g_3=0$
, and
![]() $g_4=\frac 18$
.
$g_4=\frac 18$
.
Let
![]() $\sigma_+=\sigma_+(t)>0$
and
$\sigma_+=\sigma_+(t)>0$
and
![]() $\sigma_-=\sigma_-(t)<0$
such that
$\sigma_-=\sigma_-(t)<0$
such that
![]() $f(\sigma_+)=g_t(\sigma_+)$
and
$f(\sigma_+)=g_t(\sigma_+)$
and
![]() $f(\sigma_-)=g_t(\sigma_-)$
. For sufficiently small
$f(\sigma_-)=g_t(\sigma_-)$
. For sufficiently small
![]() $\sigma>0$
,
$\sigma>0$
,
where, in particular,
![]() $u_2=b_2-g_2$
,
$u_2=b_2-g_2$
,
![]() $u_3=b_3$
, and
$u_3=b_3$
, and
![]() $u_4=b_4-g_4$
.
$u_4=b_4-g_4$
.
Note that we subsequently express coefficients in terms of the
![]() $u_i$
(as long as it does not become too complicated) as they carry all the information about
$u_i$
(as long as it does not become too complicated) as they carry all the information about
![]() $\partial K$
and the circle. We will only substitute their values when we determine our final answer.
$\partial K$
and the circle. We will only substitute their values when we determine our final answer.
Since
![]() $u_2>0$
by the conditions on
$u_2>0$
by the conditions on
![]() $\partial K$
, Lemma 2 yields
$\partial K$
, Lemma 2 yields
where
Similarly, we obtain that
where the coefficients
![]() $\tilde{c}_1,\ldots, \tilde{c}_{k-1}$
can be determined explicitly. In particular,
$\tilde{c}_1,\ldots, \tilde{c}_{k-1}$
can be determined explicitly. In particular,
![]() $\tilde{c}_1=-c_1$
,
$\tilde{c}_1=-c_1$
,
![]() $\tilde{c}_2=c_2$
, and
$\tilde{c}_2=c_2$
, and
![]() $\tilde{c}_3=-c_3$
. Thus, using (7) and (8), the area of the disc cap C(u, t) is
$\tilde{c}_3=-c_3$
. Thus, using (7) and (8), the area of the disc cap C(u, t) is
 \begin{align} A(u,t) & = \int_{\sigma_-}^{\sigma_+}g_t(\sigma) - f(\sigma)\,\textrm{d}\sigma \notag \\[5pt] & =\int_{\sigma_-}^{\sigma_+}t - u_2\sigma^2 - \cdots - u_k\sigma^k + O(\sigma^{k+1})\,\textrm{d}\sigma \notag \\[5pt] & = \bigg[t\sigma - \frac{u_2}{3}\sigma^3 - \cdots - \frac{u_k}{k+1}\sigma^{k+1} + O(\sigma^{k+2})\bigg]_{\sigma_-}^{\sigma_+} \notag \\[5pt] & = a_1t^{3/2} + a_2t^2 + \cdots + a_{k-1}t^{({k+1})/{2}} + O(t^{({k+2})/{2}}), \end{align}
\begin{align} A(u,t) & = \int_{\sigma_-}^{\sigma_+}g_t(\sigma) - f(\sigma)\,\textrm{d}\sigma \notag \\[5pt] & =\int_{\sigma_-}^{\sigma_+}t - u_2\sigma^2 - \cdots - u_k\sigma^k + O(\sigma^{k+1})\,\textrm{d}\sigma \notag \\[5pt] & = \bigg[t\sigma - \frac{u_2}{3}\sigma^3 - \cdots - \frac{u_k}{k+1}\sigma^{k+1} + O(\sigma^{k+2})\bigg]_{\sigma_-}^{\sigma_+} \notag \\[5pt] & = a_1t^{3/2} + a_2t^2 + \cdots + a_{k-1}t^{({k+1})/{2}} + O(t^{({k+2})/{2}}), \end{align}
where the coefficients
![]() $a_1,\ldots, a_{k-1}$
can be expressed explicitly. In particular,
$a_1,\ldots, a_{k-1}$
can be expressed explicitly. In particular,
Note that, for sufficiently small t,
![]() $\partial A(u,t)/\partial t=\sigma_+(t)-\sigma_-(t)$
.
$\partial A(u,t)/\partial t=\sigma_+(t)-\sigma_-(t)$
.
Now we turn to expressing the Jacobian J(u, t) in the form of a series expansion in t. Using (7) and (8), we get
 \begin{align} \ell(u,t) & = \int_{\sigma_-}^{\sigma^+}\sqrt{1+(g'_{\!\!t}(\sigma))^2}\,\textrm{d}\sigma = \int_{\sigma_-}^{\sigma^+}\sqrt{\frac{1}{1-\sigma^2}}\,\textrm{d}\sigma = \big[\arcsin\sigma\big]_{\sigma_-}^{\sigma_+} \notag \\[5pt] & = h_1t^{1/2} + h_2t + \cdots + h_{k-1}t^{({k-1})/{2}} + O(t^{{k}/{2}}), \end{align}
\begin{align} \ell(u,t) & = \int_{\sigma_-}^{\sigma^+}\sqrt{1+(g'_{\!\!t}(\sigma))^2}\,\textrm{d}\sigma = \int_{\sigma_-}^{\sigma^+}\sqrt{\frac{1}{1-\sigma^2}}\,\textrm{d}\sigma = \big[\arcsin\sigma\big]_{\sigma_-}^{\sigma_+} \notag \\[5pt] & = h_1t^{1/2} + h_2t + \cdots + h_{k-1}t^{({k-1})/{2}} + O(t^{{k}/{2}}), \end{align}
where the coefficients
![]() $h_1,\ldots, h_{k-1}$
can be expressed explicitly. In particular,
$h_1,\ldots, h_{k-1}$
can be expressed explicitly. In particular,
Note that the coefficients
![]() $c_1, c_2, c_3$
(also
$c_1, c_2, c_3$
(also
![]() $\tilde{c}_1, \tilde{c}_2, \tilde{c}_3$
),
$\tilde{c}_1, \tilde{c}_2, \tilde{c}_3$
),
![]() $a_1, a_2, a_3$
, and
$a_1, a_2, a_3$
, and
![]() $h_1, h_2, h_3$
were calculated in [Reference Fodor, Kevei and Vígh11, pp. 911–912] with a different notation.
$h_1, h_2, h_3$
were calculated in [Reference Fodor, Kevei and Vígh11, pp. 911–912] with a different notation.
Now, using (10), we get
where the coefficients
![]() $l_1,\ldots, l_{k-1}$
can be calculated explicitly. In particular,
$l_1,\ldots, l_{k-1}$
can be calculated explicitly. In particular,
Then,
where the coefficients
![]() $j_1,\ldots, j_{k-1}$
can be calculated explicitly. In particular,
$j_1,\ldots, j_{k-1}$
can be calculated explicitly. In particular,
 \begin{equation*} j_1 = \frac{8u_2^{-3/2}(\kappa-1)}{3\kappa} , \qquad j_2 = 0, \qquad j_3 = \frac{8u_2^{-3/2}}{3} + \frac{25u_3^2 + 4u_2(u_2 - 5u_4)}{5u_2^{9/2}}\frac{(\kappa-1)}{\kappa}.\end{equation*}
\begin{equation*} j_1 = \frac{8u_2^{-3/2}(\kappa-1)}{3\kappa} , \qquad j_2 = 0, \qquad j_3 = \frac{8u_2^{-3/2}}{3} + \frac{25u_3^2 + 4u_2(u_2 - 5u_4)}{5u_2^{9/2}}\frac{(\kappa-1)}{\kappa}.\end{equation*}
For a fixed n, let
![]() $y=y(u,t)$
be defined by
$y=y(u,t)$
be defined by
Then, by (9) and using Lemma 2 for
![]() $\sqrt t$
and then squaring, we obtain
$\sqrt t$
and then squaring, we obtain
where the coefficients
![]() $p_1,\ldots, p_{k-1}$
can be calculated explicitly. In particular,
$p_1,\ldots, p_{k-1}$
can be calculated explicitly. In particular,
Then, substituting (12) into (11), we obtain
where the coefficients
![]() $q_1,\ldots, q_{k-1}$
can be calculated explicitly. In particular,
$q_1,\ldots, q_{k-1}$
can be calculated explicitly. In particular,
In the coefficients
![]() $q_1, q_3$
we used
$q_1, q_3$
we used
![]() $j_1, j_3$
and
$j_1, j_3$
and
![]() $p_1, p_3$
instead of the
$p_1, p_3$
instead of the
![]() $u_i$
in order to simplify the notation.
$u_i$
in order to simplify the notation.
4. The incomplete beta function
In evaluating the integral (5), we use the following expansion of the incomplete beta function from [Reference Gruber14].
Lemma 3 ([Reference Gruber14].) Let
![]() $\beta\in\mathbb{R}$
. There are coefficients
$\beta\in\mathbb{R}$
. There are coefficients
![]() $\gamma_1, \gamma_2,\ldots\in \mathbb{R}$
depending on
$\gamma_1, \gamma_2,\ldots\in \mathbb{R}$
depending on
![]() $\beta$
that can be determined explicitly such that, for a fixed
$\beta$
that can be determined explicitly such that, for a fixed
![]() $l=1,2,\ldots$
and
$l=1,2,\ldots$
and
![]() $0<\alpha\leq 1$
,
$0<\alpha\leq 1$
,
In particular,
If
![]() $\alpha$
is chosen from a closed subinterval of (0,1], then the constant in
$\alpha$
is chosen from a closed subinterval of (0,1], then the constant in
![]() $O(\!\cdot\!)$
can be chosen independent of
$O(\!\cdot\!)$
can be chosen independent of
![]() $\alpha$
.
$\alpha$
.
In our calculations, we need the following corollary of Lemma 3.
Lemma 4. Under the assumptions of Lemma 3, there are coefficients
![]() $\gamma^{\prime}_1,\gamma^{\prime}_2,\ldots\in\mathbb{R}$
such that
$\gamma^{\prime}_1,\gamma^{\prime}_2,\ldots\in\mathbb{R}$
such that
In particular,
If
![]() $\alpha$
is chosen from a closed subinterval of (0,1], then the constant in
$\alpha$
is chosen from a closed subinterval of (0,1], then the constant in
![]() $O(\!\cdot\!)$
can be chosen independent of
$O(\!\cdot\!)$
can be chosen independent of
![]() $\alpha$
.
$\alpha$
.
Proof. Using Lemma 3 and
we obtain
 \begin{align*} & \int_{0}^{\alpha(n-2)}\bigg(1-\frac{t}{n-2}\bigg)^{n-2}t^\beta\,\textrm{d}t \\ & \quad = \Gamma(\beta+1) + \frac{\gamma_1}{n}\frac{n}{n-2} + \cdots + \frac{\gamma_l}{n^l}\frac{n^l}{(n-2)^l} + O\bigg(\frac{1}{n^{l+1}}\frac{n^{l+1}}{(n-2)^{l+1}}\bigg) \\[5pt] & \quad = \Gamma(\beta+1) + \frac{\gamma^{\prime}_{1}}{n} + \cdots + \frac{\gamma^{\prime}_{l}}{n^l} + O\bigg(\frac{1}{n^{l+1}}\bigg),\end{align*}
\begin{align*} & \int_{0}^{\alpha(n-2)}\bigg(1-\frac{t}{n-2}\bigg)^{n-2}t^\beta\,\textrm{d}t \\ & \quad = \Gamma(\beta+1) + \frac{\gamma_1}{n}\frac{n}{n-2} + \cdots + \frac{\gamma_l}{n^l}\frac{n^l}{(n-2)^l} + O\bigg(\frac{1}{n^{l+1}}\frac{n^{l+1}}{(n-2)^{l+1}}\bigg) \\[5pt] & \quad = \Gamma(\beta+1) + \frac{\gamma^{\prime}_{1}}{n} + \cdots + \frac{\gamma^{\prime}_{l}}{n^l} + O\bigg(\frac{1}{n^{l+1}}\bigg),\end{align*}
from which we can get the coefficients
![]() $\gamma^{\prime}_{1},\ldots, \gamma^{\prime}_{l}$
by simple calculation.
$\gamma^{\prime}_{1},\ldots, \gamma^{\prime}_{l}$
by simple calculation.
5. Proof of Theorem 2
Proof of Theorem 2. Substituting (13) in the integral (5) and using (12), we obtain
 \begin{align*} \mathbb{E}(f_0(K_n^1)) & = \left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac1{A^2} \int_{S^1}\int_0^{t_1}\bigg(1-\frac{A(u,t)}{A}\bigg)^{n-2}J(u,t)\,\textrm{d}t\textrm{d}u + O(n^{-k}) \\[5pt] & = \left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{1}{A^2}\frac{1}{n-2}\int_{S^1}\int_{0}^{\tau(n-2)}\bigg(1-\frac{y}{n-2}\bigg)^{n-2} J\bigg(u,\frac{y}{n-2}\bigg)t'\bigg(\frac{y}{n-2}\bigg)\,\textrm{d}y\textrm{d}u \\[5pt] &\quad + O(n^{-k}). \end{align*}
\begin{align*} \mathbb{E}(f_0(K_n^1)) & = \left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac1{A^2} \int_{S^1}\int_0^{t_1}\bigg(1-\frac{A(u,t)}{A}\bigg)^{n-2}J(u,t)\,\textrm{d}t\textrm{d}u + O(n^{-k}) \\[5pt] & = \left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{1}{A^2}\frac{1}{n-2}\int_{S^1}\int_{0}^{\tau(n-2)}\bigg(1-\frac{y}{n-2}\bigg)^{n-2} J\bigg(u,\frac{y}{n-2}\bigg)t'\bigg(\frac{y}{n-2}\bigg)\,\textrm{d}y\textrm{d}u \\[5pt] &\quad + O(n^{-k}). \end{align*}
We evaluate the inner integral as follows. Collecting the terms according to the exponent of
![]() $y/(n-2)$
and also the error term yields
$y/(n-2)$
and also the error term yields
 \begin{equation} \begin{aligned} \left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{1}{A^2} & \frac{1}{n-2}\int_{0}^{\tau(n-2)}\bigg(1-\frac{y}{n-2}\bigg)^{n-2}J\bigg(u,\frac{y}{n-2}\bigg)t' \bigg(\frac{y}{n-2}\bigg)\,\textrm{d}y \\[5pt] & = v_1\left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{1}{A^2}\frac{1}{(n-2)^{5/3}} \int_{0}^{\tau(n-2)}\bigg(1-\frac{y}{n-2}\bigg)^{n-2}y^{2/3}\,\textrm{d}y + \cdots \\[5pt] & \quad + v_{k-1}\left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{1}{A^2}\frac{1}{(n-2)^{({k+3})/{3}}} \int_{0}^{\tau(n-2)}\bigg(1-\frac{y}{n-2}\bigg)^{n-2}y^{{k}/3}\,\textrm{d}y \\[5pt] & \quad + O\bigg(\frac{1}{(n-2)^{({k-2})/3}} \int_{0}^{\tau(n-2)}\bigg(1-\frac{y}{n-2}\bigg)^{n-2}y^{({k+1})/3}\,\textrm{d}y\bigg) \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{1}{A^2} & \frac{1}{n-2}\int_{0}^{\tau(n-2)}\bigg(1-\frac{y}{n-2}\bigg)^{n-2}J\bigg(u,\frac{y}{n-2}\bigg)t' \bigg(\frac{y}{n-2}\bigg)\,\textrm{d}y \\[5pt] & = v_1\left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{1}{A^2}\frac{1}{(n-2)^{5/3}} \int_{0}^{\tau(n-2)}\bigg(1-\frac{y}{n-2}\bigg)^{n-2}y^{2/3}\,\textrm{d}y + \cdots \\[5pt] & \quad + v_{k-1}\left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{1}{A^2}\frac{1}{(n-2)^{({k+3})/{3}}} \int_{0}^{\tau(n-2)}\bigg(1-\frac{y}{n-2}\bigg)^{n-2}y^{{k}/3}\,\textrm{d}y \\[5pt] & \quad + O\bigg(\frac{1}{(n-2)^{({k-2})/3}} \int_{0}^{\tau(n-2)}\bigg(1-\frac{y}{n-2}\bigg)^{n-2}y^{({k+1})/3}\,\textrm{d}y\bigg) \end{aligned} \end{equation}
as
![]() $n\to\infty$
. The coefficients
$n\to\infty$
. The coefficients
![]() $v_1,\ldots, v_{k-1}$
can be determined explicitly. In particular,
$v_1,\ldots, v_{k-1}$
can be determined explicitly. In particular,
Here we use
![]() $p_1, p_3$
and
$p_1, p_3$
and
![]() $q_1, q_3$
to express
$q_1, q_3$
to express
![]() $v_1, v_3$
for the sake of brevity. Of course, they can also be expressed explicitly in terms of the
$v_1, v_3$
for the sake of brevity. Of course, they can also be expressed explicitly in terms of the
![]() $u_i$
.
$u_i$
.
We evaluate the above integrals one by one using Lemma 4. In particular, the first integral is as follows:
 \begin{align*} v_1\left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{1}{A^2} & \frac{1}{(n-2)^{5/3}}\int_{0}^{\tau(n-2)}\bigg(1-\frac{y}{n-2}\bigg)^{n-2}y^{2/3}\,\textrm{d}y \\[5pt] & = \sqrt[3]{\frac{2}{3A}}\frac{(\kappa-1)^{1/3}}{\kappa}\frac{n(n-1)}{(n-2)^{5/3}} \bigg(\Gamma\bigg(\frac53\bigg) - \frac{\Gamma({10}/{3})}{2}\frac{1}{n} + \cdots \bigg) \\[5pt] & = \sqrt[3]{\frac{2}{3A}}\frac{(\kappa-1)^{1/3}}{\kappa} \bigg(\Gamma\bigg(\frac53\bigg)n^{1/3} + \bigg(\frac73\Gamma\bigg(\frac{5}{3}\bigg) - \frac{\Gamma({10}/{3})}{2}\bigg)\frac{1}{n^{2/3}} + \cdots\bigg), \end{align*}
\begin{align*} v_1\left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{1}{A^2} & \frac{1}{(n-2)^{5/3}}\int_{0}^{\tau(n-2)}\bigg(1-\frac{y}{n-2}\bigg)^{n-2}y^{2/3}\,\textrm{d}y \\[5pt] & = \sqrt[3]{\frac{2}{3A}}\frac{(\kappa-1)^{1/3}}{\kappa}\frac{n(n-1)}{(n-2)^{5/3}} \bigg(\Gamma\bigg(\frac53\bigg) - \frac{\Gamma({10}/{3})}{2}\frac{1}{n} + \cdots \bigg) \\[5pt] & = \sqrt[3]{\frac{2}{3A}}\frac{(\kappa-1)^{1/3}}{\kappa} \bigg(\Gamma\bigg(\frac53\bigg)n^{1/3} + \bigg(\frac73\Gamma\bigg(\frac{5}{3}\bigg) - \frac{\Gamma({10}/{3})}{2}\bigg)\frac{1}{n^{2/3}} + \cdots\bigg), \end{align*}
where in the last line we used the binomial series expansion
The second (nonzero) integral is the following:
 \begin{align*} v_3\left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{1}{A^2} & \frac{1}{(n-2)^{7/3}}\int_{0}^{\tau(n-2)}\bigg(1-\frac{y}{n-2}\bigg)^{n-2}y^{4/3}\,\textrm{d}y \\[5pt] & = \frac{v_3}{2A^2}\frac{n(n-1)}{(n-2)^{7/3}}\bigg(\Gamma\bigg(\frac73\bigg) - \frac{\Gamma({13}/{3})}{2}\frac{1}{n} + \cdots\bigg) \\[5pt] & = \frac{v_3}{2A^2}\bigg(\Gamma\bigg(\frac73\bigg)n^{-1/3} + \bigg(\frac{11\Gamma(7/3)}{3} - \frac{\Gamma({13}/{3})}{2}\bigg)n^{-4/3} + \cdots\bigg), \end{align*}
\begin{align*} v_3\left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{1}{A^2} & \frac{1}{(n-2)^{7/3}}\int_{0}^{\tau(n-2)}\bigg(1-\frac{y}{n-2}\bigg)^{n-2}y^{4/3}\,\textrm{d}y \\[5pt] & = \frac{v_3}{2A^2}\frac{n(n-1)}{(n-2)^{7/3}}\bigg(\Gamma\bigg(\frac73\bigg) - \frac{\Gamma({13}/{3})}{2}\frac{1}{n} + \cdots\bigg) \\[5pt] & = \frac{v_3}{2A^2}\bigg(\Gamma\bigg(\frac73\bigg)n^{-1/3} + \bigg(\frac{11\Gamma(7/3)}{3} - \frac{\Gamma({13}/{3})}{2}\bigg)n^{-4/3} + \cdots\bigg), \end{align*}
where we used the binomial series expansion
Evaluating the
![]() $k-1$
integrals in (14) and collecting the terms, including the error term, we obtain
$k-1$
integrals in (14) and collecting the terms, including the error term, we obtain
 \begin{align*} \left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac1{A^2}\int_0^{t_1}\bigg(1-\frac{A(u,t)}{A}\bigg)^{n-2}J(u,t)\,\textrm{d}t &= w_1n^{1/3} + w_2n^0 + \cdots + w_{k-1}n^{-({k-3})/{3}}\\[5pt] &\quad + O(n^{-({k-2})/{3}}), \end{align*}
\begin{align*} \left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac1{A^2}\int_0^{t_1}\bigg(1-\frac{A(u,t)}{A}\bigg)^{n-2}J(u,t)\,\textrm{d}t &= w_1n^{1/3} + w_2n^0 + \cdots + w_{k-1}n^{-({k-3})/{3}}\\[5pt] &\quad + O(n^{-({k-2})/{3}}), \end{align*}
where, in principle, all the coefficients
![]() $w_1,\ldots, w_{k-1}$
can be calculated explicitly. In particular,
$w_1,\ldots, w_{k-1}$
can be calculated explicitly. In particular,
 \begin{align*} w_1(u) & = \sqrt[3]{\frac{2}{3A}}\Gamma\bigg(\frac53\bigg)\frac{(\kappa(u)-1)^{1/3}}{\kappa(u)}, \\[5pt] w_2(u) & = 0, \\[5pt] w_3(u) & = -\Gamma\bigg(\frac73\bigg)\frac{1}{5}\sqrt[3]{\frac{3A}{2}} \bigg(\frac{\kappa''(u)}{3(\kappa(u)-1)^{4/3}\kappa(u)} + \frac{2\kappa^2(u)+7\kappa(u)-1}{2(\kappa(u)-1)^{1/3}\kappa(u)} - \frac{5(\kappa'(u))^2}{9(\kappa(u)-1)^{7/3}\kappa(u)}\bigg), \end{align*}
\begin{align*} w_1(u) & = \sqrt[3]{\frac{2}{3A}}\Gamma\bigg(\frac53\bigg)\frac{(\kappa(u)-1)^{1/3}}{\kappa(u)}, \\[5pt] w_2(u) & = 0, \\[5pt] w_3(u) & = -\Gamma\bigg(\frac73\bigg)\frac{1}{5}\sqrt[3]{\frac{3A}{2}} \bigg(\frac{\kappa''(u)}{3(\kappa(u)-1)^{4/3}\kappa(u)} + \frac{2\kappa^2(u)+7\kappa(u)-1}{2(\kappa(u)-1)^{1/3}\kappa(u)} - \frac{5(\kappa'(u))^2}{9(\kappa(u)-1)^{7/3}\kappa(u)}\bigg), \end{align*}
where we recall that
![]() $\kappa$
is a function of u.
$\kappa$
is a function of u.
We note here that, when calculating further coefficients, we must also take into account some of the lower-order terms from previous integrals. This does not yet affect the evaluation of
![]() $w_3$
, as the second-largest term in the first integral is
$w_3$
, as the second-largest term in the first integral is
![]() $n^{-2/3}$
. However, this would have to be added when calculating
$n^{-2/3}$
. However, this would have to be added when calculating
![]() $w_4$
, and so on.
$w_4$
, and so on.
Finally, integration with respect to u yields
 \begin{align*} \mathbb{E}(f_0(K_n^1)) & = \int_{S^1}w_1(u)n^{1/3} + w_2(u)n^0 + \cdots + w_{k-1}(u)n^{-({k-3})/{3}} + O(n^{-({k-2})/{3}})\,\textrm{d}u \\[5pt] & = z_1(K)n^{1/3} + z_2(K)n^0 + \cdots + z_{k-1}(K)n^{-({k-3})/{3}} + O(n^{-({k-2})/{3}}), \end{align*}
\begin{align*} \mathbb{E}(f_0(K_n^1)) & = \int_{S^1}w_1(u)n^{1/3} + w_2(u)n^0 + \cdots + w_{k-1}(u)n^{-({k-3})/{3}} + O(n^{-({k-2})/{3}})\,\textrm{d}u \\[5pt] & = z_1(K)n^{1/3} + z_2(K)n^0 + \cdots + z_{k-1}(K)n^{-({k-3})/{3}} + O(n^{-({k-2})/{3}}), \end{align*}
where, again, all coefficient can be found explicitly. In particular,
 \begin{align*} z_1(K) & = \int_{S^1}w_1(u)\,\textrm{d}u = \sqrt[3]{\frac{2}{3A}}\Gamma\bigg(\frac53\bigg) \int_{\partial K}(\kappa(x)-1)^{1/3}\,\textrm{d}x, \\[5pt] z_2(K) & = 0, \\[5pt] z_3(K) & = \int_{S^1}w_3(u)\,\textrm{d}u \\[5pt] & = -\Gamma\bigg(\frac73\bigg)\frac{1}{5}\sqrt[3]{\frac{3A}{2}} \int_{\partial K}\frac{\kappa''(x)}{3(\kappa(x)-1)^{4/3}} + \frac{2\kappa(x)^2+7\kappa(x)-1}{2(\kappa(x)-1)^{1/3}} - \frac{5(\kappa'(x))^2}{9(\kappa(x)-1)^{7/3}}\,\textrm{d}x, \end{align*}
\begin{align*} z_1(K) & = \int_{S^1}w_1(u)\,\textrm{d}u = \sqrt[3]{\frac{2}{3A}}\Gamma\bigg(\frac53\bigg) \int_{\partial K}(\kappa(x)-1)^{1/3}\,\textrm{d}x, \\[5pt] z_2(K) & = 0, \\[5pt] z_3(K) & = \int_{S^1}w_3(u)\,\textrm{d}u \\[5pt] & = -\Gamma\bigg(\frac73\bigg)\frac{1}{5}\sqrt[3]{\frac{3A}{2}} \int_{\partial K}\frac{\kappa''(x)}{3(\kappa(x)-1)^{4/3}} + \frac{2\kappa(x)^2+7\kappa(x)-1}{2(\kappa(x)-1)^{1/3}} - \frac{5(\kappa'(x))^2}{9(\kappa(x)-1)^{7/3}}\,\textrm{d}x, \end{align*}
where we use that if
![]() $\partial K$
is
$\partial K$
is
![]() $C^2_+$
-smooth and f(u) is a measurable function on
$C^2_+$
-smooth and f(u) is a measurable function on
![]() $S^1$
, then
$S^1$
, then
![]() $\int_{S^1}f(u)\,\textrm{d}u = \int_{\partial K}f(u_x)\kappa(x)\,\textrm{d}x$
[Reference Schneider30, (2.62)]. This completes the proof of Theorem 2.
$\int_{S^1}f(u)\,\textrm{d}u = \int_{\partial K}f(u_x)\kappa(x)\,\textrm{d}x$
[Reference Schneider30, (2.62)]. This completes the proof of Theorem 2.
6. The case of the unit circle
For the sake of completeness, we consider the case when
![]() $K=B(R)$
. Since
$K=B(R)$
. Since
![]() $\mathbb{E}(f_0(B(R)_n^R))$
is independent of R, we may assume that
$\mathbb{E}(f_0(B(R)_n^R))$
is independent of R, we may assume that
![]() $R=1$
. We will use the simpler notation
$R=1$
. We will use the simpler notation
![]() $B_n^1=B(1)_n^1$
. In [Reference Fodor, Kevei and Vígh11, p. 916] it was proved that
$B_n^1=B(1)_n^1$
. In [Reference Fodor, Kevei and Vígh11, p. 916] it was proved that
Let
Since
![]() $\sin(\sigma)+\sigma$
is a strictly monotonically increasing analytic function on
$\sin(\sigma)+\sigma$
is a strictly monotonically increasing analytic function on
![]() $[0,\pi]$
, its inverse is also a strictly monotonically increasing analytic function by the Lagrange inversion theorem. Then
$[0,\pi]$
, its inverse is also a strictly monotonically increasing analytic function by the Lagrange inversion theorem. Then
![]() $\sigma$
has a power-series expansion in terms of
$\sigma$
has a power-series expansion in terms of
![]() $y/(n-1)$
around
$y/(n-1)$
around
![]() $y=0$
as follows:
$y=0$
as follows:
where all the coefficients can be calculated explicitly. In particular,
Thus,
where the coefficients can be calculated explicitly. In particular,
Therefore,
 \begin{align*} \mathbb{E}(f_0(B^1_n)) & = \left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{4}{n-1}\int_0^{n-1}\bigg(1-\frac{y}{n-1}\bigg)^{n-1} \sin\bigg(\sigma\bigg(\frac{y}{n-1}\bigg)\bigg)\sigma'\bigg(\frac{y}{n-1}\bigg)\,\textrm{d}y \\[5pt] & = f_1\left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{4}{(n-1)^2}\int_0^{n-1}\bigg(1-\frac{y}{n-1}\bigg)^{n-1}y\,\textrm{d}y \\[5pt] & \quad + f_3\left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{4}{(n-1)^4}\int_0^{n-1}\bigg(1-\frac{y}{n-1}\bigg)^{n-1}y^3\,\textrm{d}y \\[5pt] & \quad + \cdots + f_{2k+1}\left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{4}{(n-1)^{2k+2}} \int_0^{n-1}\bigg(1-\frac{y}{n-1}\bigg)^{n-1}y^{2k+1}\,\textrm{d}y + \cdots,\end{align*}
\begin{align*} \mathbb{E}(f_0(B^1_n)) & = \left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{4}{n-1}\int_0^{n-1}\bigg(1-\frac{y}{n-1}\bigg)^{n-1} \sin\bigg(\sigma\bigg(\frac{y}{n-1}\bigg)\bigg)\sigma'\bigg(\frac{y}{n-1}\bigg)\,\textrm{d}y \\[5pt] & = f_1\left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{4}{(n-1)^2}\int_0^{n-1}\bigg(1-\frac{y}{n-1}\bigg)^{n-1}y\,\textrm{d}y \\[5pt] & \quad + f_3\left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{4}{(n-1)^4}\int_0^{n-1}\bigg(1-\frac{y}{n-1}\bigg)^{n-1}y^3\,\textrm{d}y \\[5pt] & \quad + \cdots + f_{2k+1}\left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{4}{(n-1)^{2k+2}} \int_0^{n-1}\bigg(1-\frac{y}{n-1}\bigg)^{n-1}y^{2k+1}\,\textrm{d}y + \cdots,\end{align*}
where all the coefficients
![]() $f_1,\ldots, f_{2k+1},\ldots$
can be evaluated explicitly using Lemma 3 and the binomial series expansion of
$f_1,\ldots, f_{2k+1},\ldots$
can be evaluated explicitly using Lemma 3 and the binomial series expansion of
![]() $n/(n-1)^{2k+1}$
. In particular,
$n/(n-1)^{2k+1}$
. In particular,
Thus, by Lemma 4, the first integral yields
 \begin{align*} \left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{\pi^2}{(n-1)^2} & \int_0^{n-1}\bigg(1-\frac{y}{n-1}\bigg)^{n-1}y\,\textrm{d} y \\[5pt] & = \frac{\pi^2}{2}\frac{n}{n-1}\bigg(\Gamma(2) - \frac{\Gamma(4)}{2}\frac{1}{n-1} + \bigg(\frac{-\Gamma(5)}{3} + \frac{\Gamma(6)}{8}\bigg)\frac{1}{(n-1)^2} + \cdots\bigg) \\[5pt] & = \frac{\pi^2}{2}\bigg(1-\frac{2}{n} + \frac{2}{n^2} + \cdots\bigg)\end{align*}
\begin{align*} \left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{\pi^2}{(n-1)^2} & \int_0^{n-1}\bigg(1-\frac{y}{n-1}\bigg)^{n-1}y\,\textrm{d} y \\[5pt] & = \frac{\pi^2}{2}\frac{n}{n-1}\bigg(\Gamma(2) - \frac{\Gamma(4)}{2}\frac{1}{n-1} + \bigg(\frac{-\Gamma(5)}{3} + \frac{\Gamma(6)}{8}\bigg)\frac{1}{(n-1)^2} + \cdots\bigg) \\[5pt] & = \frac{\pi^2}{2}\bigg(1-\frac{2}{n} + \frac{2}{n^2} + \cdots\bigg)\end{align*}
The second integral yields
 \begin{align*} f_3\left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{4}{(n-1)^4} & \int_0^{n-1}\bigg(1-\frac{y}{n-1}\bigg)^{n-1}y^3\,\textrm{d}y \\[5pt] & = \frac{\pi^4}{48}\frac{n}{(n-1)^3}\bigg(\Gamma(4) - \frac{\Gamma(6)}{3}\frac{1}{n-1} + \bigg({-}\frac{\Gamma(7)}{3} + \frac{\Gamma(8)}{8}\bigg)\frac{1}{(n-1)^2} + \cdots\bigg)\end{align*}
\begin{align*} f_3\left(\begin{array}{c}{n}\\[2pt] {2}\end{array}\right)\frac{4}{(n-1)^4} & \int_0^{n-1}\bigg(1-\frac{y}{n-1}\bigg)^{n-1}y^3\,\textrm{d}y \\[5pt] & = \frac{\pi^4}{48}\frac{n}{(n-1)^3}\bigg(\Gamma(4) - \frac{\Gamma(6)}{3}\frac{1}{n-1} + \bigg({-}\frac{\Gamma(7)}{3} + \frac{\Gamma(8)}{8}\bigg)\frac{1}{(n-1)^2} + \cdots\bigg)\end{align*}
Thus, for any k,
![]() $\mathbb{E}(f_0(B^1_n)) = w_0 n^{0}+w_1n^{-1}+w_2n^{-2}+\cdots+w_k n^{-k}+O(n^{-k-1})$
, where all the coefficients
$\mathbb{E}(f_0(B^1_n)) = w_0 n^{0}+w_1n^{-1}+w_2n^{-2}+\cdots+w_k n^{-k}+O(n^{-k-1})$
, where all the coefficients
![]() $w_1,\ldots w_1,\ldots,w_k$
can be calculated explicitly. In particular,
$w_1,\ldots w_1,\ldots,w_k$
can be calculated explicitly. In particular,
Acknowledgements
The authors are grateful to Viktor Vígh for helpful discussions, and to the anonymous referees for valuable suggestions that greatly improved the presentation of the paper.
Funding information
F. Fodor was supported by the Hungarian National Research, Development and Innovation Office – NKFIH K134814 grant.
This research was supported by project TKP2021-NVA-09. Project no. TKP2021-NVA-09 has been implemented with support provided by the Ministry of Culture and Innovation of Hungary from the National Research, Development and Innovation Fund, financed under the TKP2021-NVA funding scheme.
Supported by University of Szeged Open Access Fund, Grant Number 6829.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.