Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T18:26:40.515Z Has data issue: false hasContentIssue false
  • English
  • Français

Sensitivity of mean-field fluctuations in Erlang loss models with randomized routing

Part of: Limit theorems Special processes Computer system organization

Published online by Cambridge University Press:  23 June 2021

Thirupathaiah Vasantam  and
Ravi R. Mazumdar Open the ORCID record for Ravi R. Mazumdar [Opens in a new window]
Thirupathaiah Vasantam*
Affiliation:
University of Massachusetts, Amherst
Ravi R. Mazumdar*
Affiliation:
University of Waterloo
*
*Postal address: College of Information and Computer Sciences, Amherst, MA 01003, USA. E-mail address: [email protected]
**Postal address: Department of Electrical and Computer Engineering, 200 University Ave W, Waterloo, ON N2L 3G1, Canada. E-mail address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study a large system of N servers, each with capacity to process at most C simultaneous jobs; an incoming job is routed to a server if it has the lowest occupancy amongst d (out of N) randomly selected servers. A job that is routed to a server with no vacancy is assumed to be blocked and lost. Such randomized policies are referred to JSQ(d) (Join the Shortest Queue out of d) policies. Under the assumption that jobs arrive according to a Poisson process with rate 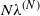$N\lambda^{(N)}$ where 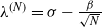$\lambda^{(N)}=\sigma-\frac{\beta}{\sqrt{N}\,}$ , 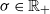$\sigma\in\mathbb{R}_+$ and 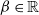$\beta\in\mathbb{R}$ , we establish functional central limit theorems for the fluctuation process in both the transient and stationary regimes when service time distributions are exponential. In particular, we show that the limit is an Ornstein–Uhlenbeck process whose mean and variance depend on the mean field of the considered model. Using this, we obtain approximations to the blocking probabilities for large N, where we can precisely estimate the accuracy of first-order approximations.

Keywords

Loss modelsJSQ(d)Halfin–Whitt regimefunctional central limit theoremsfluctuationsmean field

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Secondary: 60F17: Functional limit theorems; invariance principles 68M20: Performance evaluation; queueing; scheduling
Type
Original Article
Information
Journal of Applied Probability , Volume 58 , Issue 2 , June 2021 , pp. 428 - 448
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amazon EC2. (2021) http://aws.amazon.com/ec2/.Google Scholar
Asmussen, S. (2003). Applied Probability and Queues. Springer, New York.Google Scholar
Eschenfeldt, P. and Gamarnik, D. (2018). Join the shortest queue with many servers. The heavy-traffic asymptotics. Math. Operat. Res. 43, 867–886.Google Scholar
Ethier, S. N. and Kurtz, T. G. (1985). Markov Processes: Characterization and Convergence. John Wiley, New York.Google Scholar
Gast, N. (2017). Expected values estimated via mean-field approximation are $1/N$ -accurate. Proc. ACM Meas. Anal. Comput. Sys. 1, 17.Google Scholar
Gast, N. and Van Houdt, B. (2017). A refined mean field approximation. Proc. ACM Meas. Anal. Comput. Sys. 1, 33.10.1145/3154491CrossRefGoogle Scholar
Gazdzicki, P., Lambadaris, I. and Mazumdar, R. (1993). Blocking probabilities for large multi-rate Erlang loss systems. Adv. Appl. Prob. 25, 997–1009.10.2307/1427803CrossRefGoogle Scholar
Graham, C. (2000). Chaoticity on path space for a queueing network with selection of the shortest queue among several. J. Appl. Prob. 37, 198–211.10.1239/jap/1014842277CrossRefGoogle Scholar
Graham, C. (2005). Functional central limit theorems for a large network in which customers join the shortest of several queues. Prob. Theory Relat. Fields 131, 97–120.10.1007/s00440-004-0372-9CrossRefGoogle Scholar
Karthik, A., Mukhopadhyay, A. and Mazumdar, R. R. (2017). Choosing among heterogeneous server clouds. Queueing Systems 85, 1–29.10.1007/s11134-016-9488-8CrossRefGoogle Scholar
Ledermann, W., Reuter, G. E. H. and Mahler, K. (1954). Spectral theory for the differential equations of simple birth and death processes. Phil. Trans. R. Soc. London A 246, 321–369.Google Scholar
Microsoft, Azure. (2021) http://www.microsoft.com/windowsazure/.Google Scholar
Mitzenmacher, M. (1996). The power of two choices in randomized load balancing. PhD thesis, University of California, Berkeley.Google Scholar
Mukherjee, D., Borst, S. C., van Leeuwaarden, J. and Whiting, P. A. (2016). Asymptotic optimality of power-of-$d$ load balancing in large-scale systems. Preprint, .Google Scholar
Mukhopadhyay, A., Mazumdar, R. R. and Guillemin, F. (2015). The power of randomized routing in heterogeneous loss systems. In Proc. 27th Int. Teletraffic Congress, pp. 125–133.10.1109/ITC.2015.22CrossRefGoogle Scholar
Mukhopadhyay, A., Karthik, A., Mazumdar, R. R. and Guillemin, F. M. (2015). Mean field and propagation of chaos in multi-class heterogeneous loss models. Performance Evaluation 91, 117–131.10.1016/j.peva.2015.06.008CrossRefGoogle Scholar
Pang, G., Talreja, R. and Whitt, W. (2007). Martingale proofs of many-server heavy-traffic limits for Markovian queues. Prob. Surv. 4, 193–267.10.1214/06-PS091CrossRefGoogle Scholar
Vasantam, T. and Mazumdar, R. R. (2018) On occupancy based randomized routing schemes in large systems of shared servers. In Proc. 30th Int. Teletraffic Congress, pp. 28–36.10.1109/ITC30.2018.00013CrossRefGoogle Scholar
Vasantam, T. and Mazumdar, R. R. (2019). Fluctuations around the mean-field for a large scale Erlang loss system under the SQ(d) load balancing. In Proc. 31st Int. Teletraffic Congress, pp. 1–9.10.1109/ITC31.2019.00010CrossRefGoogle Scholar
Vvedenskaya, N. D., Dobrushin, R. L. and Karpelevich, F. I. (1996). Queueing system with selection of the shortest of two queues: an asymptotic approach. Probl. Inform. Transm. 32, 20–34.Google Scholar
Whitt, W. (1984). Heavy-traffic approximations for service systems with blocking. AT&T Bell Lab. Tech. J. 63, 689–708.10.1002/j.1538-7305.1984.tb00102.xCrossRefGoogle Scholar
Xie, Q., Dong, X., Lu, Y. and Srikant, R. (2015). Power of d choices for large-scale bin packing: a loss model. In Proc. 2015 ACM SIGMETRICS, pp. 321–334.Google Scholar
Ying, L. (2016). On the approximation error of mean-field models. In Proc. 2016 ACM SIGMETRICS, pp. 285–297.10.1145/2896377.2901463CrossRefGoogle Scholar