Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Koutras, M. V.
1996.
On a waiting time distribution in a sequence of Bernoulli trials.
Annals of the Institute of Statistical Mathematics,
Vol. 48,
Issue. 4,
p.
789.
Kolev, Nikolai
and
Minkova, Leda
1997.
Discrete distributions related to success runs of lengthk in aulti-state markov chain.
Communications in Statistics - Theory and Methods,
Vol. 26,
Issue. 4,
p.
1031.
Koutras, Markos V.
1997.
Advances in Combinatorial Methods and Applications to Probability and Statistics.
p.
363.
Koutras, M.V.
1997.
Consecutive-k, r-out-of-n:DFM systems.
Microelectronics Reliability,
Vol. 37,
Issue. 4,
p.
597.
Koutras, M. V.
and
Alexandrou, V. A.
1997.
Sooner waiting time problems in a sequence of trinary trials.
Journal of Applied Probability,
Vol. 34,
Issue. 03,
p.
593.
Chen, Jie
and
Glaz, Joseph
1999.
Approximations for discrete scan statistics on the circle.
Statistics & Probability Letters,
Vol. 44,
Issue. 2,
p.
167.
Chadjiconstantinidis, Stathis
and
Koutras, Markos V.
1999.
Measures of component importance for markov chain imbeddable reliability structures.
Naval Research Logistics,
Vol. 46,
Issue. 6,
p.
613.
Balakrishnan, Narayanaswamy
and
Koutras, Markos V.
2000.
Random Combinations with Bounded Differences and Cospan.
The Fibonacci Quarterly,
Vol. 38,
Issue. 2,
p.
145.
2001.
Runs and Scans with Applications.
p.
389.
Koutras, M.V.
2003.
Stochastic Processes: Modelling and Simulation.
Vol. 21,
Issue. ,
p.
431.
Inoue, Kiyoshi
and
Aki, Sigeo
2003.
Generalized binomial and negative binomial distributions of orderk by thel-overlapping enumeration scheme.
Annals of the Institute of Statistical Mathematics,
Vol. 55,
Issue. 1,
p.
153.
Gani, J.
2003.
Stochastic Processes: Modelling and Simulation.
Vol. 21,
Issue. ,
p.
227.
Makri, Frosso S.
and
Philippou, Andreas N.
2005.
On binomial and circular binomial distributions of orderk forl-overlapping success runs of lengthk.
Statistical Papers,
Vol. 46,
Issue. 3,
p.
411.
Inoue, Kiyoshi
and
Aki, Sigeo
2005.
Joint distributions of numbers of success runs of specified lengths in linear and circular sequences.
Annals of the Institute of Statistical Mathematics,
Vol. 57,
Issue. 2,
p.
353.
GHORAF, NAMIR
2007.
r-CONSECUTIVE-k-OUT-OF-n: F SYSTEMS WITH DEPENDENT COMPONENTS.
International Journal of Reliability, Quality and Safety Engineering,
Vol. 14,
Issue. 04,
p.
399.
Makri, Frosso S.
Philippou, Andreas N.
and
Psillakis, Zaharias M.
2007.
Shortest and longest length of success runs in binary sequences.
Journal of Statistical Planning and Inference,
Vol. 137,
Issue. 7,
p.
2226.
Makri, Frosso S.
Philippou, Andreas N.
and
Psillakis, Zaharias M.
2007.
Success run statistics defined on an urn model.
Advances in Applied Probability,
Vol. 39,
Issue. 4,
p.
991.
Glaz, Joseph
2007.
Encyclopedia of Statistics in Quality and Reliability.
Inoue, Kiyoshi
and
Aki, Sigeo
2010.
On the conditional and unconditional distributions of the number of success runs on a circle with applications.
Statistics & Probability Letters,
Vol. 80,
Issue. 9-10,
p.
874.
Makri, Frosso S.
2010.
On Occurrences of F-S Strings in Linearly and Circularly Ordered Binary Sequences.
Journal of Applied Probability,
Vol. 47,
Issue. 01,
p.
157.


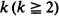 in a sequence of (not necessarily identical) Bernoulli trials arranged on a circle. An exact formula is given for the probability function, along with some sharp bounds which turn out to be very useful in establishing limiting (Poisson convergence) results. Certain applications to statistical run tests and reliability theory are also discussed.
in a sequence of (not necessarily identical) Bernoulli trials arranged on a circle. An exact formula is given for the probability function, along with some sharp bounds which turn out to be very useful in establishing limiting (Poisson convergence) results. Certain applications to statistical run tests and reliability theory are also discussed.