Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Spåtaru, Aurel
1991.
A maximum sequence in a critical multitype branching process.
Journal of Applied Probability,
Vol. 28,
Issue. 04,
p.
893.
Vatutin, V. A.
and
Zubkov, A. M.
1993.
Branching processes. II.
Journal of Soviet Mathematics,
Vol. 67,
Issue. 6,
p.
3407.
Borovkov, K. A.
and
Vatutin, V A.
1996.
On distribution tails and expectations of maxima in critical branching processes.
Journal of Applied Probability,
Vol. 33,
Issue. 03,
p.
614.
Pakes, Anthony G.
1998.
A limit theorem for the maxima of the para-critical simple branching process.
Advances in Applied Probability,
Vol. 30,
Issue. 3,
p.
740.
Rahimov, I.
2004.
Limit Theorems for the Size of Subpopulation of Productive Individuals.
Stochastic Models,
Vol. 20,
Issue. 3,
p.
261.
Ватутин, Владимир Алексеевич
Vatutin, Vladimir Alekseevich
Вахтель, Виталий Иванович
Vakhtel', Vitalii Ivanovich
Фляйшманн, К
and
Fleischmann, Klaus
2007.
Критические процессы Гальтона - Ватсона: Максимум общего числа частиц внутри большого окна.
Теория вероятностей и ее применения,
Vol. 52,
Issue. 3,
p.
419.
Vatutin, V. A.
Wachtel, V.
and
Fleischmann, K.
2008.
Critical Galton–Watson Processes: The Maximum of Total Progenies within a Large Window.
Theory of Probability & Its Applications,
Vol. 52,
Issue. 3,
p.
470.
Iksanov, Alex
and
Marynych, Alex
2008.
A note on non-regular martingales.
Statistics & Probability Letters,
Vol. 78,
Issue. 17,
p.
3014.
Wang, Xue-jun
Hu, Shu-he
Yang, Wen-zhi
and
Shen, Yan
2011.
Some new results for demimartingales.
Applied Mathematics-A Journal of Chinese Universities,
Vol. 26,
Issue. 1,
p.
14.
Hautphenne, Sophie
2015.
A Structured Markov Chain Approach to Branching Processes.
Stochastic Models,
Vol. 31,
Issue. 3,
p.
403.


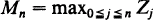 where {
where {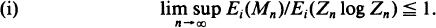
 is slowly varying at∞, conditions are given ensuring that
is slowly varying at∞, conditions are given ensuring that

