Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Baxter, Laurence A.
and
Lee, Seung Min
1989.
Further Properties of Reliability Importance for Continuum Structure Functions.
Probability in the Engineering and Informational Sciences,
Vol. 3,
Issue. 2,
p.
237.
Ryabinin, I.A.
1994.
A suggestion of a new measure of system components importance by means of a Boolean difference.
Microelectronics Reliability,
Vol. 34,
Issue. 4,
p.
603.
Zio, Enrico
and
Podofillini, Luca
2003.
Importance Measures of Multi-State Components in Multi-State Systems.
International Journal of Reliability, Quality and Safety Engineering,
Vol. 10,
Issue. 03,
p.
289.
Zio, Enrico
and
Podofillini, Luca
2003.
Monte Carlo simulation analysis of the effects of different system performance levels on the importance of multi-state components.
Reliability Engineering & System Safety,
Vol. 82,
Issue. 1,
p.
63.
Levitin, Gregory
Podofillini, Luca
and
Zio, Enrico
2003.
Generalised importance measures for multi-state elements based on performance level restrictions.
Reliability Engineering & System Safety,
Vol. 82,
Issue. 3,
p.
287.
Zio, Enrico
Podofillini, Luca
and
Levitin, Gregory
2004.
Estimation of the importance measures of multi-state elements by Monte Carlo simulation.
Reliability Engineering & System Safety,
Vol. 86,
Issue. 3,
p.
191.
Shrestha, Akhilesh
Xing, Liudong
and
Coit, David W.
2009.
Multi-state component importance analysis using multi-state multi-valued decision diagrams.
p.
99.
Shrestha, Akhilesh
Xing, Liudong
and
Coit, David W.
2010.
An Efficient Multistate Multivalued Decision Diagram-Based Approach for Multistate System Sensitivity Analysis.
IEEE Transactions on Reliability,
Vol. 59,
Issue. 3,
p.
581.
Zio, Enrico
2011.
Safety and Risk Modeling and Its Applications.
p.
151.
2012.
Importance Measures in Reliability, Risk, and Optimization.
p.
419.
Si, Shubin
Dui, Hongyan
Zhao, Xibin
Zhang, Shenggui
and
Sun, Shudong
2012.
Integrated Importance Measure of Component States Based on Loss of System Performance.
IEEE Transactions on Reliability,
Vol. 61,
Issue. 1,
p.
192.
2012.
Importance Measures in Reliability, Risk, and Optimization.
p.
297.
Way Kuo
and
Xiaoyan Zhu
2012.
Relations and Generalizations of Importance Measures in Reliability.
IEEE Transactions on Reliability,
Vol. 61,
Issue. 3,
p.
659.
Si, Shubin
Zhao, Jiangbin
Cai, Zhiqiang
and
Dui, Hongyan
2020.
Recent advances in system reliability optimization driven by importance measures.
Frontiers of Engineering Management,
Vol. 7,
Issue. 3,
p.
335.
Dui, Hongyan
Wu, Shaomin
and
Zhao, Jiangbin
2021.
Some extensions of the component maintenance priority.
Reliability Engineering & System Safety,
Vol. 214,
Issue. ,
p.
107729.
Li, Ruiying
and
Gao, Ying
2022.
On the component resilience importance measures for infrastructure systems.
International Journal of Critical Infrastructure Protection,
Vol. 36,
Issue. ,
p.
100481.
Aven, Terje
Rios Insua, David
Soyer, Refik
Zhu, Xiaoyan
and
Zio, Enrico
2024.
Fifty years of reliability in operations research.
European Journal of Operational Research,
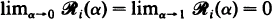 and conditions under which ℛi(α) is positive (0 < α < 1).
and conditions under which ℛi(α) is positive (0 < α < 1).