Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-25T20:15:43.761Z Has data issue: false hasContentIssue false
  • English
  • Français

Rate of convergence for traditional Pólya urns

Part of: Markov processes Limit theorems Combinatorial probability

Published online by Cambridge University Press:  23 November 2020

Svante Janson Open the ORCID record for Svante Janson [Opens in a new window]
Svante Janson*
Affiliation:
Uppsala University
*
*Postal address: Department of Mathematics, Uppsala University, PO Box 480, SE-751 06 Uppsala, Sweden. [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider a Pólya urn with balls of several colours, where balls are drawn sequentially and each drawn ball is immediately replaced together with a fixed number of balls of the same colour. It is well known that the proportions of balls of the different colours converge in distribution to a Dirichlet distribution. We show that the rate of convergence is 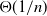$\Theta(1/n)$ in the minimal 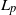$L_p$ metric for any 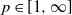$p\in[1,\infty]$, extending a result by Goldstein and Reinert; we further show the same rate for the Lévy distance, while the rate for the Kolmogorov distance depends on the parameters, i.e. on the initial composition of the urn. The method used here differs from the one used by Goldstein and Reinert, and uses direct calculations based on the known exact distributions.

Keywords

Pólya urnsDirichlet distributionconvergence rateWasserstein distanceminimal Lp distanceKolmogorov–Smirnov distanceLévy distance

MSC classification

Primary: 60C05: Combinatorial probability
Secondary: 60F05: Central limit and other weak theorems 60J99: None of the above, but in this section
Type
Research Papers
Information
Journal of Applied Probability , Volume 57 , Issue 4 , December 2020 , pp. 1029 - 1044
Check for updates
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blackwell, D. and Kendall, D. (1964). The Martin boundary of Pólya’s urn scheme, and an application to stochastic population growth. J. Appl. Prob. 1, 284–296.10.1017/S002190020010840XCrossRefGoogle Scholar
Eggenberger, F. and Pólya, G., G. (1923). Über die Statistik verketteter Vorgänge. Z. Angew. Math. Mech. 3, 279–289.10.1002/zamm.19230030407CrossRefGoogle Scholar
Freedman, D. A. (1965). Bernard Friedman’s urn. Ann. Math. Statist. 36, 956–970.10.1214/aoms/1177700068CrossRefGoogle Scholar
Gan, H. L., Röllin, A. and Ross, N. (2017). Dirichlet approximation of equilibrium distributions in Cannings models with mutation. Adv. Appl. Prob. 49, 927–959.10.1017/apr.2017.27CrossRefGoogle Scholar
Goldstein, L. and Reinert, G. (2013). Stein’s method for the beta distribution and the Pólya–Eggenberger urn. J. Appl. Prob. 50, 1187–1205.10.1017/S0021900200013875CrossRefGoogle Scholar
Janson, S. (2004). Functional limit theorems for multitype branching processes and generalized Pólya urns. Stoch. Process. Appl. 110, 177–245.10.1016/j.spa.2003.12.002CrossRefGoogle Scholar
Johnson, N. L. and Kotz, S. (1977). Urn Models and Their Application. John Wiley, New York.Google Scholar
Kallenberg, O. (2002). Foundations of Modern Probability, 2nd edn. Springer, New York.10.1007/978-1-4757-4015-8CrossRefGoogle Scholar
Kuntschik, A. and Neininger, R. (2017). Rates of convergence for balanced irreducible two-color Pólya urns. In 2017 Proceedings of the Fourteenth Workshop on Analytic Algorithmics and Combinatorics (ANALCO), pp. 94–99. SIAM, Philadelphia, PA.10.1137/1.9781611974775.9CrossRefGoogle Scholar
Mahmoud, H. M. (2009). Pólya Urn Models. CRC Press, Boca Raton, FL.Google Scholar
Markov, A. A. (1917). Sur quelques formules limites du calcul des probabilités (Russian). Bulletin de l’Académie Impériale des Sciences 11, 177–186.Google Scholar
Olver, F. W. J., Lozier, D. W., Boisvert, R. F. and Clark, C. W. (eds) (2010). NIST Handbook of Mathematical Functions, Cambridge University Press. Also available as NIST Digital Library of Mathematical Functions, http://dlmf.nist.gov/.Google Scholar
Peköz, E., Röllin, A. and Ross, N. (2016). Generalized gamma approximation with rates for urns, walks and trees. Ann. Prob. 44, 1776–1816.10.1214/15-AOP1010CrossRefGoogle Scholar
Peköz, E., Röllin, A. and Ross, N. (2017). Joint degree distributions of preferential attachment random graphs. Adv. Appl. Prob. 49, 368–387.10.1017/apr.2017.5CrossRefGoogle Scholar
Pólya, G. (1930). Sur quelques points de la théorie des probabilités. Ann. Inst. H. Poincaré 1, 117–161.Google Scholar
Rachev, S. T., Klebanov, L. B., Stoyanov, S. V. and Fabozzi, F. J. (2013). The Methods of Distances in the Theory of Probability and Statistics. Springer, New York.Google Scholar
Rüschendorf, L. Wasserstein metric. Encyclopedia of Mathematics. Available at https://www.encyclopediaofmath.org/index.php?title=Wasserstein_metric.Google Scholar
Sawyer, S. A. (1997). Martin boundaries and random walks. Harmonic Functions on Trees and Buildings (New York, 1995) (Contemp. Math. 206), pp. 17–44. American Mathematical Society, Providence, RI.Google Scholar