Let p denote the class of all probability measures defined on the Borel subsets of the unit interval I = [0, 1]. For each positive integer n, take Mn is convex, closed, bounded, and n-dimensional; the convex hull of the space curve {(t,t2, …, tn): 0 ≦ t ≦ 1}; e.g., see Theorems 7.2, 7.3 of [1]. At each point (c1, C2, …, cn) of Mn, define 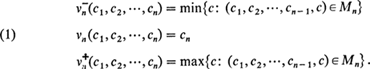Note that v−, v+ depend only on C1, C2, …, Cn− 1; Vm only on cn; We shall as notational convenience dictates and as will be apparent from the context regard v±n as functions on Mn− 1 or on higher order moment spaces and also regard Vn as a function on moment spaces of order higher than n.