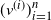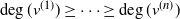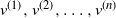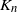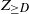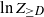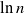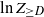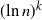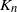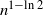1. Introduction
The idea of cutting random labeled trees was first introduced by Meir and Moon in 1970 and, soon after, they considered random recursive trees (abbreviated as RRTs) [Reference Meir and Moon42, Reference Meir and Moon43]. The original cutting procedure, for a given tree, is as follows. Start with a tree with n vertices. Choose an edge uniformly at random and remove it, along with the cut subtree that does not contain the root. Repeat until the remaining tree consists of only the root; at this point, we say that the tree has been deleted.
Random recursive trees are rooted trees, where each vertex has a unique label, obtained by the following procedure: Let 
$T_1$ be a single vertex labeled 1. For 
$n>1$ the tree 
$T_n$ is obtained from the tree 
$T_{n-1}$ by adding an edge directed from a new vertex labeled n to a vertex with label in 
$\{1,\ldots,n-1\}$, chosen uniformly at random and independent for each n. We say that 
$T_n$ has size n and that the degree of a vertex v is the number of edges directed towards v.
In this paper, we introduce a targeted vertex-cutting procedure for random recursive trees that focuses on high-degree vertices (defined in Section 1.3). Our interest in this procedure stems from the fact that it drastically reduces the number of cuts needed to destroy an RRT compared to random cuts (see Proposition 1.1), while this model may serve as a proxy for malicious attacks.
In the case of RRTs, the currently known properties of the structure of high-degree vertices do not hold to the distinct strategies previously used for studying the cutting of random trees. See [Reference Baur and Bertoin6] for a thorough survey on cutting procedures and other related processes on random recursive trees up to 2014. We give a brief overview of these and more recent models of cutting processes in Section 1.2.
To circumvent these difficulties, the core of the paper is drawn towards exploiting our knowledge on the number of high-degree vertices in RRTs. In Section 1.1, we present our main results, together with a brief description of their proof strategies. In Sections 1.2 and 1.3, we give an overview of previous cutting models and define the targeted cutting model; we also discuss in more detail the difficulties in studying the targeted cutting of RRTs and examine the implications of Theorem 1.1 on the targeted cutting process. In a nutshell, Proposition 1.1 supports the heuristic that malicious attacks may hold a strategy to take better advantage of some characteristics of the network. That is, the number of cuts required is significantly fewer than in a completely random attack. The proofs of the main results, Theorems 1.1 and 1.2, are presented in Sections 2 and 3, respectively. We close with simulations and further avenues of research in Sections 4 and 5, respectively.
1.1. Main results
For 
$d\in \mathbb{N}$, we let 
$Z_d$ and 
$Z_{\ge d}$ be the number of vertices in 
$T_n$ that have degree d and degree at least d, respectively (we omit the dependence on n for these variables throughout). The variables 
$(Z_d)_{d\ge 0}$ are referred to as the degree sequence of 
$T_n$; its asymptotic joint distribution is described by the limiting normal distribution, as 
$n\to \infty$, of certain urn models in [Reference Janson32].
The tails of the degree sequence are predominantly studied in two different ranges. The sequence 
$(Z_{d + \lfloor \log_2 n\rfloor})_{d\in \mathbb{Z}}$ represents degrees close to the maximum degree. Its limiting joint distribution is described (along suitable subsequences) by an explicit Poisson point process in 
$\mathbb{Z}\cup \{\infty\}$ in [Reference Addario-Berry and Eslava2]; the lattice shift by 
$\log_2 n$ stems from the fact that 
$\Delta_n/\log_2 n$, the renormalized maximum degree in 
$T_n$, converges almost surely (a.s.) to 1 [Reference Devroye and Lu20]. More generally, high-degree vertices are counted by 
$Z_{\ge c\ln n}$, for 
$c>0$, and their moments are described in [Reference Addario-Berry and Eslava2]. The techniques developed in [Reference Eslava24] provide bounds on the total variation distance between 
$Z_{\ge c\ln n}$ and a Poisson random variable with mean 
$n^\alpha$ with a suitable 
$\alpha=\alpha(c)$ for 
$c\in (1, \log_2 n)$.
Our main results concern 
$Z_{\ge D}$, a tail of the degree sequence of 
$T_n$ with random index. More precisely, let 
$D=D(n)$ denote the degree of the root in 
$T_n$ and let 
$Z_{\ge D}$ denote the number of vertices with degree at least D. Although the root degree D is concentrated around 
$\ln n$ (see, e.g., (2.5)), its tails do not vanish sufficiently fast. This leads us to consider the variable 
$\ln Z_{\geq D}$ instead of directly analyzing 
$Z_{\ge D}$.
The first theorem provides convergence in probability, after a normalization by 
$\ln n$. Its proof is based on the concentration of D and the first- and second-moment methods for suitable tails 
$Z_{\ge d}$; see Section 2.
Theorem 1.1. Let 
$\gamma\;:\!=\;1-\ln 2$; then the following convergence in probability holds:
\[ \dfrac{\ln Z_{\geq D} }{\ln n} \stackrel{\mathbb{P}}{\longrightarrow} \gamma. \]
We also obtain matching asymptotics for the moments of 
$\ln Z_{\geq D}/\ln n$.
Theorem 1.2. Let 
$\gamma\;:\!=\;1-\ln 2$. For any positive integer k,
\begin{equation*} {\mathbb{E}}\big[(\!\ln {Z_{\geq D}})^k\big] = (\gamma \ln {n})^k (1+o(1)). \end{equation*}
To establish Theorem 1.2, we resort to a coupling between a random recursive tree 
$T_n$ of size n and a random recursive tree 
$T_n^{(\varepsilon)}$ of size n conditioned on D to take values in 
$( (1- \varepsilon) \ln n, (1 +\varepsilon)\ln n)$, for any given 
$\varepsilon\in (0,1)$; see Section 3.
Briefly described, the coupling is the following. Let 
$n\in \mathbb{N}$. For the construction of both 
$T_n$ and 
$T_n^{(\varepsilon)}$, it suffices to define the parent of vertex i, for each 
$1< i\le n$. For each tree, we break down this choice into two steps: First, sample a random Bernoulli to decide whether i attaches to the root or not. Then the parent of i is either the root or a uniformly sampled vertex among the rest of the possible parents. The Bernoulli variables corresponding to both 
$T_n$ and 
$T_n^{(\varepsilon)}$ are coupled in such a way that the root degree has the desired distribution. Additionally, if a given vertex chooses a parent distinct from the root, then this choice is precisely the same for both the unconditioned and conditioned trees.
1.2. The random cutting process and related models
There is a wide variety of random trees for which the cutting process has been analyzed. The survey by Baur and Bertoin provides a detailed description of the advances from the introduction of cutting processes in the 1970s up to 2014 [Reference Baur and Bertoin6]. In this section we provide a panoramic overview of the references therein, recent progress on the k-cut model, and further literature on resilience of networks more broadly.
The random cutting process described in the first part of the introduction naturally extends to more complex processes on RRTs. For example, it leads to the Bolthausen–Sznitman coalescent in the case of RRTs [Reference Goldschmidt and Martin27]; the construction of both the cut-tree and the tree of component sizes [Reference Baur5, Reference Baur and Bertoin6, Reference Bertoin8, Reference Bertoin9]. The last two processes are tightly related to percolation clusters of the trees.
In this section we only provide details on the results for 
$X_n$, the number of cuts needed to isolate the root of an RRT of size n, under random edge cuts. Using the splitting property, [Reference Meir and Moon43] proved that, as 
$n\to \infty$,
\begin{equation} \frac{{\mathbb{E}}[X_n]\ln n}{n} \to 1.\end{equation}
The splitting property refers to the fact that if we remove an edge from an RRT, then the two subtrees resulting from the split are in turn, conditionally on their sizes, independent RRTs. This property has been also used in [Reference Drmota, Iksanov, Möhle and Roesler23, Reference Iksanov and Möhle30, 45].
In particular, [45] improved (1.1) to convergence in probability by extending the analysis to the cost of the random cutting procedure; that is, each cut has a cost in a function of the size of the removed tree. The random variable 
$X_n$ is recovered when the cost is a constant function.
Finally, the limiting distribution of 
$X_n$, after a suitable rescaling, was obtained in [Reference Drmota, Iksanov, Möhle and Roesler23] via singularity analysis and in [Reference Iksanov and Möhle30] using probabilistic and recursive methods. Namely,
\begin{equation*} Y_n\;:\!=\;\frac{(\!\ln n)^2}{n}X_n-\ln n-\ln \ln n\end{equation*}
converges weakly to a complete asymmetric Cauchy variable Y with characteristic function given by
$$\varphi_Y(\lambda) \;:\!=\; \exp\bigg\{\textrm{i}\lambda\ln\vert\lambda\vert-\frac{\pi\vert\lambda\vert}{2}\bigg\}.$$
Other methods of selecting edges in an RRT include using the order of the vertex labels. This directly means that the number of removals to isolate the root is precisely the number of vertices attached to it; however, more can be said about the cluster evolution if we do not discard the cut trees during the process [Reference Baur and Bertoin6]. [Reference Javanian and Vahidi-As35] modified the process with the objective of isolating the last vertex added to the network. [Reference Kuba and Panholzer36–Reference Kuba and Panholzer38] focused specifically on isolating a distinguished vertex; for example, the isolation of a leaf or isolating multiple distinguished vertices.
More recently, [Reference Cai, Devroye, Holmgren and Skerman14, Reference Cai, Devroye, Holmgren and Skerman15] introduced the k-cut model, in which edges are selected uniformly at random but these are removed only after their kth selection. After the initial results for paths and some trees, this analysis has been applied to complete binary trees [Reference Cai and Holmgren16], Galton–Watson trees [Reference Berzunza, Cai and Holmgren11], and the Brownian continuum random tree [Reference Wang46].
Broadly speaking, results on the k-cut process exploit a strategy based on counting records [Reference Janson31, Reference Janson33]. This strategy consists of noting that the number of cuts needed to destroy a tree is equivalent to the number of records that arise from a random labeling of the edges. This method has also been applied for split trees and binary trees [Reference Holmgren28, Reference Holmgren29].
Cutting processes of random trees and graphs can serve as a proxy for the resilience of a particular network to breakdowns, either from intentional attacks or fortuitous events. What is considered a breakdown and resilience may differ depending on the context. In their work on RRTs, Meir and Moon consider contamination from a certain source within an organism, and we may think of the number of cuts as the necessary steps to isolate the source of the contamination [Reference Meir and Moon43]. On the other hand, malicious attacks may refer to failures that arise from a hacker or enemy trying to disconnect some given network of servers. Thus, malicious attacks can be mathematically described by targeted cutting toward highly connected servers. These ideas on resilience were posed in [Reference Cohen and Erez17, Reference Cohen and Erez18] for scale-free graphs. Later, [Reference Bollobás and Riordan12] compared random versus malicious attacks on scale-free graphs; more precisely, the comparison is on the cluster sizes in percolation versus cluster sizes after removing a constant number of the smallest-labeled vertices.
As first described in [Reference Móri44], the Albert–Barabási random tree is part of the large class of scale-free graphs that exhibit persistence of node centrality. That is, for any fixed 
$k\in \mathbb{N}$, there is a finite time (a.s.) in the evolution of the Albert–Barabási random tree such that the identity of the k largest degree vertices does not change. Interestingly for our purposes, RRTs do not exhibit such persistence of node centrality; evidence of this fact can be found in [Reference Addario-Berry and Eslava2]. [Reference Banerjee and Bhamidi4] studied the persistence of a large class of evolving networks.
Finally, we name a few similar procedures in more general graphs. [Reference Berche, von Ferber, Holovatch and Holovatch7] studied public transport networks; [Reference Xu, Si, Duan, Lv and Xie47] studied a broad range of dynamical processes, including birth–death processes, regulatory dynamics, and epidemic processes on scale-free graphs and Erdös–Renyi networks under two different targeted attacks, with both high-degree and low-degree vertices; [Reference Alenazi and Sterbenz3] compared different graph metrics, such as node betweenness, node centrality, and node degree, to measure network resilience to random and directed attacks. In the context of Galton–Watson trees, cutting down trees has been predominantly studied from the perspective of vertex cutting; that is, vertices are selected to be removed; see, e.g., [Reference Addario-Berry, Broutin and Holmgren1, Reference Bertoin and Miermont10, Reference Dieuleveut21].
1.3. Targeted cutting for RRTs
Let 
$T_n$ be an RRT of size n and enumerate its vertices as 
$(v^{(i)})_{i=1}^{n}$ according to the decreasing order of their degrees; that is, 
$\deg(v^{(1)})\geq \cdots \geq \deg (v^{(n)})$, breaking ties uniformly at random. The targeted vertex-cutting process is performed by sequentially removing vertices 
$v^{(1)}, v^{(2)}, \ldots, v^{(n)}$ and keeping only the subtree containing the root after each removal (skip a step if the chosen vertex has previously been removed). The procedure ends when the root is picked to be removed.
Let 
$K_n$ denote the number of vertex deletions before we select the root to be removed. Similarly to the random cutting of trees, 
$K_n$ corresponds to the number of (largest) records on vertex degrees along paths from the root towards the leaves. However, there is a lack of understanding of the structure of vertices with high degree. The study of the location of high-degree vertices was initiated by the first author by establishing asymptotic results on the depth of vertices conditioned to have high degrees [Reference Eslava25]. The same approach was later extended to include the label of such vertices [Reference Lodewijks39]. Both the maximum degree and the label of a vertex attaining such a maximum have been asymptotically described for a more general class of weighted RRTs [Reference Eslava, Lodewijks and Ortgiese26, Reference Lodewijks40, Reference Lodewijks and Ortgiese41].
Also, the splitting property cannot be exploited in the targeted cutting procedure. In this case, the first vertex that is deleted, 
$v^{(1)}$, is conditioned on having the largest degree. To the best of our knowledge, the distribution of the size of the subtree rooted at 
$v^{(1)}$ remains unknown.
Now, recall that 
$Z_{\ge D}$ denotes the number of vertices in 
$T_n$ which have degree at least the degree of the root. This random variable corresponds to the quenched worst-case scenario for the deletion time of the targeted cutting. That is, once the tree has been sampled and all the degrees are known, 
$Z_{\ge D} $ is a natural upper bound for 
$K_n$: when all the vertices in the list which have degree at least D have been deleted, then the root (and so the complete tree) has been deleted.
Theorem 1.1 provides a stochastic upper bound for 
$K_n$, the deletion time of the targeted cutting process in RRTs.
Proposition 1.1. The random number of cuts 
$K_n$ in the targeted cutting of 
$T_n$ satisfies, for any 
$\varepsilon>0$, 
$K_n=O_p(n^{\gamma+\varepsilon})$, where 
$\gamma\;:\!=\;1-\ln 2$. Namely, for each 
$\delta>0$, there are 
$M=M(\varepsilon,\delta)>0$ and 
$N=N(\varepsilon, \delta) \in \mathbb{N}$ such that, for all 
$n\ge N$, 
${\mathbb{P}}(K_n> M n^{\gamma+\varepsilon})<\delta$.
Proof. Theorem 1.1 implies that the result is satisfied for 
$\varepsilon,\delta>0$. Indeed, let N be large enough that 
${\mathbb{P}}(Z_{\ge D}\ge n^{\gamma +\varepsilon})<\delta$ for 
$n\ge N$. The result follows, setting 
$M(\varepsilon,\delta)=1$, since 
$K_n\le Z_{\geq D}$ a.s.
Note that removing a uniformly random edge is equivalent to removing a uniformly chosen vertex other than the root. This difference may be neglected in the case of RRTs, so we can compare (1.1), in its probability version, with 
$K_n=O_p(n^{\gamma+\varepsilon})$. While Proposition 1.1 provides only a stochastic upper bound for 
$K_n$, it proves that the targeted cutting deletion time is significantly smaller compared to the deletion time for uniformly random removals (note that 
$1-\ln{2}\approx 0.306\,85$).
The upper bound 
$K_n\le Z_{\geq D}$ may not be tight for two reasons. First, some of the vertices in the list may not be deleted, but rather removed when some ancestor is deleted, and second, the root may not be the last vertex, among those with the same degree, to be deleted. We perform simulations that suggest 
$K_n$ and 
$Z_{\geq D}$ have the same growth order; see Section 4.
1.4. Notation
We use 
$|A|$ to denote the cardinality of a set A. For 
$n\in\mathbb{N}$ we write 
$[n]\;:\!=\;\{1,2,\dots, n\}$ and, for 
$m<n$, 
$[m,n]=\{m,m+1,\ldots, n\}$. For 
$a,b, c,x\in \mathbb{R}$ with 
$b,c>0$, we use 
$x\in(a\pm b)c$ as an abbreviation for 
$(a-b)c\leq x\leq (a+b)c$. In what follows we denote natural and base 2 logarithms by 
$\ln$ and 
$\log$, respectively. We often use the identity 
$\ln a =\ln 2\cdot \log a$ for 
$a>0$.
For 
$r\in\mathbb{R}$ and 
$a\in\mathbb{N}$ define the falling factorial 
$(r)_a\;:\!=\;r(r-1)\cdots (r-a+1)$ and 
$(r)_0=1$. For real functions f, g we write 
$f(x)=o(g(x))$ when 
$\lim_{x\to \infty} f(x)/g(x) =0$ and 
$f(x)=O(g(x))$ when 
$|f(x)/g(x)|\le C$ for some 
$C>0$. Convergence in probability will be written as 
$\stackrel{\mathbb{P}}{\longrightarrow}$. 
$H_n$ denotes the nth harmonic number 
$H_n=\sum_{i=1}^n 1/i$. A rooted tree is a tree with a distinguished vertex, which we call the root. We always consider the edges to be directed towards the root. A directed edge 
$e=uv$ is directed from u to v and, in this case, we say that v is the parent of u. Given a rooted tree T and one of its vertices v, the degree of v in T, denoted by 
$\deg_T(v)=d_T(v)$, is the number of edges directed towards v. We say that T has size n if it has n vertices, and [n] will denote the set of vertices of a tree of size n.
2. Deterministic tails of the degree sequence
Given a random recursive tree 
$T_n$, let 
$Z_{\geq d}$ denote the number of vertices with degree at least d, that is
\begin{equation} Z_{\geq d} \equiv Z_{\geq d}(n) \;:\!=\; \vert \{v\in[n]\colon d_{T_n}(v)\geq d\}\vert.\end{equation}
Recall that 
$Z_{\ge D}$ has random index 
$D=D(n)$ which corresponds to the degree of the root in 
$T_n$. Our theorems build upon results on the convergence of the variables 
$Z_{\ge d}$; note that these variables are non-increasing on d. The following two propositions are simplified versions of [Reference Addario-Berry and Eslava2, Proposition 2.1] and [Reference Eslava24, Theorem 1.8], respectively.
Proposition 2.1. (Moments of 
$Z_{\ge d}$.) For any 
$d\in \mathbb{N}$, 
${\mathbb{E}}[Z_{\ge d}]\le 2^{\log n-d}$. Moreover, there exists 
$\alpha>0$ such that, if 
$d < \frac{3}{2}\ln n$ and 
$k\in \{1,2\}$ then
\begin{align} {\mathbb{E}}[(Z_{\ge d})_k] & = 2^{(\log n-d)k}(1+o(n^{-\alpha})), \nonumber \\ {\mathbb{E}}\big[Z_{\geq d}^2\big] & = {\mathbb{E}}[Z_{\geq d}]^2(1+o(n^{-\alpha})). \end{align}
Proposition 2.2. (Total variation distance.) Let 
$0<\varepsilon<\frac{1}{3}$. Then for 
$(1+\varepsilon)\ln n< d< (1+3\varepsilon)\ln n$ there exists 
$\alpha'=\alpha'(\varepsilon)>0$ such that 
$\textrm{d}_{\textrm{TV}}(Z_{\geq d},\textrm{Poi}({\mathbb{E}}[Z_{\geq d}])) \leq O(n^{-\alpha'})$.
As we mentioned before, the error bounds in the previous propositions are not strong enough to estimate the moments of 
$Z_{\ge D}$. Instead, we focus on the variable 
$\ln Z_{\ge D}$. Furthermore, we transfer the task of moment estimation, for Theorem 1.2, to 
${\mathbb{E}}[(\!\ln X)^\ell]$ where instead of having 
$X=Z_{\ge D}$ we consider either 
$1+Z_{\ge m_-}$ or 
$1+Z_{\ge m_+}$ for suitable values 
$m_\pm=c_\pm\ln n$ with 
$c_-<1<c_+$.
The upper bound in the following proposition follows from a straightforward application of Jensen’s inequality, together with Proposition 2.1, while the lower bound uses the refined bounds given in Proposition 2.2.
Proposition 2.3. Let 
$\varepsilon\in(0,\frac{1}{3})$ and 
$\ell\in\mathbb{N}$. Let
$$ m_-\;:\!=\; \bigg\lfloor\bigg(1-\frac{\varepsilon}{2\ln 2}\bigg)\ln n\bigg\rfloor, \qquad m_+\;:\!=\; \bigg\lceil\bigg(1+\frac{\varepsilon}{2\ln 2}\bigg)\ln n +1\bigg\rceil. $$
There exist 
$\alpha'=\alpha'(\varepsilon)>0$ and 
$C_\ell=C_\ell(\varepsilon)>0$ such that
\begin{align} {\mathbb{E}}[(\!\ln\!(1+Z_{\geq m_-}))^\ell] & \leq [(1-\ln 2+\varepsilon)\ln n]^\ell + C_\ell, \end{align}
\begin{align} {\mathbb{E}}[(\!\ln\!(1+Z_{\geq m_+}))^\ell] & \geq [(1-\ln 2-\varepsilon)\ln n]^\ell(1-O(n^{-\alpha'})). \end{align}
Proof. First, let 
$f(x)=(\!\ln\!(x))^\ell$ and note that 
$f''(x)\leq 0$ for 
$x>{\textrm{e}}^{\ell-1}$. Hence, by Jensen’s inequality, for any positive integer-valued random variable X,
\[ {\mathbb{E}}[(\!\ln X)^\ell] = {\mathbb{E}}\big[(\!\ln X)^\ell\mathbf{1}_{\{X>{\textrm{e}}^{\ell -1}\}}\big] + {\mathbb{E}}\big[(\!\ln X)^\ell\mathbf{1}_{\{X\leq{\textrm{e}}^{\ell-1}\}}\big] \leq (\!\ln{\mathbb{E}}[X])^\ell + (\ell-1)^\ell. \]
Next, we use the upper bound in Proposition 2.1 for 
${\mathbb{E}}[Z_{\geq m_-}]$. Note that 
$\log n - m_-\le (1-\ln 2+{\varepsilon}/{2})\log n$. Thus, 
${\mathbb{E}}[1+Z_{\geq m_-}] \le 1+2n^{1-\ln 2+{\varepsilon}/{2}} \le n^{1-\ln 2+\varepsilon}$, where the second inequality holds for 
$n \geq n_0=n_0(\varepsilon)$ large enough. Then
\begin{equation*} {\mathbb{E}}[(\!\ln\!(1+Z_{\geq m_-}))^\ell] \leq [\ln{\mathbb{E}}[1+Z_{\geq m_-}]]^\ell + (\ell-1)^\ell \leq [(1-\ln 2+\varepsilon)\ln n]^\ell + C_\ell, \end{equation*}
where 
$C_\ell = \sup_{n\leq n_0}\{(\!\ln\!(1+2n^{1-\ln 2+{\varepsilon}/{2}}))^\ell\}+(\ell-1)^\ell$.
Next, let 
$\mu={\mathbb{E}}[Z_{\geq m_+}]$ and let (X, X ′) be random variables coupled so that 
$X \overset{\textrm{D}}{=} Z_{\geq m_+}$, 
$X' \overset{\textrm{D}}{=} \textrm{Poi}(\mu)$, and 
${\mathbb{P}}(X=X')$ is maximized; that is, 
${\mathbb{P}}(X\neq X')=\textrm{d}_{\textrm{TV}}(X,X')$. Note that
\begin{equation*} {\mathbb{E}}[(\!\ln\!(1+X))^\ell] \geq {\mathbb{E}}\big[(\!\ln\!(1+X))^\ell{\mathbf 1}_{[X> n^{\gamma-\varepsilon}]}\big] \geq (\!\ln\!(n^{\gamma-\varepsilon}))^\ell{\mathbb{P}}(X>n^{\gamma-\varepsilon}); \end{equation*}
then (2.4) boils down to lower bounding 
${\mathbb{P}}(X>n^{\gamma-\varepsilon})$. Since 
$X<n$, by the coupling assumption, we have
\begin{align*} {\mathbb{P}}(X>n^{\gamma-\varepsilon}) & \ge {\mathbb{P}}(n^{\gamma-\varepsilon}<X'<n)-{\mathbb{P}}(X\neq X') \\ & = 1-{\mathbb{P}}(X'\ge n)-{\mathbb{P}}(X'\le n^{\gamma-\varepsilon})-\textrm{d}_{\textrm{TV}}(X, X'). \end{align*}
By Proposition 2.2, 
$\textrm{d}_{\textrm{TV}}(X, X')=O(n^{-\alpha'})$ for 
$\alpha'(\varepsilon)>0$. Using the Chernoff bounds for the tails of a Poisson variable (see, e.g., [Reference Boucheron, Lugosi and Massart13, Section 2.2]) and that 
$\mu=n^{\gamma-{\varepsilon}/{2}}(1+o(1))$ we have
\begin{align*} {\mathbb{P}}(X'\ge n) & \le \bigg(\frac{{\textrm{e}} n^{\gamma-{\varepsilon}/{2}}}{n}\bigg)^n{\textrm{e}}^{-n^{\gamma-{\varepsilon}/{2}}} \le \bigg(\frac{{\textrm{e}}^{n^{\ln 2}}}{{\textrm{e}} n^{\ln 2}}\bigg)^{-n}, \\ {\mathbb{P}}(X'\le n^{\gamma-\varepsilon}) & \le \bigg(\frac{{\textrm{e}} n^{\gamma-{\varepsilon}/{2}}}{n^{\gamma-\varepsilon}}\bigg)^{n^{\gamma-\varepsilon}} {\textrm{e}}^{-n^{\gamma-{\varepsilon}/{2}}} \le \bigg(\frac{{\textrm{e}}^{n^{\varepsilon/2}}}{{\textrm{e}} n^{{\varepsilon}/{2}}}\bigg)^{-n^{\gamma-\varepsilon}}; \end{align*}
both bounds are 
$o(n^{-\alpha'})$, so the proof is completed.
2.1. Proof of Theorem 1.1
We use the first- and second-moment methods, together with Proposition 2.1, the concentration of D, and the fact that, for each n, 
$Z_{\geq m}$ is non-increasing in m.
Proof of Theorem 1.1. For completeness, we show that D is concentrated around 
$\ln n$ (in fact, it is asymptotically normal; see, e.g., [Reference Drmota22, Section 3.1.1, (6.3)] or [Reference Devroye19, Section 3]). Indeed, D is a sum of independent Bernoulli random variables 
$(B_i)_{1<i\le n}$, each with mean 
$1/(i-1)$, and so 
${\mathbb{E}}[D]=H_{n-1}> \ln n$. From the fact that 
$H_n-\ln n$ is a decreasing sequence we infer that, for any 
$0<\varepsilon<\frac32$ and n sufficiently large, 
$|D-H_{n-1}| \le ({\varepsilon}/{2}) H_{n-1}$ implies 
$|D-\ln n|\le \varepsilon \ln n$. Using the contrapositive of this statement and Bernstein’s inequality (see, e.g., [Reference Janson, Łuczak and Rucinski34, Theorem 2.8]) we obtain, for n large enough,
\begin{equation} {\mathbb{P}}(D \notin (1\pm\varepsilon)\ln n) \leq {\mathbb{P}}(\vert D-H_{n-1}\vert > ({\varepsilon}/{2})H_{n-1}) \leq 2\exp\bigg\{{-}\frac{\varepsilon^2}{12}H_{n-1}\bigg\} \leq 2n^{-\varepsilon^2/12}. \end{equation}
Recall that 
$\gamma=1-\ln 2$. It suffices to prove that, for every 
$\varepsilon>0$,
\[\lim_{n\to\infty}{\mathbb{P}}(Z_{\geq D}\notin(n^{\gamma-\varepsilon},n^{\gamma+\varepsilon})) = 0.\]
We infer from (2.5) that 
${\mathbb{P}}(Z_{\geq D}\notin(n^{\gamma-\varepsilon},n^{\gamma+\varepsilon}),D\notin(1\pm\varepsilon)\ln n)$ vanishes as n grows.
Let 
$m_- \;:\!=\; m_-(\varepsilon ) = \lfloor (1-\varepsilon)\ln n \rfloor$ and 
$m_+\;:\!=\; m_+(\varepsilon) =\lceil (1+\varepsilon)\ln n \rceil$. Using the monotonicity of 
$Z_{\ge m}$ on m, we have
\begin{equation} {\mathbb{P}}(Z_{\geq D}\notin(n^{\gamma-\varepsilon},n^{\gamma+\varepsilon}),D\in(1\pm\varepsilon)\ln n) \leq {\mathbb{P}}(Z_{\geq m_-}\geq n^{\gamma+\varepsilon})+{\mathbb{P}}(Z_{\geq m_+}\leq n^{\gamma-\varepsilon}), \end{equation}
so it remains to show that both terms on the right-hand side of (2.6) vanish. First, using that 
$\ln n=\ln 2\cdot \log n$ and so 
$\log n-(1\pm\varepsilon)\ln n=(1-\ln 2\mp\varepsilon\ln 2)\log n$, we infer from Proposition 2.1 that
\begin{equation*} \frac{1}{2}n^{\gamma-\varepsilon\ln 2}(1-o(n^{-\alpha})) \le {\mathbb{E}}[Z_{\geq m_+}] \le {\mathbb{E}}[Z_{\geq m_-}] \leq 2n^{\gamma+\varepsilon\ln 2}. \end{equation*}
Markov’s inequality then gives 
${\mathbb{P}}(Z_{\geq m_-}\geq n^{\gamma+\varepsilon}) \leq 2n^{-\varepsilon\gamma}\to 0$. Next, let 
$\theta$ be defined so that 
$n^{\gamma-\varepsilon}=\theta {\mathbb{E}}[Z_{\geq m_+}]$; in particular, 
$\theta\le 2n^{-\varepsilon\gamma}$. The Paley–Zygmund inequality gives
\begin{equation*} {\mathbb{P}}(Z_{\geq m_+} > n^{\gamma-\varepsilon}) \ge {\mathbb{P}}(Z_{\geq m_+} > \theta{\mathbb{E}}[Z_{\geq m_+}]) \geq (1-\theta)^2\frac{{\mathbb{E}}[Z_{\geq m_+}]^2}{{\mathbb{E}}\big[Z_{\geq m_+}^2\big]}, \end{equation*}
which tends to 1 as 
$n\to \infty$ by the upper bound for 
$\theta$ and (2.2). This implies that 
${\mathbb{P}}(Z_{\geq m_+}\le n^{\gamma-\varepsilon})$ vanishes, as desired.
3. Control of D through a coupling
Let 
$n\in \mathbb{N}$. Write 
$\mathcal{I}_n$ for the set of increasing trees of size n; namely, labeled rooted trees with label set [n] such that the vertex labels are increasing along any path starting from the root. It is straightforward to verify that the law of 
$T_n$ is precisely the uniform distribution on 
$\mathcal{I}_n$.
Consider the following construction of an increasing tree of size n. Let 
$(b_i)_{1<i\le n}$ and 
$(y_i)_{1<i\le n}$ be integer-valued sequences such that 
$b_2=y_2=1$, 
$b_i\in \{0,1\}$, and 
$2\le y_i\le i-1$ for 
$3\le i\le n$. Let the vertex labeled 1 be the root and, for each 
$1<i \le n$, let vertex i be connected to vertex 1 if 
$b_i=1$; otherwise, let vertex i be connected to vertex 
$y_i$.
The following coupling is exploited in the proof of Theorem 1.2. Define random vectors 
$(B_i)_{1<i\le n}$, 
$\big(B_i^{(\varepsilon)}\big)_{1<i \le n}$, and 
$(Y_i)_{1<i\le n}$ as follows. Let 
$(B_i)_{1<i \le n}$ be independent 
$\textrm{Bernoulli}({1}/({i-1}))$ random variables, let 
$\big(B_i^{(\varepsilon)}\big)_{1<i \le n}$ have the law of 
$(B_i)_{1<i \le n}$ conditioned on 
$\sum_{i=2}^{n} B_i \in (1\pm\varepsilon)\ln\!(n)$, and let 
$(Y_i)_{1<i\le n}$ be independent random variables such that 
$Y_2=1$ a.s. and 
$Y_i$ is uniform over 
$\{2, \ldots, i-1\}$ for 
$3\le i\le n$. We assume that the vector 
$(Y_i)_{1<i\le n}$ is independent from the rest, while the coupling of 
$(B_i)_{1<i\le n}$ and 
$\big(B_i^{(\varepsilon)}\big)_{1<i \le n}$ is arbitrary.
The tree obtained from 
$(B_i)_{1<i\le n}$, 
$(Y_i)_{1<i\le n}$, and the construction above has the distribution of an RRT. To see this, write 
$v_i$ for the parent of vertex i; then 
$1\le v_i<i$ for each 
$1<i\le n$. First, note that each 
$v_i$ is independent from the rest since 
$(B_i)_{1<i\le n}$ and 
$(Y_i)_{1<i\le n}$ are independent. Next, we show that 
$v_i$ is chosen uniformly at random from 
$\{1,2,\dots,i-1\}$. First, we have 
$v_2=1$ almost surely. For 
$2\le \ell< i\le n$, by the independence of 
$B_i$ and 
$Y_i$, we have
\begin{equation*} {\mathbb{P}}(v_i=1) = {\mathbb{P}}(B_i=1) = \frac{1}{i-1} = {\mathbb{P}}(B_i=0,Y_i=\ell)={\mathbb{P}}(v_i=\ell);\end{equation*}
therefore, the tree obtained has the law of an RRT and so we denote it by 
$T_n$. Analogously, write 
$T_n^{(\varepsilon)}$ for the tree obtained from 
$\big(B_i^{(\varepsilon)}\big)_{1<i \le n}$ and 
$(Y_i)_{1<i\le n}$, and let 
$D^{(\varepsilon)}$ be the degree of its root.
By the definition of D and the construction above we have 
$D=\sum_{i=2}^n B_i$. Thus, conditioning on 
$\sum_{i=2}^n B_i$ means, under this construction, conditioning 
$T_n$ on the root degree D. In particular, the distribution of 
$\big(B_i^{(\varepsilon)}\big)_{1< i\le n}$ is defined so that 
$T_n^{(\varepsilon)}$ has the distribution of an RRT of size n conditioned on 
$D^{(\varepsilon)}\in (1\pm\varepsilon)\ln\!(n)$.
The condition 
$D^{(\varepsilon)}\in(1\pm\varepsilon)\ln n$ corresponds to an event of probability close to 1 and so the degree sequences of 
$T_n$ and 
$T_n^{(\varepsilon)}$ do not differ by much. Hence, the proof strategy of Theorem 1.2 is to estimate the moments 
${\mathbb{E}}[(\!\ln Z_{\ge D})^k]$ using the monotonicity of 
$Z_{\geq d}$, by conditioning on 
$D\in (1\pm \varepsilon) \ln n$ while retaining 
$Z_{\geq d}$ instead of 
$Z_{\geq d}^{(\varepsilon)}$; see (3.9)–(3.11).
The following two propositions make this idea rigorous. For 
$d\ge 0$, let
\begin{equation*} W_d = \frac{1+Z_{\geq d}^{(\varepsilon)}}{1+Z_{\geq d}},\end{equation*}
where 
$Z_{\geq d}$ is defined as in (2.1) and, similarly, let 
$Z_{\geq d}^{(\varepsilon)}\;:\!=\;\big|\big\{v\in T_n^{(\varepsilon)} :\, d_{T_n^{(\varepsilon)}}(v)\geq d\big\}\big|$.
The key in the proof of Proposition 3.1 lies in (3.3), which yields an upper bound on the number of vertices that have differing degrees in 
$T_n$ and 
$T_n^{(\varepsilon)}$ under the coupling. In turn, this allows us to infer bounds on the ratio 
$W_d$ that hold with high probability and are uniform in d.
Proposition 3.1. Let 
$\varepsilon,\delta\in(0,1)$ and 
$0\le d \leq (1+\varepsilon)\ln n$. There are 
$C>0$, 
$\beta=\beta(\varepsilon)>0$, and 
$n_0=n_0(\delta)$ such that, for 
$n\geq n_0$, under the coupling described above, 
${\mathbb{P}}(W_d\in(1\pm\delta)) \geq 1-Cn^{-\beta}$.
Proof. Let 
$m_+=\lceil(1+\varepsilon)\ln n\rceil$, so that 
$Z_{\geq d} \geq Z_{\geq m_+}$. By Chebyshev’s inequality and (2.2), for 
$c\in (0,1)$,
\begin{equation} {\mathbb{P}}(Z_{\geq m_+} \le c{\mathbb{E}}[Z_{\ge m_+}]) \leq {\mathbb{P}}(\vert Z_{\geq m_+}-{\mathbb{E}}[Z_{\geq m_+}]\vert \geq (1-c){\mathbb{E}}[Z_{\ge m_+}]) = o(n^{-\alpha}). \end{equation}
Rewrite
$$W_d=1+\frac{Z_{\ge d}^{(\varepsilon)}-Z_{\ge d}}{1+Z_{\ge d}}$$
to see that 
$W_d\in (1\pm \delta)$ is equivalent to 
$\big|Z_{\ge d}^{(\varepsilon)}-Z_{\ge d}\big| \in [0,\delta(1+Z_{\ge d}))$. Hence, it suffices to show that there is 
$n_0(\delta)\in \mathbb{N}$ such that, for 
$n\ge n_0$,
\begin{equation} \{Z_{\ge m_+}\ge c{\mathbb{E}}[Z_{\ge m_+}],D\in(1\pm\varepsilon)\ln n\} \subset \big\{\big|Z_{\ge d}^{(\varepsilon)}-Z_{\ge d}\big|\leq\delta(1+ Z_{\ge d})\big\}, \end{equation}
which, by a contrapositive argument, together with (2.5) and (3.1), yields, for 
$\beta=\min{\{\alpha,\varepsilon^2/12\}}>0$,
\begin{equation*} {\mathbb{P}}\big(\big|Z_{\ge d}^{(\varepsilon)}-Z_{\ge d}\big|>\delta(1+ Z_{\ge d})\big) \le {\mathbb{P}}(D\notin(1\pm\varepsilon)\ln n) + {\mathbb{P}}(Z_{\ge m_+}\le c{\mathbb{E}}[Z_{\ge m_+}]) = O(n^{-\beta}). \end{equation*}
We extend the notation introduced for the coupling. Let 
${\mathcal{S}}\;:\!=\;\{i\in [2,n]\colon v_i=v_i^{(\varepsilon)}\}$ be the set of vertices that have the same parent in 
$T_n$ and 
$T_n^{(\varepsilon)}$. For 
$i\in [n]$, denote the set of children of i in 
$T_n$ and 
$T_n^{(\varepsilon)}$, respectively, by
\begin{equation*} \mathcal{C}(i) \;:\!=\; \{j\in [2,n]\colon v_j=i\}, \qquad \mathcal{C}^{(\varepsilon)}(i)\;:\!=\;\{j\in [2,n]\colon v_j^{(\varepsilon)}=i\}. \end{equation*}
By the coupling construction, 
${\mathcal{S}} \cup (\mathcal{C}(1)\bigtriangleup \mathcal{C}^{(\varepsilon)}(1))$ is a partition of [2,n]; that is, whenever the parent of a vertex 
$i\in [2,n]$ differs in 
$T_n$ and 
$T_n^{(\varepsilon)}$ we infer that 
$B_i\neq B_i^{(\varepsilon)}$ and so either 
$i\in \mathcal{C}(1)\setminus \mathcal{C}^{(\varepsilon)}(1)$ or 
$i\in \mathcal{C}(1)^{(\varepsilon)}\setminus \mathcal{C}(1)$. The consequences of this observation are two-fold: First, for any 
$i\in [2,n]$, a necessary condition for 
$d_{T_n}(i)\neq d_{T_{n}^{(\varepsilon)}}(i)$ is that 
$\mathcal{C}(i)\neq \mathcal{C}^{(\varepsilon)}(i)$; second, the function 
$j\mapsto Y_j$ that maps 
$\mathcal{C}(1) \bigtriangleup \mathcal{C}^{(\varepsilon)}(1)$ to 
$\{i\in[2,n]\colon\mathcal{C}(i)\neq\mathcal{C}^{(\varepsilon)}(i)\}$ is surjective. Indeed, if 
$i\neq 1$ and 
$\mathcal{C}(i)\neq \mathcal{C}^{(\varepsilon)}(i)$ then there exists 
$j\in \mathcal{C}(1) \bigtriangleup \mathcal{C}^{(\varepsilon)}(1)$ such that 
$Y_j=i$. Together they imply the following chain of inequalities:
\begin{equation} \big|\big\{i\in[2,n]\colon d_{T_n}(i)\neq d_{T_{n}^{(\varepsilon)}}(i)\big\}\big| \le |\{i\in[2,n]\colon\mathcal{C}(i)\neq\mathcal{C}^{(\varepsilon)}(i)\}| \le \vert\mathcal{C}(1)\bigtriangleup\mathcal{C}(1)^{(\varepsilon)}\vert; \end{equation}
the first inequality holds by containment of the corresponding sets, while the second one follows from the surjective function described above. On the other hand, 
$\vert Z_{\geq d}-Z_{\geq d}^{(\varepsilon)}\vert$ equals
\begin{align*} \Bigg\vert\sum_{i=1}^n \mathbf{1}_{\{d_{T_n}(i) \geq d\}}(i) - \sum_{i=1}^n \mathbf{1}_{\{d_{T_n^{(\varepsilon)}}(i) \geq d\}}(i)\Bigg\vert & \leq \sum_{i=1}^n\big\vert\mathbf{1}_{\{d_{T_n}(i) \geq d\}}(i) - \mathbf{1}_{\{d_{T_n^{(\varepsilon)}}(i) \geq d\}}(i)\big\vert \\ & \leq 1 + \big|\big\{i\in\{2,\ldots,n\}\colon d_{T_n}(i)\neq d_{T_n^{(\varepsilon)}}(i)\big\}\big|. \end{align*}
Therefore,
\begin{equation} \big\vert Z_{\geq d}-Z_{\geq d}^{(\varepsilon)}\big\vert \leq 1 + \vert\mathcal{C}(1) \bigtriangleup \mathcal{C}^{(\varepsilon)}(1)\vert \le 1 + 2\max\{|\mathcal{C}(1)|, |\mathcal{C}^{(\varepsilon)}(1)|\}. \end{equation}
We are now ready to prove (3.2). Fix, e.g., 
$c=\frac12$ and let 
$n_0=n_0(\delta)$ be large enough that 
$({1+4\ln n})/{\delta}<c{\mathbb{E}}[Z_{\geq m_+}]$; this is possible since 
${\mathbb{E}}[Z_{\geq m_+}]$ grows polynomially in n, by Proposition 2.1. In particular, recalling that 
$Z_{\ge d}\ge Z_{\ge m_+}$ for 
$n\ge n_0$ and any 
$\varepsilon\in(0,1)$, we have
\begin{equation} \{Z_{\ge m_+} \geq c{\mathbb{E}}[Z_{\ge m_+}]\} \subset \bigg\{Z_{\geq d} \geq \frac{1+2(1+\varepsilon)\ln n}{\delta}\bigg\}. \end{equation}
Moreover, by the construction of 
$T_n^{(\varepsilon)}$, 
$|\mathcal{C}(1)^{(\varepsilon)}|=D^{(\varepsilon)}\le (1+\varepsilon)\ln n$, so that (3.4) implies
\begin{equation*} \bigg\{Z_{\geq d} \geq \frac{1+2(1+\varepsilon)\ln n}{\delta}, D\in (1\pm \varepsilon)\ln n\bigg\} \subset \big\{\big|Z_{\ge d}^{(\varepsilon)}-Z_{\ge d}\big|\leq\delta(1+ Z_{\ge d})\big\}; \end{equation*}
note that this holds for all 
$n\in \mathbb{N}$. Together with (3.5), this implies (3.2) for 
$n\ge n_0$, as desired.
Proposition 3.2. Let 
$\varepsilon\in (0,1)$, 
$\ell \in \mathbb{N}$. For 
$0\le d \leq (1+\varepsilon)\ln n$, there is a 
$\beta=\beta(\varepsilon)>0$ such that, under the coupling described above, 
$\vert{\mathbb{E}}[(\!\ln W_d)^\ell]\vert \leq O((\!\ln n)^\ell n^{-\beta})+1$.
Proof. We first simplify to 
$\vert{\mathbb{E}}[(\!\ln W_d)^\ell]\vert \le {\mathbb{E}}[|(\!\ln W_d)^\ell|] \le {\mathbb{E}}[|\ln W_d|^\ell]$. Note that 
${1}/{n}\leq W_d\leq n$ for every 
$0 \le d\le (1\pm\varepsilon)\ln n$. Indeed, it is straightforward that 
$W_0\equiv 1$ and, for 
$d\ge 1$, the bounds follow since any tree has at least one vertex of degree zero and so 
$\max\big\{Z_{\ge d}, Z_{\ge d}^{(\varepsilon)}\big\}<n$. Then, for any 
$\delta \in(0,1)$,
\begin{align*} {\mathbb{E}}[|\ln W_d|^\ell{\mathbf 1}_{[W_d<1-\delta]}] & \le (\!\ln n)^\ell{\mathbb{P}}(W_d<1-\delta), \\ {\mathbb{E}}[|\ln W_d|^\ell{\mathbf 1}_{[W_d>1+\delta]}] & \le (\!\ln n)^\ell{\mathbb{P}}(W_d>1+\delta). \end{align*}
Proposition 3.1 implies that these two terms are 
$O((\!\ln n)^\ell n^{-\beta})$, where the implicit constant depends on the choice of 
$\delta$. With foresight, fix 
$\delta$ to satisfy 
$({\delta}/({1-\delta}))^\ell + \delta^\ell = 1$. Using that 
$1-({1}/{x}) \leq \ln x\le x-1$ for all 
$x\geq 0$,
\begin{align*} {\mathbb{E}}[|\ln W_d|^\ell{\mathbf 1}_{[W_d\in (1\pm \delta)]}] & \le {\mathbb{E}}\bigg[\bigg|1-\frac{1}{W_d}\bigg|^\ell{\mathbf 1}_{[W_d\in (1- \delta, 1)]}\bigg] + {\mathbb{E}}[|W_d-1|^\ell{\mathbf 1}_{[W_d\in [1, 1+ \delta)]}] \\ & \le \bigg(\frac{\delta}{1-\delta}\bigg)^\ell + \delta^\ell = 1, \end{align*}
and so the result follows.
3.1. Proof of Theorem 1.2
Proof of Theorem 1.2. Fix 
$k\in\mathbb{N}$ and recall that 
$\gamma\;:\!=\;1-\ln\!(2)$. Suppose that, for any 
$\varepsilon\in\big(0,\frac{1}{3}\big)$, there exist 
$c=c(\varepsilon)>0$ and 
$C=C(k,\varepsilon)>0$ such that
\begin{equation} ((\gamma-\varepsilon)\ln n)^k(1+O(n^{-c})) - C \leq {\mathbb{E}}[(\!\ln Z_{\geq D})^k] \leq ((\gamma+\varepsilon) \ln n)^k + C. \end{equation}
It is straightforward to verify that (3.6) establishes Theorem 1.2. So, it remains to prove (3.6).
Let 
$\varepsilon'=\varepsilon/(2\ln\!(2))$ and write 
$m_-= \lfloor (1-\varepsilon')\ln n \rfloor$, 
$m_+=\lceil (1+\varepsilon')\ln n +1 \rceil$. We focus on the term 
${\mathbb{E}}[(\!\ln Z_{\geq D})^k\mathbf{1}_{\{D\in(1\pm\varepsilon')\ln n\}}]$, as (2.5) and 
$1\le Z_{\ge D}\le n$ imply
\begin{equation} 0 \le {\mathbb{E}}[(\!\ln Z_{\geq D})^k\mathbf{1}_{\{D\notin(1\pm\varepsilon')\ln n\}}] \le (\!\ln n)^k{\mathbb{P}}(D\notin(1\pm\varepsilon')\ln n) = (\!\ln n)^k O(n^{-\varepsilon'/12}). \end{equation}
Using the monotonicity of 
$Z_{\ge d}$, we have
\begin{equation*} {\mathbb{E}}[(\!\ln Z_{\geq D})^k\mathbf{1}_{\{D\in(1\pm\varepsilon')\ln n\}}] \le {\mathbb{E}}[(\!\ln Z_{\geq m_-})^k\mathbf{1}_{\{D\in(1\pm\varepsilon')\ln n\}}] \le {\mathbb{E}}[(\!\ln Z_{\geq m_-})^k], \end{equation*}
which, by (2.3), yields
\begin{equation} {\mathbb{E}}[(\!\ln Z_{\geq D})^k\mathbf{1}_{\{D\in(1\pm\varepsilon')\ln n\}}] \le ((\gamma+\varepsilon)\ln n)^k +C_k. \end{equation}
For the lower bound, recall the variable 
$Z^{(\varepsilon')}_{\geq d}$ defined in the previous section with 
$d=m_+$. Observe that, if 
$D\in (1\pm \varepsilon')\ln n$, then 
$Z_{\ge D}\ge 1 + Z_{m_+}$, and we thus obtain
\begin{align} {\mathbb{E}}[(\!\ln{Z_{\geq D}})^k\mathbf{1}_{\{D\in(1\pm\varepsilon')\ln n\}}] & \ge {\mathbb{E}}[(\!\ln\!(1+Z_{\geq m_+}))^k\mathbf{1}_{\{D\in(1\pm\varepsilon')\ln n\}}] \nonumber \\ & \ge {\mathbb{E}}\big[\big(\!\ln\big(1+Z^{(\varepsilon')}_{\geq m_+}\big)\big)^k\big] {\mathbb{P}}(D\in(1\pm\varepsilon')\ln n). \end{align}
The definition of 
$W_d$ gives
\begin{equation} \ln\big(1+Z_{\geq m_+}^{(\varepsilon')}\big) = \ln\!\bigg(\big(1+Z_{\geq m_+}^{(\varepsilon')}\big)\frac{1+Z_{\geq m_+}}{1+Z_{\geq m_+}}\bigg) = \ln\!(1+Z_{\geq m_+}) + \ln{W_{m_+}}; \end{equation}
similarly, for 
$k\ge 2$, the binomial expansion implies
\begin{equation} \big(\!\ln\big(1+Z_{\geq m_+}^{(\varepsilon')}\big)\big)^k = (\!\ln\!(1+Z_{\geq m_+}))^k + \sum_{\ell=1}^{k}\binom{k}{\ell}\ln\!(1+Z_{\geq m_+})^{k-\ell}(\!\ln W_{m_+})^\ell. \end{equation}
We use (2.4) for a lower bound on the expectation of the main term in these last two decompositions. For the error terms involving 
$W_{m_+}$ we use Proposition 3.2. If 
$k=1$, we directly get
\begin{align*} {\mathbb{E}}\big[\ln\big(1+Z_{m_+}^{(\varepsilon')}\big)\big] & = {\mathbb{E}}[\ln\!(1+Z_{\geq m_+})] + {\mathbb{E}}[\ln{W_{m_+}}] \\ & \ge (\gamma-\varepsilon)\ln n(1+O(n^{-\alpha'})) + O((\!\ln n)n^{-\beta}) - 1. \end{align*}
If 
$k\ge 2$, we control each of the terms in the sum of (3.11). For 
$1\le \ell\le k$, the Cauchy–Schwarz inequality gives
\begin{equation*} \vert{\mathbb{E}}[(\!\ln\!(1+Z_{\geq m_+}))^{k-\ell}(\!\ln W_{m_+})^\ell]\vert \leq {\mathbb{E}}[(\!\ln\!(1+Z_{\geq m_+}))^{2(k-\ell)}]^{1/2}{\mathbb{E}}[(\!\ln W_{m_+})^{2\ell}]^{1/2}. \end{equation*}
The deterministic bound 
$Z_{\ge m_+}<n$ implies 
${\mathbb{E}}[(\!\ln\!(1+Z_{\ge m_-}))^{2(k-\ell)}]^{1/2} \le (\!\ln n)^{k-\ell}$. On the other hand, Proposition 3.2 yields
\begin{equation*} {\mathbb{E}}[(\!\ln W_{m_+})^{2\ell}]^{1/2} \leq (O((\!\ln n)^{2\ell}n^{-\beta})+1)^{1/2} \le O((\!\ln n)^{\ell}n^{-\beta})+1. \end{equation*}
Thus, after taking expectations in (3.11), we get
\begin{equation} {\mathbb{E}}\big[\big(\!\ln\big(1+Z^{(\varepsilon')}_{\geq m_+}\big)\big)^k\big] \ge ((\gamma-\varepsilon)\ln n)^k(1-o(n^{-c}))-C, \end{equation}
where 
$c=\min\{\alpha',\beta\}$ and 
$C=\max\{C_k,2^k\}$. Then, (3.7), (3.8), and (3.12) together with (2.5) imply (3.6), completing the proof.
4. Simulations
The approach of counting the number of records, although difficult in directly studying 
$K_n$, provides us with a way to test our results via simulations in Python. We implement an algorithm that identifies the number of (largest) vertex-degree records; in the case of ties, we keep track of a set of uniform random variables that determines the order of deletion of vertices with the same degree. See Appendix A.
We obtain 10 000 samples of RRTs of size 
$100\,000$ and use the data to graph Figures 1 and 2. Figure 1 shows the empirical distribution of both 
$K_n$ and 
$Z_{\ge D}$. The distributions appear to follow a power law. However, due to the nature of the variables under study, this computational probe is far from providing a better insight. We compare the empirical distributions of 
$K_n$ and 
$Z_{\geq D}$ using a Q–Q plot, shown in Figure 2. From this plot, it seems that 
$Z_{\geq D}$ and 
$K_n$ share similar behavior.
Figure 1. Empirical distributions of 
$K_{100\,000}$ and 
$Z_{\geq D}(100\,000)$ using a sample of size 10 000.
Figure 2. Q–Q plot for 
$Z_{\geq D}(100\,000)$ and 
$K_{100\,000}$ using a sample size of 10 000.
To further explore the growth behavior of 
${\mathbb{E}}[K_n]$ and 
${\mathbb{E}}[Z_{\geq D}]$, we generate 10 000 samples of RRTs of 50 different tree sizes, equally spaced on a logarithmic scale. Figure 3 shows the mean for each size, together with 
$n^\gamma$ as a comparison. A shortcoming we found was that since 
$\ln n$ varies slowly, it was difficult to obtain a deeper insight into this resemblance.
Figure 3. Estimates for 
${\mathbb{E}}[Z_D]$ and 
${\mathbb{E}}[K_n]$ in logarithmic scale, given a sample size of 10 000.
Summing up, the simulations provide limited yet useful information. The Q–Q plot in Figure 2 contributes to our understanding of the process since it may suggest that 
$K_n$ and 
$Z_{\geq D}$ have the same growth order.
5. Conclusion and open problems
In this paper we introduced the notion of targeted cutting of a random recursive tree. This procedure serves as a proxy for the resilience of a particular network to malicious attacks from an enemy. To a certain extent, this problem has been tackled for scale-free random networks, where the malicious strategy boils down to removing a given proportion of the smallest-labeled vertices, regardless of the structure of the graph. The reason for this is mainly because preferential attachment models have the property of persistence, which refers to the fact that high-degree vertices are fixed early in the process. In contrast, RRTs lack persistence and the picture for high-degree vertices in RRTs is more nuanced and far less complete.
Our results provide the first quantitative estimate for the deletion time 
$K_n$ of the targeted cutting process for random recursive trees. To do so, we shifted the focus to 
$Z_{\ge D}$, the number of vertices with degree at least as large as the degree of the root; this random variable corresponds to the quenched worst-case scenario for 
$K_n$.
In our main theorems, we found that 
$\ln Z_{\ge D}$ grows as 
$\ln n$ asymptotically and obtains its limiting behavior in probability. Moreover, we obtained the growth order of the kth moment of 
$\ln Z_{\ge D}$ for 
$k\ge 1$.
Proposition 1.1, confirms the intuition that the targeted procedure requires substantially fewer cuts than the random edge deletion procedure. This result was obtained by observing that, once the tree has been sampled and all the degrees are known, 
$Z_{\ge D} $ is an upper bound for 
$K_n$. Unfortunately, the sensitivity that 
$Z_{\ge D}$ may provide for the targeted cutting procedure is limited since it fails to consider the structure of 
$T_n$, in particular high-degree vertices.
It remains open to understand the structure of the tree induced by, say, the first 
$k=k(n)$ vertices with highest degree. In turn, this could shed light on a theoretical analysis of vertex-degree records. Similarly, we may study the sizes of the subtrees of maximal degree vertices, in order to exploit the splitting property for cutting processes.
On the other hand, analyzing 
$Z_{\ge D}$ in more detail is not a straightforward task. It would be interesting to sharpen the results on 
$Z_{\ge c\ln n}$ for a wider range of 
$c\ge 0$ for RRTs and, more generally, weighted RRTs.
Appendix A. The targeted cutting time algorithm
We use a depth-first search algorithm to simulate 
$K_n$, as this variable corresponds to the number of (largest) records of vertex degrees in paths from the root to the leaves, which is denoted by C below.
Given 
$n\in \mathbb{N}$, generate an RRT 
$T_n$ where, initially, each vertex v stores its degree 
$d_{T_n}(v)$ and its parent 
$P_v$, and set 
$R_v=\deg_{T_n}(v)$, 
$L_v=v$. Let C be a counting variable initialized to 1 (because the root itself is a record). Using a depth-first search exploration, each vertex v compares its degree, 
$d_{T_n}(v)$, with the current record of its parent, 
$R_{P_v}$. Additionally, 
$L_v$ keeps track of the largest degree vertex encountered in its path to the root.
We encounter three cases:
1. If
$d_{T_n}(v)< R_{P_v}$, set $R_v=R_{P_v}$ and $L_v=L_{P_v}$. In the cutting process, v is removed because one of its ancestors is deleted.-
2. If
$d_{T_n}(v)> R_{P_v}$, update $C=C+1$. That is, v is removed before any of its ancestors and so v counts as a record. -
3. If
$d_{T_n}(v)= R_{P_v}$, then let U(v) and $U(L_{P_v})$ be independent $\textrm{Uniform}(0,1)$ random variables (note that $U(L_{P_v})$ may already have been generated). If $U(v)<U(L_{P_v})$, proceed as in step 1, otherwise proceed as in step 2.
Return the variable C.
Funding information
Sergio I. López was supported by DGAPA-PAPIIT-UNAM grant IN-102822, and Marco L. Ortiz was supported by CONACYT grant 955991.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.
Open access
