Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-22T05:25:28.109Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasi-stationary distributions in semi-Markov processes

Published online by Cambridge University Press:  14 July 2016

C. K. Cheong
C. K. Cheong*
Affiliation:
University of Malaya
Get access Rights & Permissions [Opens in a new window]

Abstract

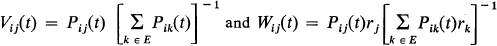Our main concern in this paper is the convergence, as t → ∞, of the quantities i, j ∈ E; where Pij(t) is the transition probability of a semi-Markov process whose state space E is irreducible but not closed (i.e., escape from E is possible), and rj is the probability of eventual escape from E conditional on the initial state being i. The theorems proved here generalize some results of Seneta and Vere-Jones ([8] and [11]) for Markov processes.

Type
Research Papers
Information
Journal of Applied Probability , Volume 7 , Issue 2 , August 1970 , pp. 388 - 399
Copyright
Copyright © Applied Probability Trust 1970 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Cheong, C. K. (1968) Ergodic and ratio limit theorems for a-recurrent semi-Markov processes. Z. Wahrscheinlichkeitsth. 9, 270–286.Google Scholar
[2] Cheong, C. K. A note on the key renewal theorem. To appear.Google Scholar
[3] Cox, D. R. (1962) Renewal Theory. Methuen, London.Google Scholar
[4] Darroch, J. N. and Seneta, E. (1965) On quasi-stationary distributions in absorbing discrete finite Markov chains. J. Appl. Prob. 2, 88–100.CrossRefGoogle Scholar
[5] Kingman, J. F. C. (1963) The exponential decay of Markov transition probabilities. Proc. Lond. Math. Soc. 13, 337–358.Google Scholar
[6] Kingman, J. F. C. (1963) Ergodic properties of continuous-time Markov processes and their discrete skeletons. Proc. Lond. Math. Soc. 13, 593–604.CrossRefGoogle Scholar
[7] Pyke, R. and Schaufele, R. (1964) Limit theorems for Markov renewal processes. Ann. Math. Statist. 35, 1746–1764.CrossRefGoogle Scholar
[8] Seneta, E. and Vere-Jones, D. (1966) On quasi-stationary distributions in discrete-time Markov chains with a denumerable infinity of states. J. Appl. Prob. 3, 403–434.Google Scholar
[9] Vere-Jones, D. (1962) Geometric ergodicity in denumerable Markov chains. Quart. J. Math. 13, 7–28.CrossRefGoogle Scholar
[10] Vere-Jones, D. (1967) Ergodic properties of non-negative matrices-I. Pacific J. Math. 22, 361–386.Google Scholar
[11] Vere-Jones, D. (1969) Some limit theorems for evanescent processes. Aust. J. Statist. 11, 67–78.Google Scholar
[12] Widder, D. V. (1946) The Laplace Transform. University Press, Princeton.Google Scholar