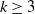1. Introduction and results
The study of random polygons induced by a Poisson process of random lines in the plane is among the most classical topics in stochastic geometry. The distribution of a stationary Poisson line process
![]() $X=X(\gamma,G)$
in the plane is completely determined by its intensity
$X=X(\gamma,G)$
in the plane is completely determined by its intensity
![]() $\gamma>0$
and its directional distribution G. For us, the latter is a probability measure on the interval
$\gamma>0$
and its directional distribution G. For us, the latter is a probability measure on the interval
![]() $[0,\pi)$
satisfying
$[0,\pi)$
satisfying
![]() $G(\theta)<1$
for each
$G(\theta)<1$
for each
![]() $\theta\in[0,\pi)$
. We refer to the monographs [Reference Matheron9] and [Reference Stoyan, Kendall and Mecke15] for further background material and detailed descriptions and explanations. The typical cell
$\theta\in[0,\pi)$
. We refer to the monographs [Reference Matheron9] and [Reference Stoyan, Kendall and Mecke15] for further background material and detailed descriptions and explanations. The typical cell
![]() $Z=Z(\gamma,G)$
of a stationary Poisson line tessellation with intensity
$Z=Z(\gamma,G)$
of a stationary Poisson line tessellation with intensity
![]() $\gamma$
and directional distribution G can intuitively be thought of as a random polygon selected ‘uniformly at random’ among the collection of all polygons (in a very large observation window) induced by X, regardless of size and shape. It is a classical descriptor of the statistical properties of the random polygons generated by this Poisson line process. Formally, its distribution can be defined using Palm calculus as explained in detail in [Reference Stoyan, Kendall and Mecke15]; see also (2.4) below. The geometry of the typical cell of a Poisson line tessellation and its analogue in higher dimensions has been investigated intensively over the past few decades, and numerous articles are dedicated to the study of its size or its combinatorial structure. As examples we mention the articles [Reference Calka3], [Reference George5], [Reference Miles11], [Reference Miles12], and [Reference Tanner16], which deal with first- and second-order moments as well as integral expressions in the planar case, and the works [Reference Bonnet, Calka and Reitzner2], [Reference Favis and Weiß4], [Reference Hug and Schneider6], [Reference Mecke10], [Reference Schneider13], and [Reference Schneider14], which mainly discuss first-order properties in higher-dimensional situations.
$\gamma$
and directional distribution G can intuitively be thought of as a random polygon selected ‘uniformly at random’ among the collection of all polygons (in a very large observation window) induced by X, regardless of size and shape. It is a classical descriptor of the statistical properties of the random polygons generated by this Poisson line process. Formally, its distribution can be defined using Palm calculus as explained in detail in [Reference Stoyan, Kendall and Mecke15]; see also (2.4) below. The geometry of the typical cell of a Poisson line tessellation and its analogue in higher dimensions has been investigated intensively over the past few decades, and numerous articles are dedicated to the study of its size or its combinatorial structure. As examples we mention the articles [Reference Calka3], [Reference George5], [Reference Miles11], [Reference Miles12], and [Reference Tanner16], which deal with first- and second-order moments as well as integral expressions in the planar case, and the works [Reference Bonnet, Calka and Reitzner2], [Reference Favis and Weiß4], [Reference Hug and Schneider6], [Reference Mecke10], [Reference Schneider13], and [Reference Schneider14], which mainly discuss first-order properties in higher-dimensional situations.
However, despite the many results just mentioned, even in the planar case, for most of the geometric and combinatorial quantities the precise distribution is unknown and even good approximation results are rarely available. In particular, this is the case for the number of vertices of the typical cell Z, which is the principal object we study in this paper. More precisely, we are interested in the exact probability that Z takes the simplest possible shape: a triangle. Since the intensity
![]() $\gamma$
only acts as a scaling parameter, this probability cannot depend on
$\gamma$
only acts as a scaling parameter, this probability cannot depend on
![]() $\gamma$
and we can take
$\gamma$
and we can take
![]() $\gamma=1$
for simplicity and write Z(G) instead of Z(1, G). Further, we define the triangle probability
$\gamma=1$
for simplicity and write Z(G) instead of Z(1, G). Further, we define the triangle probability
which can equivalently be described as the proportion of triangles among the polygons of the Poisson line tessellation:
where
![]() $B_R$
stands for a disk of radius
$B_R$
stands for a disk of radius
![]() $R>0$
centred at the origin and the sum runs over all tessellation cells c contained in
$R>0$
centred at the origin and the sum runs over all tessellation cells c contained in
![]() $B_R$
. If the directional distribution
$B_R$
. If the directional distribution
![]() $G=G_{\rm unif}$
is the uniform distribution on
$G=G_{\rm unif}$
is the uniform distribution on
![]() $[0,\pi)$
and the Poisson line tessellation is isotropic, it has been known since [Reference Miles11] (see Theorem 6 therein) that
$[0,\pi)$
and the Poisson line tessellation is isotropic, it has been known since [Reference Miles11] (see Theorem 6 therein) that
compare also with [Reference Miles12] and with the computations indicated in Section 3. A realization of an isotropic Poisson line process is shown in Figure 1(c). In Section 5 we will provide an alternative proof for (1.1) using new results from the present paper. We further remark that in the isotropic case too the probability
is known from [Reference Tanner16]. However, for
![]() $k\geq 5$
the probabilities
$k\geq 5$
the probabilities
![]() $\mathbb{P}[Z(G_{\rm unif})\text{ has exactly} \textit{k} \text{vertices}]$
can be expressed only as rather involved multiple integrals, which can be evaluated numerically; see [Reference Calka3]. On the other hand, it is well known that the expected number of vertices of the typical cell is 4, independently of the choice of the directional distribution G; see [Reference Stoyan, Kendall and Mecke15, Section 10.5.1].
$\mathbb{P}[Z(G_{\rm unif})\text{ has exactly} \textit{k} \text{vertices}]$
can be expressed only as rather involved multiple integrals, which can be evaluated numerically; see [Reference Calka3]. On the other hand, it is well known that the expected number of vertices of the typical cell is 4, independently of the choice of the directional distribution G; see [Reference Stoyan, Kendall and Mecke15, Section 10.5.1].

Figure 1. Simulation of a Poisson line tessellation with directional distribution
![]() $G_3$
(a),
$G_3$
(a),
![]() $G_4$
(b), and
$G_4$
(b), and
![]() $G_{\rm unif}$
(c).
$G_{\rm unif}$
(c).
At the other extreme, if G is concentrated on only two different values, all cells are almost surely parallelograms. So in this case we have
![]() $p_3(G)=0$
. Thus the next non-trivial case arises if the directional distribution G is concentrated on three different values. For simplicity and concreteness we start with the case where G is given by
$p_3(G)=0$
. Thus the next non-trivial case arises if the directional distribution G is concentrated on three different values. For simplicity and concreteness we start with the case where G is given by
where we write
![]() $\delta_{(\cdot)}$
for the Dirac measure and where
$\delta_{(\cdot)}$
for the Dirac measure and where
![]() $p,q\in(0,1)$
are weights satisfying
$p,q\in(0,1)$
are weights satisfying
![]() $0<p+q<1$
. In other words,
$0<p+q<1$
. In other words,
![]() $G_3(p,q)$
is concentrated on the angles 0,
$G_3(p,q)$
is concentrated on the angles 0,
![]() $\pi/3$
, and
$\pi/3$
, and
![]() $2\pi/3$
with weights p, q, and
$2\pi/3$
with weights p, q, and
![]() $1-p-q$
, respectively. A simulation of a Poisson line tessellation with directional distribution
$1-p-q$
, respectively. A simulation of a Poisson line tessellation with directional distribution
![]() $G_3(1/3,1/3)$
is shown in Figure 1(a). We remark that a stationary Poisson line process with directional distribution
$G_3(1/3,1/3)$
is shown in Figure 1(a). We remark that a stationary Poisson line process with directional distribution
![]() $G_3(1/3,1/3)$
is of course not invariant under all rotations in the plane. However, it is invariant under rotations whose angle is an integer multiple of
$G_3(1/3,1/3)$
is of course not invariant under all rotations in the plane. However, it is invariant under rotations whose angle is an integer multiple of
![]() $\pi/3$
. The corresponding Poisson line tessellation can thus be called
$\pi/3$
. The corresponding Poisson line tessellation can thus be called
![]() $G_3(1/3,1/3)$
-pseudo-isotropic.
$G_3(1/3,1/3)$
-pseudo-isotropic.
Our first result is a formula for
![]() $p_3(G_3(p,q))$
in terms of the weights p and q. Also, we determine those weights for which
$p_3(G_3(p,q))$
in terms of the weights p and q. Also, we determine those weights for which
![]() $p_3(G_3(p,q))$
attains its maximal value; see Figure 2.
$p_3(G_3(p,q))$
attains its maximal value; see Figure 2.
Theorem 1.1.
For all
![]() $0<p,q<1$
with
$0<p,q<1$
with
![]() $0<p+q<1$
, we have
$0<p+q<1$
, we have
The maximal value for
![]() $p_3(G_3(p,q))$
is attained precisely if
$p_3(G_3(p,q))$
is attained precisely if
![]() $p=q=1/3$
and is given by
$p=q=1/3$
and is given by
It is a special feature of the case of three directions that the formula for the triangle probability carries over to general orientation angles.

Figure 2. A plot of
![]() $p_3(G_3(p,q))$
.
$p_3(G_3(p,q))$
.
Corollary 1.1.
Fix
![]() $0\leq \varphi_1<\varphi_2<\varphi_3<\pi$
, weights
$0\leq \varphi_1<\varphi_2<\varphi_3<\pi$
, weights
![]() $p,q\in(0,1)$
with
$p,q\in(0,1)$
with
![]() $0<p+q<1$
, and consider the directional distribution
$0<p+q<1$
, and consider the directional distribution
![]() $G\,:\!=\, p\delta_{\varphi_1}+q\delta_{\varphi_2}+(1-p-q)\delta_{\varphi_3}$
. Then
$G\,:\!=\, p\delta_{\varphi_1}+q\delta_{\varphi_2}+(1-p-q)\delta_{\varphi_3}$
. Then
![]() $p_3(G)=p_3(G_3(p,q))$
with
$p_3(G)=p_3(G_3(p,q))$
with
![]() $p_3(G_3(p,q))$
as in Theorem 1.1.
$p_3(G_3(p,q))$
as in Theorem 1.1.
In analogy with the case of three directions just studied, one can consider a Poisson line tessellation with directional distribution
![]() $G_4(p,q,r)\,:\!=\, p\delta_0+q\delta_{{\pi}/{ 4}}+r\delta_{{\pi}/{ 2}}+(1-p-q-r)\delta_{{(3\pi)}/{ 4}}$
with weights
$G_4(p,q,r)\,:\!=\, p\delta_0+q\delta_{{\pi}/{ 4}}+r\delta_{{\pi}/{ 2}}+(1-p-q-r)\delta_{{(3\pi)}/{ 4}}$
with weights
![]() $0<p,q,r<1$
satisfying
$0<p,q,r<1$
satisfying
![]() $0<p+q+r<1$
, as shown in Figure 1(b). The corresponding triangle probability is in this case given by
$0<p+q+r<1$
, as shown in Figure 1(b). The corresponding triangle probability is in this case given by
 \begin{align*} &p_3(G_4(p,q,r))\\ &\quad =\dfrac{2 p}{\sqrt{2}p+2q+\sqrt{2}r-\sqrt{2}p^2-2q^2-\sqrt{2}r^2-2pq+(2-2\sqrt{2})pr-2qr}\\ &\quad \quad \times\biggl(\dfrac{3 q r}{{2+p({-}2+\sqrt{2})-q+r({-}2+\sqrt{2})}} +\dfrac{3\sqrt{2} q(1-p-q-r)}{2+({-}2+\sqrt{2}) p+r({-}2+2\sqrt{2})}\\ &\quad \quad \quad +\dfrac{2r\sqrt{2}(1-p-q-r)}{\sqrt{2}+p(2-\sqrt{2})+\sqrt{2}q+r(2-\sqrt{2})}\biggr),\end{align*}
\begin{align*} &p_3(G_4(p,q,r))\\ &\quad =\dfrac{2 p}{\sqrt{2}p+2q+\sqrt{2}r-\sqrt{2}p^2-2q^2-\sqrt{2}r^2-2pq+(2-2\sqrt{2})pr-2qr}\\ &\quad \quad \times\biggl(\dfrac{3 q r}{{2+p({-}2+\sqrt{2})-q+r({-}2+\sqrt{2})}} +\dfrac{3\sqrt{2} q(1-p-q-r)}{2+({-}2+\sqrt{2}) p+r({-}2+2\sqrt{2})}\\ &\quad \quad \quad +\dfrac{2r\sqrt{2}(1-p-q-r)}{\sqrt{2}+p(2-\sqrt{2})+\sqrt{2}q+r(2-\sqrt{2})}\biggr),\end{align*}
as demonstrated in [Reference Krecklenberg8]. Since the triangle probabilities for five or more directions with arbitrary weights become increasingly more involved, from now on we concentrate on the special case where all weights are equal. Namely, for integers
![]() $k\geq 3$
we take as directional distribution the probability measure
$k\geq 3$
we take as directional distribution the probability measure
 \[G_k \,:\!=\, \dfrac{1}{ k}\sum_{\ell=0}^{k-1}\delta_{{(\ell\pi)}/{ k}},\]
\[G_k \,:\!=\, \dfrac{1}{ k}\sum_{\ell=0}^{k-1}\delta_{{(\ell\pi)}/{ k}},\]
which for
![]() $k=3$
and
$k=3$
and
![]() $k=4$
reduces to
$k=4$
reduces to
![]() $G_3(1/3,1/3)$
and
$G_3(1/3,1/3)$
and
![]() $G_4(1/4,1/4,1/4)$
, respectively. In other words,
$G_4(1/4,1/4,1/4)$
, respectively. In other words,
![]() $G_k$
puts weight
$G_k$
puts weight
![]() $1/k$
onto k equally spread directions. The Poisson line tessellation induced by such a directional distribution is
$1/k$
onto k equally spread directions. The Poisson line tessellation induced by such a directional distribution is
![]() $G_k$
-pseudo-isotropic in the sense that it is invariant under rotations in the plane whose angle is an integer multiple of
$G_k$
-pseudo-isotropic in the sense that it is invariant under rotations in the plane whose angle is an integer multiple of
![]() $\pi/k$
. In our second result we determine the triangle probabilities
$\pi/k$
. In our second result we determine the triangle probabilities
![]() $p_3(G_k)$
.
$p_3(G_k)$
.
Theorem 1.2.
For
![]() $k\geq 3$
we have that
$k\geq 3$
we have that
 \begin{align*}p_3(G_k) &= \dfrac{4}{ k}\tan^2\dfrac{\pi}{ 2k}\sum_{i=1}^{k-2}\Biggl[(k-i)\sum_{j=1}^{k-i-1}\dfrac{\sin\frac{i\pi}{ k}\,\sin\frac{j\pi}{ k}\,\sin\frac{(i+j)\pi}{ k}}{\sin\frac{i\pi}{ k}+\sin\frac{j\pi}{ k}+\sin\frac{(i+j)\pi}{ k}}\Biggr].\end{align*}
\begin{align*}p_3(G_k) &= \dfrac{4}{ k}\tan^2\dfrac{\pi}{ 2k}\sum_{i=1}^{k-2}\Biggl[(k-i)\sum_{j=1}^{k-i-1}\dfrac{\sin\frac{i\pi}{ k}\,\sin\frac{j\pi}{ k}\,\sin\frac{(i+j)\pi}{ k}}{\sin\frac{i\pi}{ k}+\sin\frac{j\pi}{ k}+\sin\frac{(i+j)\pi}{ k}}\Biggr].\end{align*}
The exact and approximate values for
![]() $p_3(G_k)$
for
$p_3(G_k)$
for
![]() $k\in\{3,4,5,6\}$
are summarized in the table in Figure 3(a), some further values are visualized in Figure 3(b). The latter also shows that, as
$k\in\{3,4,5,6\}$
are summarized in the table in Figure 3(a), some further values are visualized in Figure 3(b). The latter also shows that, as
![]() $k\to\infty$
, the value
$k\to\infty$
, the value
![]() $p_3(G_k)$
tends to
$p_3(G_k)$
tends to
![]() $2-{\pi^2/ 6}=p_3(G_{\rm unif})$
, the triangle probability appearing in the isotropic case. This observation is confirmed in the following corollary.
$2-{\pi^2/ 6}=p_3(G_{\rm unif})$
, the triangle probability appearing in the isotropic case. This observation is confirmed in the following corollary.

Figure 3. (a) Concrete values of
![]() $p_3(G_k)$
for
$p_3(G_k)$
for
![]() $k=3,4,5,6$
. (b) Visualization of values of
$k=3,4,5,6$
. (b) Visualization of values of
![]() $p_3(G_k)$
for
$p_3(G_k)$
for
![]() $k=3,4,\dots,15$
and the limiting value
$k=3,4,\dots,15$
and the limiting value
![]() $p_3(G_{\rm unif})$
(dashed line).
$p_3(G_{\rm unif})$
(dashed line).
Corollary 1.2.
For
![]() $k\ge3$
, let
$k\ge3$
, let
![]() $p_3(G_k)$
be as in Theorem 1.2. Then
$p_3(G_k)$
be as in Theorem 1.2. Then
![]() $\lim_{k\to\infty}p_3(G_k)= p_3(G_{\rm unif})$
.
$\lim_{k\to\infty}p_3(G_k)= p_3(G_{\rm unif})$
.
The proof of both Theorem 1.1 and Theorem 1.2 is based on the sampling procedure for the typical cell of stationary Poisson line tessellation developed in [Reference George5]. It generalizes one of the stochastic constructions described in [Reference Miles12] to general directional distributions. To keep the paper reasonably self-contained we recall the relevant elements of this construction in the next section. Then in Section 3 we show how the probability
![]() $p_3(G_{\rm unif})$
can be determined using this sampling procedure. Using the same approach, the proofs of Theorem 1.1, Theorem 1.2, and Corollary 1.2 are the subject of Section 4. The final section of this paper provides an alternative proof of Miles’s result (1.1) regarding the proportion of triangles in an isotropic Poisson line tessellation.
$p_3(G_{\rm unif})$
can be determined using this sampling procedure. Using the same approach, the proofs of Theorem 1.1, Theorem 1.2, and Corollary 1.2 are the subject of Section 4. The final section of this paper provides an alternative proof of Miles’s result (1.1) regarding the proportion of triangles in an isotropic Poisson line tessellation.
2. Sampling random triangles
In this paper a line is parametrized by a pair
![]() $(\theta,d)$
, where
$(\theta,d)$
, where
![]() $d\in\mathbb{R}$
is the signed distance of the line to the origin and
$d\in\mathbb{R}$
is the signed distance of the line to the origin and
![]() $\theta\in[0,\pi)$
is the north-east angle this line makes with the horizontal; see Figure 4. We refer to
$\theta\in[0,\pi)$
is the north-east angle this line makes with the horizontal; see Figure 4. We refer to
![]() $\theta$
as the orientation angle of the line.
$\theta$
as the orientation angle of the line.

Figure 4. A line L parametrized by
![]() $(d,\theta)$
.
$(d,\theta)$
.
Following [Reference George5], it will turn out to be convenient to extend the range of the possible orientation angles to the larger interval
![]() $[{-}\pi,\pi)$
, where negative angles should be thought of modulo
$[{-}\pi,\pi)$
, where negative angles should be thought of modulo
![]() $\pi$
. For example, we identify the orientation angles
$\pi$
. For example, we identify the orientation angles
![]() $-\pi/3$
and
$-\pi/3$
and
![]() $2\pi/3$
.
$2\pi/3$
.
Throughout the remainder of this work, we denote random variables by a capital letter and their realizations by small ones; for example,
![]() $\Phi$
denotes a random angle and
$\Phi$
denotes a random angle and
![]() $\phi$
a given realization.
$\phi$
a given realization.
2.1. General facts about Poisson line processes
We consider a stationary Poisson line process
![]() $X=X(\gamma,G)$
with intensity
$X=X(\gamma,G)$
with intensity
![]() $\gamma>0$
and directional distribution G. We assume G to be non-degenerate, meaning that
$\gamma>0$
and directional distribution G. We assume G to be non-degenerate, meaning that
![]() $G(\theta)<1$
for each
$G(\theta)<1$
for each
![]() $\theta\in[0,\pi)$
. The following facts are taken from [Reference George5], but see also [Reference Stoyan, Kendall and Mecke15].
$\theta\in[0,\pi)$
. The following facts are taken from [Reference George5], but see also [Reference Stoyan, Kendall and Mecke15].
Intersection with a fixed line. Let L be a fixed line with orientation angle
![]() $\theta\in[0,\pi)$
. Its intersection with X is a stationary Poisson point process on L with intensity
$\theta\in[0,\pi)$
. Its intersection with X is a stationary Poisson point process on L with intensity
![]() $\gamma\lambda(\theta)$
, where
$\gamma\lambda(\theta)$
, where
see Figure 5(a). Furthermore, the random orientation angles of the lines associated with these points of intersection are independent and identically distributed with common conditional density
with respect to G.

Figure 5. (a) Intersection of a Poisson line process X (thin lines) with a fixed line
![]() $L=(\theta,d)$
(thick). (b) Lines of X (thin lines) intersecting triangle sides
$L=(\theta,d)$
(thick). (b) Lines of X (thin lines) intersecting triangle sides
![]() $T_1$
and
$T_1$
and
![]() $T_2$
but not
$T_2$
but not
![]() $T_3$
.
$T_3$
.
Intersection of two random lines. Let L and L
′ be two different lines from X, and let
![]() $(\Theta,\Theta^{\prime})$
be the two orientation angles at the intersection point
$(\Theta,\Theta^{\prime})$
be the two orientation angles at the intersection point
![]() $L\cap L^{\prime}$
. Then the pair
$L\cap L^{\prime}$
. Then the pair
![]() $(\Theta,\Theta^{\prime})$
has joint density
$(\Theta,\Theta^{\prime})$
has joint density
with respect to the product measure
![]() $G\otimes G$
on
$G\otimes G$
on
![]() $[0,\pi)\times[0,\pi)$
, where
$[0,\pi)\times[0,\pi)$
, where
Intersection with a triangle. Consider an arbitrary triangle T in the plane with sides
![]() $T_1$
,
$T_1$
,
![]() $T_2$
, and
$T_2$
, and
![]() $T_3$
having lengths
$T_3$
having lengths
![]() $t_1$
,
$t_1$
,
![]() $t_2$
,
$t_2$
,
![]() $t_3$
and whose supporting lines have orientation angles
$t_3$
and whose supporting lines have orientation angles
![]() $\theta_1$
,
$\theta_1$
,
![]() $\theta_2$
,
$\theta_2$
,
![]() $\theta_3$
, respectively. Then the number of lines of X intersecting T but do not intersect
$\theta_3$
, respectively. Then the number of lines of X intersecting T but do not intersect
![]() $T_3$
has a Poisson distribution with mean
$T_3$
has a Poisson distribution with mean
see Figure 5(b).
2.2. Stochastic construction of a typical triangle
A stochastic construction of the typical cell of a stationary Poisson line tessellation induced by a Poisson line process X with intensity
![]() $\gamma>0$
and a general directional distribution G was introduced in [Reference George5], adopting previously developed methods of [Reference Miles12] for the isotropic case. We rephrase it here in the special case of a triangle, that is, we describe the distribution of the typical cell given that it is a triangle; for brevity we refer to it as the typical triangle. Formally, the distribution
$\gamma>0$
and a general directional distribution G was introduced in [Reference George5], adopting previously developed methods of [Reference Miles12] for the isotropic case. We rephrase it here in the special case of a triangle, that is, we describe the distribution of the typical cell given that it is a triangle; for brevity we refer to it as the typical triangle. Formally, the distribution
![]() $P_Z$
of the typical cell Z of the Poisson line tessellation induced by X is given as follows. Namely, if for a polygon
$P_Z$
of the typical cell Z of the Poisson line tessellation induced by X is given as follows. Namely, if for a polygon
![]() $c\subset\mathbb{R}^2$
, m(c) is the lexicographically smallest vertex, the distribution
$c\subset\mathbb{R}^2$
, m(c) is the lexicographically smallest vertex, the distribution
![]() $P_Z$
of the random polygon Z is given by
$P_Z$
of the random polygon Z is given by
 \begin{equation}P_Z({\,\cdot\,}) \,:\!=\, \dfrac{1}{ \mathbb{E}\sum_{c\,:\, m(c)\in[0,1]^2}1}\,\mathbb{E}\sum_{c\,:\, m(c)\in[0,1]^2}{\bf 1}\{c-m(c)\in\,\cdot\,\},\end{equation}
\begin{equation}P_Z({\,\cdot\,}) \,:\!=\, \dfrac{1}{ \mathbb{E}\sum_{c\,:\, m(c)\in[0,1]^2}1}\,\mathbb{E}\sum_{c\,:\, m(c)\in[0,1]^2}{\bf 1}\{c-m(c)\in\,\cdot\,\},\end{equation}
where each sum runs over all cells c of the Poisson line tessellation with
![]() $m(c)\in[0,1]^2$
(or any other Borel set with unit area). The distribution of the typical triangle is then the conditional distribution
$m(c)\in[0,1]^2$
(or any other Borel set with unit area). The distribution of the typical triangle is then the conditional distribution
![]() $P_Z({\cdot}|Z\text{ is a triangle})$
.
$P_Z({\cdot}|Z\text{ is a triangle})$
.
Starting with the lexicographically smallest vertex of the typical triangle, we label the vertices consecutively in clockwise direction by
![]() $v_1,v_2,v_3$
. For
$v_1,v_2,v_3$
. For
![]() $i\in\{1,2,3\}$
, let
$i\in\{1,2,3\}$
, let
![]() $z_i$
be the length of the segment
$z_i$
be the length of the segment
![]() $\overline{v_iv_{i+1}}$
, where we formally put
$\overline{v_iv_{i+1}}$
, where we formally put
![]() $v_4\,:\!=\, v_1$
. Moreover, we denote the angle between
$v_4\,:\!=\, v_1$
. Moreover, we denote the angle between
![]() $\overline{v_iv_{i+1}}$
and the eastern horizontal at
$\overline{v_iv_{i+1}}$
and the eastern horizontal at
![]() $v_i$
by
$v_i$
by
![]() $\phi_i$
; see Figure 6(a). Hence
$\phi_i$
; see Figure 6(a). Hence
![]() $\phi_0$
denotes the initial angle. The typical triangle is completely determined by the 4-tuple
$\phi_0$
denotes the initial angle. The typical triangle is completely determined by the 4-tuple
![]() $(\Phi_0,\Phi_1,Z_1,\Phi_2)$
; all other angles and edge lengths (especially
$(\Phi_0,\Phi_1,Z_1,\Phi_2)$
; all other angles and edge lengths (especially
![]() $\Phi_3$
,
$\Phi_3$
,
![]() $Z_2$
, and
$Z_2$
, and
![]() $Z_3$
) can be computed from these data.
$Z_3$
) can be computed from these data.

Figure 6. (a) Construction of the random triangle
![]() $\Delta$
. (b) The random triangle
$\Delta$
. (b) The random triangle
![]() $\Delta$
(thick lines) and the random line process X
′′ (thin lines). The intersection (2.5) is the shaded polygon.
$\Delta$
(thick lines) and the random line process X
′′ (thin lines). The intersection (2.5) is the shaded polygon.
We shall now describe the (conditional) distribution of the random variables
![]() $\Phi_0$
,
$\Phi_0$
,
![]() $\Phi_1$
,
$\Phi_1$
,
![]() $Z_1$
, and
$Z_1$
, and
![]() $\Phi_2$
, which are clearly dependent.
$\Phi_2$
, which are clearly dependent.
-
• The joint density with respect to
 $G\otimes G$
of
$G\otimes G$
of
 $(\Phi_0,\Phi_1)$
is given by (2.2).
$(\Phi_0,\Phi_1)$
is given by (2.2). -
• Given
 $\Phi_1=\phi_1$
, the intersection of X with the line having orientation angle
$\Phi_1=\phi_1$
, the intersection of X with the line having orientation angle
 $\Phi_1$
is a stationary Poisson point process with intensity
$\Phi_1$
is a stationary Poisson point process with intensity
 $\lambda(\phi_1)$
according to (2.1). The distance from
$\lambda(\phi_1)$
according to (2.1). The distance from
 $v_1$
to the first point of this process above the horizontal line is exponentially distributed with mean
$v_1$
to the first point of this process above the horizontal line is exponentially distributed with mean
 $\lambda(\phi_1)$
. As a result, the conditional Lebesgue density of
$\lambda(\phi_1)$
. As a result, the conditional Lebesgue density of
 $Z_1$
given
$Z_1$
given
 $\Phi_1=\phi_1$
equals
$\Phi_1=\phi_1$
equals \[z_1\mapsto \lambda(\phi_1) \,\mathrm{e}^{-\lambda(\phi_1)z_1},\quad z_1>0.\]
\[z_1\mapsto \lambda(\phi_1) \,\mathrm{e}^{-\lambda(\phi_1)z_1},\quad z_1>0.\]
-
• Given
 $\Phi_1=\phi_1$
and
$\Phi_1=\phi_1$
and
 $Z_1=z_1$
, the random variable
$Z_1=z_1$
, the random variable
 $\Phi_2$
has densitywith respect to G. Here
$\Phi_2$
has densitywith respect to G. Here \[\phi_2\mapsto \dfrac{\sin\!(\phi_1-\phi_2)}{\int_{a(z_1)}^{\phi_1}\sin\!(\phi_1-\theta)\,G(\mathrm{d} \theta)},\quad a(z_1)\leq\phi_2<\phi_1,\]
\[\phi_2\mapsto \dfrac{\sin\!(\phi_1-\phi_2)}{\int_{a(z_1)}^{\phi_1}\sin\!(\phi_1-\theta)\,G(\mathrm{d} \theta)},\quad a(z_1)\leq\phi_2<\phi_1,\]
 $a(z_1)$
is given bywhere
$a(z_1)$
is given bywhere \[a(z_1) \,:\!=\, \arctan\biggl(\dfrac{y_1}{ x_1}\biggr) - \pi,\]
\[a(z_1) \,:\!=\, \arctan\biggl(\dfrac{y_1}{ x_1}\biggr) - \pi,\]
 $(x_1,y_1)$
are the coordinates of the first vertex
$(x_1,y_1)$
are the coordinates of the first vertex
 $v_1$
.
$v_1$
.
The construction just described leads to a random triangle
![]() $\Delta$
in the plane, which is determined by the four random variables
$\Delta$
in the plane, which is determined by the four random variables
![]() $\Phi_0$
,
$\Phi_0$
,
![]() $\Phi_1$
,
$\Phi_1$
,
![]() $\Phi_2$
, and
$\Phi_2$
, and
![]() $Z_1$
. It has the conditional distribution of the typical cell
$Z_1$
. It has the conditional distribution of the typical cell
![]() $Z=Z(\gamma,G)$
, given that Z is a triangle. To obtain from
$Z=Z(\gamma,G)$
, given that Z is a triangle. To obtain from
![]() $\Delta$
the (unconditional) typical cell
$\Delta$
the (unconditional) typical cell
![]() $Z=Z(\gamma,G)$
, let X
′ be an independent stationary Poisson line process with intensity
$Z=Z(\gamma,G)$
, let X
′ be an independent stationary Poisson line process with intensity
![]() $\gamma$
and directional distribution G. From X
′ we remove all lines hitting the first edge of
$\gamma$
and directional distribution G. From X
′ we remove all lines hitting the first edge of
![]() $\Delta$
with length
$\Delta$
with length
![]() $Z_1$
and call X
′′ the resulting collection of random lines; see Figure 6(b). Then the typical cell Z has the same distribution as
$Z_1$
and call X
′′ the resulting collection of random lines; see Figure 6(b). Then the typical cell Z has the same distribution as
where for each line L,
![]() $L^+$
denotes the closed half-space bounded by L and containing the origin; see [Reference George5].
$L^+$
denotes the closed half-space bounded by L and containing the origin; see [Reference George5].
3. Triangle probability in the isotropic case
In this section we consider the isotropic case and indicate how to compute
![]() $p_3\,:\!=\, p_3(G_{\rm unif})$
using the stochastic construction outlined in the previous section. So, let
$p_3\,:\!=\, p_3(G_{\rm unif})$
using the stochastic construction outlined in the previous section. So, let
![]() $G\,:\!=\, G_{\rm unif}$
be the uniform distribution on
$G\,:\!=\, G_{\rm unif}$
be the uniform distribution on
![]() $[0,\pi)$
with constant density
$[0,\pi)$
with constant density
![]() $\theta\mapsto\theta/\pi$
. We also recall our choice
$\theta\mapsto\theta/\pi$
. We also recall our choice
![]() $\gamma=1$
. It follows from (2.1) and (2.3) that
$\gamma=1$
. It follows from (2.1) and (2.3) that
Due to the rotation invariance of the Poisson line tessellation in the isotropic case, the distribution of the initial angle
![]() $\Phi_0$
is irrelevant and we can just choose
$\Phi_0$
is irrelevant and we can just choose
![]() $\Phi_0\equiv0$
in the construction of the typical triangle for simplicity. Then the following hold.
$\Phi_0\equiv0$
in the construction of the typical triangle for simplicity. Then the following hold.
-
• The random variable
 $\Phi_1$
has density
$\Phi_1$
has density
 $\phi_1\mapsto(\pi-\phi_1)\sin\!(\phi_1)/\pi$
, for
$\phi_1\mapsto(\pi-\phi_1)\sin\!(\phi_1)/\pi$
, for
 $0\leq\phi_1<\pi$
, which is the marginal density of the pair
$0\leq\phi_1<\pi$
, which is the marginal density of the pair
 $(\Phi_0,\Phi_1)$
with respect to the second coordinate.
$(\Phi_0,\Phi_1)$
with respect to the second coordinate. -
• The random variable
 $Z_1$
is independent of
$Z_1$
is independent of
 $\Phi_1$
and has density
$\Phi_1$
and has density
 $z_1\mapsto 2\mathrm{e}^{-{2 z_1}/{\pi}}/\pi$
, for
$z_1\mapsto 2\mathrm{e}^{-{2 z_1}/{\pi}}/\pi$
, for
 $z_1>0$
.
$z_1>0$
. -
• The random variable
 $\Phi_2$
only depends on
$\Phi_2$
only depends on
 $\Phi_1$
and has conditional density
$\Phi_1$
and has conditional density
 $\phi_2\mapsto\sin\!(\phi_1-\phi_2)/2$
, given
$\phi_2\mapsto\sin\!(\phi_1-\phi_2)/2$
, given
 $\Phi_1=\phi_1$
. Here
$\Phi_1=\phi_1$
. Here
 $\phi_1-\pi\leq\phi_2 < 0$
, since
$\phi_1-\pi\leq\phi_2 < 0$
, since
 $x_1=z_1\cos\phi_1$
,
$x_1=z_1\cos\phi_1$
,
 $y_1=z_1\sin\phi_1$
, which in turn implies
$y_1=z_1\sin\phi_1$
, which in turn implies
 $a(z_1)=\phi_1-\pi$
, independently of
$a(z_1)=\phi_1-\pi$
, independently of
 $z_1$
.
$z_1$
.
Given these distributions, the probability
![]() $p_3$
that the typical cell is a triangle can now be written as follows:
$p_3$
that the typical cell is a triangle can now be written as follows:
 \begin{align*}p_3 &= \int_0^\pi\int_0^\infty\int_0^{\phi_1-\pi} \,\mathrm{e}^{-{(\lambda(\phi_2)z_2+\lambda(\phi_3)z_3-\lambda(\phi_1)z_1)}/{2}}\\ &\quad \times \dfrac{\pi-\phi_1}{\pi}\sin\phi_1\times \dfrac{2}{\pi}\,\mathrm{e}^{-{2z_1}/{\pi}}\times \dfrac{1}{ 2}\sin\!(\phi_1-\phi_2)\,\mathrm{d} \phi_2\,\mathrm{d} z_1\,\mathrm{d} \phi_1.\end{align*}
\begin{align*}p_3 &= \int_0^\pi\int_0^\infty\int_0^{\phi_1-\pi} \,\mathrm{e}^{-{(\lambda(\phi_2)z_2+\lambda(\phi_3)z_3-\lambda(\phi_1)z_1)}/{2}}\\ &\quad \times \dfrac{\pi-\phi_1}{\pi}\sin\phi_1\times \dfrac{2}{\pi}\,\mathrm{e}^{-{2z_1}/{\pi}}\times \dfrac{1}{ 2}\sin\!(\phi_1-\phi_2)\,\mathrm{d} \phi_2\,\mathrm{d} z_1\,\mathrm{d} \phi_1.\end{align*}
In fact, in order to ensure that the typical cell is a triangle, we need to ensure that after the stochastic construction of the typical triangle, given
![]() $\Phi_1=\phi_1$
,
$\Phi_1=\phi_1$
,
![]() $Z_1=z_1$
, and
$Z_1=z_1$
, and
![]() $\Phi_2=\phi_2$
, the two edges with length
$\Phi_2=\phi_2$
, the two edges with length
![]() $z_2$
and
$z_2$
and
![]() $z_3$
are not intersected by lines of the random line process X
′′; recall (2.5). Thus, by the intersection-with-a-triangle property, the above event has probability
$z_3$
are not intersected by lines of the random line process X
′′; recall (2.5). Thus, by the intersection-with-a-triangle property, the above event has probability
![]() $\exp({-}(\lambda(\phi_2)z_2+\lambda(\phi_3)z_3-\lambda(\phi_1)z_1)/2)$
, which is the probability that a Poisson random variable with mean
$\exp({-}(\lambda(\phi_2)z_2+\lambda(\phi_3)z_3-\lambda(\phi_1)z_1)/2)$
, which is the probability that a Poisson random variable with mean
![]() $(\lambda(\phi_2)z_2+\lambda(\phi_3)z_3-\lambda(\phi_1)z_1)/2$
takes the value zero. The other terms in the above integral representation are just the densities of the random variables
$(\lambda(\phi_2)z_2+\lambda(\phi_3)z_3-\lambda(\phi_1)z_1)/2$
takes the value zero. The other terms in the above integral representation are just the densities of the random variables
![]() $\Phi_1$
,
$\Phi_1$
,
![]() $Z_1$
, and
$Z_1$
, and
![]() $\Phi_2$
.
$\Phi_2$
.
It is not difficult to verify that
which yields
Inserting this together with the values of
![]() $\lambda(\phi_1)=\lambda(\phi_2)=\lambda(\phi_3)={2/\pi}$
, we arrive at
$\lambda(\phi_1)=\lambda(\phi_2)=\lambda(\phi_3)={2/\pi}$
, we arrive at
where we have already carried out the integration with respect to
![]() $z_1$
. Rewriting the integrand by means of trigonometric identities eventually leads to (1.1); all details of the computation are contained in [Reference Krecklenberg8].
$z_1$
. Rewriting the integrand by means of trigonometric identities eventually leads to (1.1); all details of the computation are contained in [Reference Krecklenberg8].
4. Proofs
4.1. Triangle probability in the
 $\boldsymbol{G}_3(\boldsymbol{p},\boldsymbol{q})$
case: Proof of Theorem 1.1
$\boldsymbol{G}_3(\boldsymbol{p},\boldsymbol{q})$
case: Proof of Theorem 1.1
In this section we compute the triangle probability
![]() $p_3\,:\!=\, p_3(G_3(p,q))$
if the underlying directional distribution is given by (1.2), again using the stochastic construction of the typical cell. We recall that we choose
$p_3\,:\!=\, p_3(G_3(p,q))$
if the underlying directional distribution is given by (1.2), again using the stochastic construction of the typical cell. We recall that we choose
![]() $\gamma=1$
as our intensity.
$\gamma=1$
as our intensity.
Before we actually compute
![]() $p_3$
, we deal with the possible constructions for triangles with only three edge directions corresponding to the orientation angles 0,
$p_3$
, we deal with the possible constructions for triangles with only three edge directions corresponding to the orientation angles 0,
![]() $\pi/ 3$
, and
$\pi/ 3$
, and
![]() $2\pi/ 3$
. In fact we only have two ways to construct a triangle with these orientation angles, as demonstrated in Figure 7. Further, writing G for
$2\pi/ 3$
. In fact we only have two ways to construct a triangle with these orientation angles, as demonstrated in Figure 7. Further, writing G for
![]() $G_3(p,q)$
for brevity, we can now compute
$G_3(p,q)$
for brevity, we can now compute
 \begin{align*}\lambda(0) &= \int_0^\pi|\sin\theta|\,G(\mathrm{d} \theta) = q\sin\dfrac{\pi}{ 3} + (1-p-q)\sin\dfrac{2\pi}{ 3} = \dfrac{\sqrt{3}}{ 2}(1-p),\\ \lambda\biggl(\dfrac{\pi}{ 3}\biggr) &= \int_0^\pi\biggl|\sin\biggl(\theta-\dfrac{\pi}{ 3}\biggr)\biggr|\,G(\mathrm{d} \theta) \\&=p\biggl|\sin\biggl({-}\dfrac{\pi}{ 3}\biggr)\biggr|+(1-p-q)\biggl|\sin\biggl(\dfrac{2\pi}{ 3}-\dfrac{\pi}{ 3}\biggr)\biggr|=\dfrac{\sqrt{3}}{ 2}(1-q),\\\lambda\biggl(\dfrac{2\pi}{ 3}\biggr) &= \int_0^\pi\biggl|\sin\biggl(\theta-\dfrac{2\pi}{ 3}\biggr)\biggr|\,G(\mathrm{d} \theta) \\ &=p\biggl|\sin\biggl({-}\dfrac{2\pi}{ 3}\biggr)\biggr|+q\biggl|\sin\biggl(\dfrac{\pi}{ 3}-\dfrac{2\pi}{ 3}\biggr)\biggr|=\dfrac{\sqrt{3}}{ 2}(p+q),\end{align*}
\begin{align*}\lambda(0) &= \int_0^\pi|\sin\theta|\,G(\mathrm{d} \theta) = q\sin\dfrac{\pi}{ 3} + (1-p-q)\sin\dfrac{2\pi}{ 3} = \dfrac{\sqrt{3}}{ 2}(1-p),\\ \lambda\biggl(\dfrac{\pi}{ 3}\biggr) &= \int_0^\pi\biggl|\sin\biggl(\theta-\dfrac{\pi}{ 3}\biggr)\biggr|\,G(\mathrm{d} \theta) \\&=p\biggl|\sin\biggl({-}\dfrac{\pi}{ 3}\biggr)\biggr|+(1-p-q)\biggl|\sin\biggl(\dfrac{2\pi}{ 3}-\dfrac{\pi}{ 3}\biggr)\biggr|=\dfrac{\sqrt{3}}{ 2}(1-q),\\\lambda\biggl(\dfrac{2\pi}{ 3}\biggr) &= \int_0^\pi\biggl|\sin\biggl(\theta-\dfrac{2\pi}{ 3}\biggr)\biggr|\,G(\mathrm{d} \theta) \\ &=p\biggl|\sin\biggl({-}\dfrac{2\pi}{ 3}\biggr)\biggr|+q\biggl|\sin\biggl(\dfrac{\pi}{ 3}-\dfrac{2\pi}{ 3}\biggr)\biggr|=\dfrac{\sqrt{3}}{ 2}(p+q),\end{align*}

Figure 7. The two possible triangles in a Poisson line tessellation with directional distribution
![]() $G_3(p,q)$
: (a) with angles
$G_3(p,q)$
: (a) with angles
![]() $\phi_0=0$
,
$\phi_0=0$
,
![]() $\phi_1=\frac{1}{3}\pi$
, and
$\phi_1=\frac{1}{3}\pi$
, and
![]() $\phi_2=-\frac{1}{3}\pi$
, (b) with angles
$\phi_2=-\frac{1}{3}\pi$
, (b) with angles
![]() $\phi_0=\frac{1}{3}\pi$
,
$\phi_0=\frac{1}{3}\pi$
,
![]() $\phi_1=\frac{2}{3}\pi$
, and
$\phi_1=\frac{2}{3}\pi$
, and
![]() $\phi_2=0$
.
$\phi_2=0$
.
according to (2.1), which implies that
 \begin{align*} \lambda &= \int_0^\pi\lambda(\theta)\,G(\mathrm{d} \theta)\\ &=p\lambda(0)+q\lambda\biggl(\dfrac{\pi}{ 3}\biggr)+(1-p-q)\lambda\biggl(\dfrac{2\pi}{ 3}\biggr) \\ &=\sqrt{3}(p+q-p^2-q^2-pq).\end{align*}
\begin{align*} \lambda &= \int_0^\pi\lambda(\theta)\,G(\mathrm{d} \theta)\\ &=p\lambda(0)+q\lambda\biggl(\dfrac{\pi}{ 3}\biggr)+(1-p-q)\lambda\biggl(\dfrac{2\pi}{ 3}\biggr) \\ &=\sqrt{3}(p+q-p^2-q^2-pq).\end{align*}
Moreover, from (2.2) it follows that the pair
![]() $(\Phi_0,\Phi_1)$
has joint density
$(\Phi_0,\Phi_1)$
has joint density
with respect to
![]() $G\otimes G$
. Given
$G\otimes G$
. Given
![]() $\Phi_1=\phi_1$
, the random variable
$\Phi_1=\phi_1$
, the random variable
![]() $Z_1$
is exponentially distributed with mean
$Z_1$
is exponentially distributed with mean
![]() $\lambda(\phi_1)$
. Finally, as in the isotropic case, we have
$\lambda(\phi_1)$
. Finally, as in the isotropic case, we have
![]() $a(z_1)=\phi_1-\pi$
and so the random variable
$a(z_1)=\phi_1-\pi$
and so the random variable
![]() $\Phi_2$
has conditional density
$\Phi_2$
has conditional density
with respect to G, given
![]() $\Phi_1=\phi_1$
.
$\Phi_1=\phi_1$
.
With the same argument as in the isotropic case, we can now represent the triangle probability as follows:
 \begin{align*}p_3 &= \int_0^\pi\int_0^\pi\int_{\phi_1-\pi}^0\int_0^\infty \,\mathrm{e}^{-{(\lambda(\phi_2)z_2+\lambda(\phi_3)z_3-\lambda(\phi_1)z_1)}/{2}} \\ &\quad \times\dfrac{2}{ \sqrt{3}(p+q-p^2-q^2-pq)}\sin\!(\phi_0-\phi_1)\\&\quad \times\dfrac{1}{\lambda(\phi_1)}\sin\!(\phi_1-\phi_2)\times\lambda(\phi_1)\,\mathrm{e}^{-\lambda(\phi_1)z_1}\,\mathrm{d} z_1G(\mathrm{d} \phi_2)(G\otimes G)(\mathrm{d} (\phi_0,\phi_1))\\&= \int_0^\pi\int_0^\pi\int_{\phi_1-\pi}^0\int_0^\infty \,\mathrm{e}^{-{(\lambda(\phi_1)z_1+\lambda(\phi_2)z_2+\lambda(\phi_3)z_3)}/{2}}\,\times\dfrac{2}{ \sqrt{3}(p+q-p^2-q^2-pq)}\\ &\quad \times\sin\!(\phi_0-\phi_1)\sin\!(\phi_1-\phi_2)\,\mathrm{d} z_1G(\mathrm{d} \phi_2)(G\otimes G)(\mathrm{d} (\phi_0,\phi_1));\end{align*}
\begin{align*}p_3 &= \int_0^\pi\int_0^\pi\int_{\phi_1-\pi}^0\int_0^\infty \,\mathrm{e}^{-{(\lambda(\phi_2)z_2+\lambda(\phi_3)z_3-\lambda(\phi_1)z_1)}/{2}} \\ &\quad \times\dfrac{2}{ \sqrt{3}(p+q-p^2-q^2-pq)}\sin\!(\phi_0-\phi_1)\\&\quad \times\dfrac{1}{\lambda(\phi_1)}\sin\!(\phi_1-\phi_2)\times\lambda(\phi_1)\,\mathrm{e}^{-\lambda(\phi_1)z_1}\,\mathrm{d} z_1G(\mathrm{d} \phi_2)(G\otimes G)(\mathrm{d} (\phi_0,\phi_1))\\&= \int_0^\pi\int_0^\pi\int_{\phi_1-\pi}^0\int_0^\infty \,\mathrm{e}^{-{(\lambda(\phi_1)z_1+\lambda(\phi_2)z_2+\lambda(\phi_3)z_3)}/{2}}\,\times\dfrac{2}{ \sqrt{3}(p+q-p^2-q^2-pq)}\\ &\quad \times\sin\!(\phi_0-\phi_1)\sin\!(\phi_1-\phi_2)\,\mathrm{d} z_1G(\mathrm{d} \phi_2)(G\otimes G)(\mathrm{d} (\phi_0,\phi_1));\end{align*}
the term
![]() $\mathrm{e}^{-{(\lambda(\phi_2)z_2+\lambda(\phi_3)z_3-\lambda(\phi_1)z_1)}/{2}}$
represents the probability that after the stochastic construction of the typical triangle the random line process X
′′ does not intersect the two edges with lengths
$\mathrm{e}^{-{(\lambda(\phi_2)z_2+\lambda(\phi_3)z_3-\lambda(\phi_1)z_1)}/{2}}$
represents the probability that after the stochastic construction of the typical triangle the random line process X
′′ does not intersect the two edges with lengths
![]() $z_2$
and
$z_2$
and
![]() $z_2$
, whereas the other terms are the (conditional) densities of
$z_2$
, whereas the other terms are the (conditional) densities of
![]() $(\Phi_0,\Phi_1)$
,
$(\Phi_0,\Phi_1)$
,
![]() $\Phi_2$
, and
$\Phi_2$
, and
![]() $Z_1$
. From the discussion at the beginning of this section we know the three outer integrals are just a sum of two terms corresponding to the following angles:
$Z_1$
. From the discussion at the beginning of this section we know the three outer integrals are just a sum of two terms corresponding to the following angles:
 \begin{alignat*}{5}&\text{case 1}\quad &&\phi_0 =0,\quad &&\phi_1=\dfrac{\pi}{ 3},\quad &&\phi_2 =\dfrac{2\pi}{ 3},\quad &&\phi_3 =-\pi,\\ &\text{case 2}\quad &&\phi_0=\dfrac{\pi}{ 3},&&\phi_1=\dfrac{2\pi}{ 3},&&\phi_2 ={0},&&\phi_3 =-\dfrac{2\pi}{ 3}.\end{alignat*}
\begin{alignat*}{5}&\text{case 1}\quad &&\phi_0 =0,\quad &&\phi_1=\dfrac{\pi}{ 3},\quad &&\phi_2 =\dfrac{2\pi}{ 3},\quad &&\phi_3 =-\pi,\\ &\text{case 2}\quad &&\phi_0=\dfrac{\pi}{ 3},&&\phi_1=\dfrac{2\pi}{ 3},&&\phi_2 ={0},&&\phi_3 =-\dfrac{2\pi}{ 3}.\end{alignat*}
In both cases, using (3.1), we conclude that, given
![]() $\Phi_1=\phi_1$
,
$\Phi_1=\phi_1$
,
![]() $Z_1=z_1$
, and
$Z_1=z_1$
, and
![]() $\Phi_2=\phi_2$
, we have
$\Phi_2=\phi_2$
, we have
![]() $z_1=z_2=z_3$
, formally confirming that we are dealing with regular triangles. Moreover, in both cases we have
$z_1=z_2=z_3$
, formally confirming that we are dealing with regular triangles. Moreover, in both cases we have
![]() $\lambda(\phi_1)+\lambda(\phi_2)+\lambda(\phi_3) = \sqrt{3}$
, implying that
$\lambda(\phi_1)+\lambda(\phi_2)+\lambda(\phi_3) = \sqrt{3}$
, implying that
Hence
 \begin{align*}p_3 = \dfrac{2}{\sqrt{3}}&\times\dfrac{2}{ \sqrt{3}(p+q-p^2-q^2-pq)}\\ &\times\int_0^\pi\int_0^\pi\int_{\phi_1-\pi}^0\sin\!(\phi_0-\phi_1)\sin\!(\phi_1-\phi_2)\,G(\mathrm{d} \phi_2)(G\otimes G)(\mathrm{d} (\phi_0,\phi_1)).\end{align*}
\begin{align*}p_3 = \dfrac{2}{\sqrt{3}}&\times\dfrac{2}{ \sqrt{3}(p+q-p^2-q^2-pq)}\\ &\times\int_0^\pi\int_0^\pi\int_{\phi_1-\pi}^0\sin\!(\phi_0-\phi_1)\sin\!(\phi_1-\phi_2)\,G(\mathrm{d} \phi_2)(G\otimes G)(\mathrm{d} (\phi_0,\phi_1)).\end{align*}
Finally, in case 1, which has weight
![]() $pq(1-p-q)$
, the integrand equals
$pq(1-p-q)$
, the integrand equals
![]() $3/4$
, and in case 2, which has weight
$3/4$
, and in case 2, which has weight
![]() $p(1-p-q)p$
, the integrand equals
$p(1-p-q)p$
, the integrand equals
![]() $3/4$
as well. This eventually leads to
$3/4$
as well. This eventually leads to
and concludes the proof of the first part of Theorem 1.1.
For the second part, define the function
on the domain
![]() $D\,:\!=\, \{(p,q)\in(0,1)^2\,:\, 0<p+q<1\}$
whose gradient is
$D\,:\!=\, \{(p,q)\in(0,1)^2\,:\, 0<p+q<1\}$
whose gradient is
Solving
![]() ${\rm grad}F(p,q)=(0,0)$
leads to the only solution
${\rm grad}F(p,q)=(0,0)$
leads to the only solution
![]() $(p,q)=(1/3,1/3)$
on D. One can easily check that this is indeed the global maximum of F(p, q) on D. Since
$(p,q)=(1/3,1/3)$
on D. One can easily check that this is indeed the global maximum of F(p, q) on D. Since
![]() $p_3(G_3(1/3,1/3))=2/9$
, the proof of Theorem 1.1 is complete.
$p_3(G_3(1/3,1/3))=2/9$
, the proof of Theorem 1.1 is complete.
4.2. Triangle probability for three general directions: Proof of Corollary 1.1
Recall the definition of the directional distribution G from the statement of Corollary 1.1 and define the unit vectors
 \begin{alignat*}{5}v_1 & \,:\!=\, (0,1), &\quad v_2 &\,:\!=\, \biggl(\dfrac{1}{ 2},\dfrac{\sqrt{3}}{ 2}\biggr), &\quad v_3 &\,:\!=\, \biggl({-}\dfrac{1}{ 2},\dfrac{\sqrt{3}}{ 2}\biggr),\\w_1 &\,:\!=\, (\!\cos\varphi_1,\sin\varphi_1), & \quad w_2 &\,:\!=\, (\!\cos\varphi_2,\sin\varphi_2), &\quad w_3 &\,:\!=\, (\!\cos\varphi_3,\sin\varphi_3).\end{alignat*}
\begin{alignat*}{5}v_1 & \,:\!=\, (0,1), &\quad v_2 &\,:\!=\, \biggl(\dfrac{1}{ 2},\dfrac{\sqrt{3}}{ 2}\biggr), &\quad v_3 &\,:\!=\, \biggl({-}\dfrac{1}{ 2},\dfrac{\sqrt{3}}{ 2}\biggr),\\w_1 &\,:\!=\, (\!\cos\varphi_1,\sin\varphi_1), & \quad w_2 &\,:\!=\, (\!\cos\varphi_2,\sin\varphi_2), &\quad w_3 &\,:\!=\, (\!\cos\varphi_3,\sin\varphi_3).\end{alignat*}
Then we can find a non-degenerate affine map
![]() $A\,:\, \mathbb{R}^2\to\mathbb{R}^2$
which satisfies
$A\,:\, \mathbb{R}^2\to\mathbb{R}^2$
which satisfies
![]() $A(v_i)=w_i$
for
$A(v_i)=w_i$
for
![]() $i\in\{1,2,3\}$
. Applying A to a Poisson line tessellation X with intensity one and directional distribution
$i\in\{1,2,3\}$
. Applying A to a Poisson line tessellation X with intensity one and directional distribution
![]() $G_3(p,q)$
leads again to a Poisson line tessellation AX by the well-known mapping property of general Poisson processes. By definition of A, its directional distribution equals
$G_3(p,q)$
leads again to a Poisson line tessellation AX by the well-known mapping property of general Poisson processes. By definition of A, its directional distribution equals
![]() $G=AG_3(p,q)$
and the intensity is given by the determinant of A. Moreover, the application of A leaves invariant the number of vertices of each of the cells of X. As a consequence, the two tessellations X and AX have the same proportion of triangles. As this quantity only depends on the directional distribution and not on the intensity parameter, it follows that
$G=AG_3(p,q)$
and the intensity is given by the determinant of A. Moreover, the application of A leaves invariant the number of vertices of each of the cells of X. As a consequence, the two tessellations X and AX have the same proportion of triangles. As this quantity only depends on the directional distribution and not on the intensity parameter, it follows that
![]() $p_3(G_3(p,q))=p_3(G)$
.
$p_3(G_3(p,q))=p_3(G)$
.
4.3. Triangle probability in the case of
 $\boldsymbol{k}$
directions: Proof of Theorem 1.2
$\boldsymbol{k}$
directions: Proof of Theorem 1.2
Recall the construction of a typical triangle based on the random angles
![]() $\Phi_0,\Phi_1,\Phi_2$
and the random edge length
$\Phi_0,\Phi_1,\Phi_2$
and the random edge length
![]() $Z_1$
. Since the Poisson line tessellation with directional distribution
$Z_1$
. Since the Poisson line tessellation with directional distribution
![]() $G_k$
is
$G_k$
is
![]() $G_k$
-pseudo-isotropic, the initial angle
$G_k$
-pseudo-isotropic, the initial angle
![]() $\Phi_0$
is irrelevant and we can just take
$\Phi_0$
is irrelevant and we can just take
![]() $\Phi_0=0$
. Moreover, recall that
$\Phi_0=0$
. Moreover, recall that
![]() $\Phi_3=\Phi_0-\pi=-\pi$
. It is now a crucial observation that the stochastic construction described above leads to a triangle if and only if
$\Phi_3=\Phi_0-\pi=-\pi$
. It is now a crucial observation that the stochastic construction described above leads to a triangle if and only if
since the angle sum of a triangle is equal to
![]() $\pi$
and since we require the vertex
$\pi$
and since we require the vertex
![]() $v_1$
to be the lexicographically smallest vertex of the triangle. Moreover, for fixed
$v_1$
to be the lexicographically smallest vertex of the triangle. Moreover, for fixed
![]() $1\leq i\leq k-2$
each such triangle can be rotated by the angles
$1\leq i\leq k-2$
each such triangle can be rotated by the angles
![]() $0,{\pi/ k},\ldots,{(k-i-1)\pi/ k}$
to yield another admissible triangle.
$0,{\pi/ k},\ldots,{(k-i-1)\pi/ k}$
to yield another admissible triangle.
We now determine the distribution of the relevant random variables and start with
![]() $\Phi_1$
. According to (2.1) and using the identity for sums of sines in arithmetic progressions from [Reference Knapp7] (with
$\Phi_1$
. According to (2.1) and using the identity for sums of sines in arithmetic progressions from [Reference Knapp7] (with
![]() $a=0$
and
$a=0$
and
![]() $d=\pi/k$
there), we have
$d=\pi/k$
there), we have
 \begin{align*}\lambda(0) &= \int_0^\pi|\sin\!(\theta)|\,G_k(\mathrm{d} \theta) = \dfrac{1}{ k}\sum_{\ell=0}^{k-1}\sin\dfrac{\ell\pi}{ k} = \dfrac{1}{ k}\dfrac{\sin\frac{(k-1)\pi}{ 2k}}{\sin\frac{\pi}{ 2k}} = \dfrac{1}{ k}\cot\dfrac{\pi}{ 2k},\end{align*}
\begin{align*}\lambda(0) &= \int_0^\pi|\sin\!(\theta)|\,G_k(\mathrm{d} \theta) = \dfrac{1}{ k}\sum_{\ell=0}^{k-1}\sin\dfrac{\ell\pi}{ k} = \dfrac{1}{ k}\dfrac{\sin\frac{(k-1)\pi}{ 2k}}{\sin\frac{\pi}{ 2k}} = \dfrac{1}{ k}\cot\dfrac{\pi}{ 2k},\end{align*}
and because of
![]() $G_k$
-pseudo-isotropy we also have
$G_k$
-pseudo-isotropy we also have
![]() $\lambda({\pi/ k})=\cdots=\lambda({(k-1)\pi/ k})=\lambda(0)$
. Thus it follows from (2.3) that
$\lambda({\pi/ k})=\cdots=\lambda({(k-1)\pi/ k})=\lambda(0)$
. Thus it follows from (2.3) that
We can now conclude from (2.2) that the pair
![]() $(\Phi_0,\Phi_1)$
has joint density
$(\Phi_0,\Phi_1)$
has joint density
with respect to
![]() $G_k\otimes G_k$
. Integration with respect to
$G_k\otimes G_k$
. Integration with respect to
![]() $\phi_0$
now yields the marginal density
$\phi_0$
now yields the marginal density
of
![]() $\Phi_1$
with respect to
$\Phi_1$
with respect to
![]() $G_k$
, where
$G_k$
, where
 \begin{align*}\Sigma_k(\phi_1) \,:\!=\, \sum_{\substack{\phi_0\in\{0,{\pi}/{ k},\ldots,{((k-1)\pi)}/{ k}\}\\ \phi_0<\pi-\phi_1}}1. \end{align*}
\begin{align*}\Sigma_k(\phi_1) \,:\!=\, \sum_{\substack{\phi_0\in\{0,{\pi}/{ k},\ldots,{((k-1)\pi)}/{ k}\}\\ \phi_0<\pi-\phi_1}}1. \end{align*}
Note that
![]() $\Sigma_k(\phi_1)=k-\ell$
if
$\Sigma_k(\phi_1)=k-\ell$
if
![]() $\phi_1=\ell\pi/k$
for some
$\phi_1=\ell\pi/k$
for some
![]() $\ell\in\{0,\dots,k-1\}$
. The distribution of
$\ell\in\{0,\dots,k-1\}$
. The distribution of
![]() $Z_1$
is an exponential distribution with mean
$Z_1$
is an exponential distribution with mean
![]() $({\cot}\ \pi/ 2k)/k$
and so
$({\cot}\ \pi/ 2k)/k$
and so
![]() $Z_1$
has density
$Z_1$
has density
with respect to the Lebesgue measure. Finally, we deal with the conditional distribution of
![]() $\Phi_2$
given
$\Phi_2$
given
![]() $\Phi_1$
. As above, we have that the conditional density with respect to
$\Phi_1$
. As above, we have that the conditional density with respect to
![]() $G_k$
of
$G_k$
of
![]() $\Phi_2$
given
$\Phi_2$
given
![]() $\Phi_1=\phi_1$
equals
$\Phi_1=\phi_1$
equals
Since the integral in the denominator is just
![]() $\lambda(\phi_1)$
, we arrive at
$\lambda(\phi_1)$
, we arrive at
for the conditional density of
![]() $\Phi_2$
.
$\Phi_2$
.
As in the two previous sections, we can now express
![]() $p_3\,:\!=\, p_3(G_k)$
as follows:
$p_3\,:\!=\, p_3(G_k)$
as follows:
 \begin{align*}p_3 &= \int_0^\pi\int_{\phi_1-\pi}^0\int_0^\infty \dfrac{2\Sigma_k(\phi_1)}{\cot\frac{\pi}{ 2k}}\sin\!(\phi_1)\times \dfrac{1}{ k}\cot\dfrac{\pi}{ 2k} \,\exp\biggl({-\frac{1}{ k}\cot\frac{\pi}{ 2k}\,z_1}\biggr) \\ &\quad \times \dfrac{k}{\cot\frac{\pi}{ 2k}}\,\sin\!(\phi_1-\phi_2) \times \mathrm{e}^{-{(\lambda(\phi_2)z_2+\lambda(\phi_3)z_3-\lambda(\phi_1)z_1)}/{2}}\,\mathrm{d} z_1G_k(\mathrm{d} \phi_2)G_k(\mathrm{d} \phi_1)\\&= \dfrac{2}{\cot\frac{\pi}{ 2k}}\int_0^\pi\int_{\phi_1-\pi}^0 \Sigma_k(\phi_1)\sin\!(\phi_1)\sin\!(\phi_1-\phi_2)\\ &\quad \times\int_0^\infty \,\exp\biggl({-\frac{1}{ 2k}\cot\frac{\pi}{ 2k}(z_1+z_2+z_3)}\biggr)\,\mathrm{d} z_1G_k(\mathrm{d} \phi_2)G_k(\mathrm{d} \phi_1),\end{align*}
\begin{align*}p_3 &= \int_0^\pi\int_{\phi_1-\pi}^0\int_0^\infty \dfrac{2\Sigma_k(\phi_1)}{\cot\frac{\pi}{ 2k}}\sin\!(\phi_1)\times \dfrac{1}{ k}\cot\dfrac{\pi}{ 2k} \,\exp\biggl({-\frac{1}{ k}\cot\frac{\pi}{ 2k}\,z_1}\biggr) \\ &\quad \times \dfrac{k}{\cot\frac{\pi}{ 2k}}\,\sin\!(\phi_1-\phi_2) \times \mathrm{e}^{-{(\lambda(\phi_2)z_2+\lambda(\phi_3)z_3-\lambda(\phi_1)z_1)}/{2}}\,\mathrm{d} z_1G_k(\mathrm{d} \phi_2)G_k(\mathrm{d} \phi_1)\\&= \dfrac{2}{\cot\frac{\pi}{ 2k}}\int_0^\pi\int_{\phi_1-\pi}^0 \Sigma_k(\phi_1)\sin\!(\phi_1)\sin\!(\phi_1-\phi_2)\\ &\quad \times\int_0^\infty \,\exp\biggl({-\frac{1}{ 2k}\cot\frac{\pi}{ 2k}(z_1+z_2+z_3)}\biggr)\,\mathrm{d} z_1G_k(\mathrm{d} \phi_2)G_k(\mathrm{d} \phi_1),\end{align*}
where in the last step we used that
![]() $\lambda(\phi)=\lambda(0)$
for all angles
$\lambda(\phi)=\lambda(0)$
for all angles
![]() $\phi$
in the support of
$\phi$
in the support of
![]() $G_k$
.
$G_k$
.
To determine
![]() $z_2$
and
$z_2$
and
![]() $z_3$
we can use the law of sines as illustrated in Figure 8.
$z_3$
we can use the law of sines as illustrated in Figure 8.

Figure 8. Determination of
![]() $z_2$
and
$z_2$
and
![]() $z_3$
.
$z_3$
.
If
![]() $\phi_1={i\pi/ k}$
,
$\phi_1={i\pi/ k}$
,
![]() $1\leq i\leq n-2$
, and
$1\leq i\leq n-2$
, and
![]() $\phi_2=-{j\pi/ k}$
,
$\phi_2=-{j\pi/ k}$
,
![]() $1\leq j\leq n-i-1$
, this yields
$1\leq j\leq n-i-1$
, this yields
 \begin{align*}z_2 = z_1\dfrac{\sin\frac{i\pi}{ k}}{\sin\frac{j\pi}{ k}}\quad \text{and}\quad z_3 = z_1\dfrac{\sin\frac{{(i+j)}\pi}{ k}}{\sin\frac{j\pi}{ k}}.\end{align*}
\begin{align*}z_2 = z_1\dfrac{\sin\frac{i\pi}{ k}}{\sin\frac{j\pi}{ k}}\quad \text{and}\quad z_3 = z_1\dfrac{\sin\frac{{(i+j)}\pi}{ k}}{\sin\frac{j\pi}{ k}}.\end{align*}
Thus
 \begin{align*}&\dfrac{1}{ 2k}\cot\dfrac{\pi}{ 2k}(z_1+z_2+z_3) = \dfrac{1}{ 2k}\cot\dfrac{\pi}{ 2k}\dfrac{\sin\frac{i\pi}{ k}+\sin\frac{j\pi}{ k}+\sin\frac{(i+j)\pi}{ k}}{\sin\frac{j\pi}{ k}}z_1,\end{align*}
\begin{align*}&\dfrac{1}{ 2k}\cot\dfrac{\pi}{ 2k}(z_1+z_2+z_3) = \dfrac{1}{ 2k}\cot\dfrac{\pi}{ 2k}\dfrac{\sin\frac{i\pi}{ k}+\sin\frac{j\pi}{ k}+\sin\frac{(i+j)\pi}{ k}}{\sin\frac{j\pi}{ k}}z_1,\end{align*}
and the integral with respect to
![]() $z_1$
evaluates to
$z_1$
evaluates to
 \[\int_0^\infty \,\exp\biggl({-\frac{1}{ 2k}\cot\frac{\pi}{ 2k}(z_1+z_2+z_3)}\biggr)\,\mathrm{d} z_1=\dfrac{2k\sin\frac{j\pi}{ k}}{ \cot\frac{\pi}{ 2k}\big(\sin\frac{i\pi}{ k}+\sin\frac{j\pi}{ k}+\sin\frac{(i+j)\pi}{ k}\big)}.\]
\[\int_0^\infty \,\exp\biggl({-\frac{1}{ 2k}\cot\frac{\pi}{ 2k}(z_1+z_2+z_3)}\biggr)\,\mathrm{d} z_1=\dfrac{2k\sin\frac{j\pi}{ k}}{ \cot\frac{\pi}{ 2k}\big(\sin\frac{i\pi}{ k}+\sin\frac{j\pi}{ k}+\sin\frac{(i+j)\pi}{ k}\big)}.\]
Plugging this back into the expression for
![]() $p_3$
, we see that
$p_3$
, we see that
 \begin{align}p_3 &= \dfrac{4k}{\cot^2\frac{\pi}{ 2k}}\dfrac{1}{ k^2}\sum_{i=1}^{k-2}\Sigma_k\biggl(\dfrac{i\pi}{ k}\biggr)\sum_{j=1}^{k-i-1}\dfrac{\sin\frac{i\pi}{ k}\,\sin\frac{j\pi}{ k}\,\sin\frac{(i+j)\pi}{ k}}{ \sin\frac{i\pi}{k}+\sin\frac{j\pi}{ k}+\sin\frac{(i+j)\pi}{ k}}.\end{align}
\begin{align}p_3 &= \dfrac{4k}{\cot^2\frac{\pi}{ 2k}}\dfrac{1}{ k^2}\sum_{i=1}^{k-2}\Sigma_k\biggl(\dfrac{i\pi}{ k}\biggr)\sum_{j=1}^{k-i-1}\dfrac{\sin\frac{i\pi}{ k}\,\sin\frac{j\pi}{ k}\,\sin\frac{(i+j)\pi}{ k}}{ \sin\frac{i\pi}{k}+\sin\frac{j\pi}{ k}+\sin\frac{(i+j)\pi}{ k}}.\end{align}
Using
![]() $\Sigma_k({i\pi}/{ k})=k-i$
, we can complete the proof of Theorem 1.2.
$\Sigma_k({i\pi}/{ k})=k-i$
, we can complete the proof of Theorem 1.2.
4.4. The convergence to the isotropic case: Proof of Corollary 1.2
We start with the observation that
as
![]() $k\to\infty$
. Combining this with the representation for
$k\to\infty$
. Combining this with the representation for
![]() $p_3(G_k)$
in Theorem 1.2 implies
$p_3(G_k)$
in Theorem 1.2 implies
 \begin{align*}\lim_{k\to\infty} p_3(G_k) &= \lim_{k\to\infty} \dfrac{4}{ k}\tan^2\dfrac{\pi}{ 2k}\sum_{i=1}^{k-2}\Biggl[(k-i)\sum_{j=1}^{k-i-1}\dfrac{\sin\frac{i\pi}{ k}\,\sin\frac{j\pi}{ k}\,\sin\frac{(i+j)\pi}{ k}}{\sin\frac{i\pi}{ k}+\sin\frac{j\pi}{ k}+\sin\frac{(i+j)\pi}{ k}}\Biggr]\\ &= \lim_{k\to\infty} \dfrac{\pi^2}{k^3}\sum_{i=1}^{k-2}\Biggl[(k-i)\sum_{j=1}^{k-i-1}\dfrac{\sin\frac{i\pi}{ k}\,\sin\frac{j\pi}{ k}\,\sin\frac{(i+j)\pi}{ k}}{\sin\frac{i\pi}{ k}+\sin\frac{j\pi}{ k}+\sin\frac{(i+j)\pi}{ k}}\Biggr]\\ &= \lim_{k\to\infty} \pi^2\dfrac{1}{k}\sum_{i=1}^{k-2}\Biggl[\biggl(1-\dfrac{i}{k}\biggr)\dfrac{1}{k}\sum_{j=1}^{k-i-1}\dfrac{\sin\frac{i\pi}{ k}\,\sin\frac{j\pi}{ k}\,\sin\frac{(i+j)\pi}{ k}}{\sin\frac{i\pi}{ k}+\sin\frac{j\pi}{ k}+\sin\frac{(i+j)\pi}{ k}}\Biggr].\end{align*}
\begin{align*}\lim_{k\to\infty} p_3(G_k) &= \lim_{k\to\infty} \dfrac{4}{ k}\tan^2\dfrac{\pi}{ 2k}\sum_{i=1}^{k-2}\Biggl[(k-i)\sum_{j=1}^{k-i-1}\dfrac{\sin\frac{i\pi}{ k}\,\sin\frac{j\pi}{ k}\,\sin\frac{(i+j)\pi}{ k}}{\sin\frac{i\pi}{ k}+\sin\frac{j\pi}{ k}+\sin\frac{(i+j)\pi}{ k}}\Biggr]\\ &= \lim_{k\to\infty} \dfrac{\pi^2}{k^3}\sum_{i=1}^{k-2}\Biggl[(k-i)\sum_{j=1}^{k-i-1}\dfrac{\sin\frac{i\pi}{ k}\,\sin\frac{j\pi}{ k}\,\sin\frac{(i+j)\pi}{ k}}{\sin\frac{i\pi}{ k}+\sin\frac{j\pi}{ k}+\sin\frac{(i+j)\pi}{ k}}\Biggr]\\ &= \lim_{k\to\infty} \pi^2\dfrac{1}{k}\sum_{i=1}^{k-2}\Biggl[\biggl(1-\dfrac{i}{k}\biggr)\dfrac{1}{k}\sum_{j=1}^{k-i-1}\dfrac{\sin\frac{i\pi}{ k}\,\sin\frac{j\pi}{ k}\,\sin\frac{(i+j)\pi}{ k}}{\sin\frac{i\pi}{ k}+\sin\frac{j\pi}{ k}+\sin\frac{(i+j)\pi}{ k}}\Biggr].\end{align*}
Interpreting the two sums as Riemann sums with
![]() $i/k\to \mathrm{d} t$
and
$i/k\to \mathrm{d} t$
and
![]() $j/k\to \,\mathrm{d} s$
, as
$j/k\to \,\mathrm{d} s$
, as
![]() $k\to\infty$
, and noting that the condition
$k\to\infty$
, and noting that the condition
![]() $j\leq k-i-1$
asymptotically translates to
$j\leq k-i-1$
asymptotically translates to
![]() $s< 1-t$
, we conclude that
$s< 1-t$
, we conclude that
This, up to the substitutions
![]() $u=\pi t$
and
$u=\pi t$
and
![]() $v=-\pi s$
, is exactly the integral expression for
$v=-\pi s$
, is exactly the integral expression for
![]() $p_3(G_{\rm unif})$
we encountered already in (3.2). This completes the argument.
$p_3(G_{\rm unif})$
we encountered already in (3.2). This completes the argument.
5. Alternative proof of Miles’s result (1.1)
As mentioned in Section 1, it is known from [Reference Miles11] that
![]() $p_3(G_{\rm unif})=2-{\pi^2}/{6}$
. In this section, we use our Theorem 1.2 to give a ‘continuous-mapping-type’ argument leading to the same result. Our strategy is to prove that the weak convergence of
$p_3(G_{\rm unif})=2-{\pi^2}/{6}$
. In this section, we use our Theorem 1.2 to give a ‘continuous-mapping-type’ argument leading to the same result. Our strategy is to prove that the weak convergence of
![]() $G_k$
to
$G_k$
to
![]() $G_{\rm unif}$
implies the convergence of
$G_{\rm unif}$
implies the convergence of
![]() $p_3(G_k)$
to
$p_3(G_k)$
to
![]() $p_3(G_{\rm unif})$
, as
$p_3(G_{\rm unif})$
, as
![]() $k\to\infty$
. To conclude, we can then use Corollary 1.2, which shows that
$k\to\infty$
. To conclude, we can then use Corollary 1.2, which shows that
![]() $p_3(G_{\rm unif})=\lim_{k\to\infty}p_3(G_k)$
. The value of this limit is given by the integral (4.3), which has the value
$p_3(G_{\rm unif})=\lim_{k\to\infty}p_3(G_k)$
. The value of this limit is given by the integral (4.3), which has the value
![]() $2-{\pi^2}/{ 6}$
. The approach can be summarized in the following chain of equalities, in which
$2-{\pi^2}/{ 6}$
. The approach can be summarized in the following chain of equalities, in which
![]() $\lim^w$
stands for the weak limit of probability measures:
$\lim^w$
stands for the weak limit of probability measures:

To prove the first equality, we recall that the weak convergence of
![]() $G_k$
to
$G_k$
to
![]() $G_{\rm unif}$
implies the weak convergence of the product measures
$G_{\rm unif}$
implies the weak convergence of the product measures
![]() $G_k\otimes G_k\otimes G_k$
to
$G_k\otimes G_k\otimes G_k$
to
![]() $G_{\rm unif}\otimes G_{\rm unif}\otimes G_{\rm unif}$
; see [Reference Bogachev1, Proposition 2.7.7]. For each
$G_{\rm unif}\otimes G_{\rm unif}\otimes G_{\rm unif}$
; see [Reference Bogachev1, Proposition 2.7.7]. For each
![]() $k\geq 3$
, the triangle probability
$k\geq 3$
, the triangle probability
![]() $p_3(G_k)$
can be represented as the integral
$p_3(G_k)$
can be represented as the integral
with the function
![]() $f_k\,:\, [0,\pi)\times[0,\pi)\times[0,\pi)\to\mathbb{R}$
given by
$f_k\,:\, [0,\pi)\times[0,\pi)\times[0,\pi)\to\mathbb{R}$
given by
where
Note that if the integration with respect to
![]() $\phi_0$
is carried out, we arrive precisely at (4.1). It remains to observe that
$\phi_0$
is carried out, we arrive precisely at (4.1). It remains to observe that
![]() $4k^2\tan^2(\pi/2k)\to \pi^2$
as
$4k^2\tan^2(\pi/2k)\to \pi^2$
as
![]() $k\to\infty$
by (4.2) and that the function
$k\to\infty$
by (4.2) and that the function
![]() $(\phi_0,\phi_1,\phi_2)\mapsto T(\phi_0,\phi_1,\phi_2){\bf 1}\{\phi_0<\pi-\phi_1,\phi_1<\phi_2\}$
is bounded and
$(\phi_0,\phi_1,\phi_2)\mapsto T(\phi_0,\phi_1,\phi_2){\bf 1}\{\phi_0<\pi-\phi_1,\phi_1<\phi_2\}$
is bounded and
![]() $G_{\rm unif}\otimes G_{\rm unif}\otimes G_{\rm unif}$
-a.e. continuous on
$G_{\rm unif}\otimes G_{\rm unif}\otimes G_{\rm unif}$
-a.e. continuous on
![]() $[0,\pi)\times[0,\pi)\times[0,\pi)$
. The result thus follows from [Reference Bogachev1, Corollary 2.2.10].
$[0,\pi)\times[0,\pi)\times[0,\pi)$
. The result thus follows from [Reference Bogachev1, Corollary 2.2.10].
Acknowledgements
We are grateful to Tom Kaufmann and Daniel Rosen for inspiring ideas and constructive discussions on the subject of this paper. We also thank an Associate Editor and the referee for useful comments and remarks.
Funding information
CT was supported by the DFG priority programme SPP 2265 Random Geometric Systems.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.