Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-09T07:00:28.400Z Has data issue: false hasContentIssue false
  • English
  • Français

Products of distribution functions attracted to extreme value laws

Published online by Cambridge University Press:  14 July 2016

Sidney I. Resnick
Sidney I. Resnick*
Affiliation:
Technion—Israel Institute of Technology
Get access Rights & Permissions [Opens in a new window]

Abstract

When is the product of the d.f.'s H1(·), ···, Hm(·) attracted to an extreme value law φ(x)? We associate with each Hi(·) its A-function 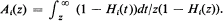Hi(x) is attracted to φ(x) if each Hi(x) is in the domain of attraction of φ(x) and Ai(z) ~ Aj(z), 1 ≦ i, j ≦ m. Equivalence of A-functions determines an equivalence relation which partitions the domain of attraction of φ(x)into one or more convex sets. These sets fail to be closed under passages to the limit (complete convergence).

Type
Research Papers
Information
Journal of Applied Probability , Volume 8 , Issue 4 , December 1971 , pp. 781 - 793
Copyright
Copyright © Applied Probability Trust 1971 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] De Haan, L. (1971) A form of regular variation and its application to the domain of attraction of the double exponential distribution. Z. Wahrscheinlichkeitsth. 17, 241–258.CrossRefGoogle Scholar
[2] De Haan, L. (1970) On Regular Variation and its Application to Weak Convergence of Sample Extremes. Mathematical Center Tracts 32, Amsterdam.Google Scholar
[3] De Haan, L. and Balkema, A. A. (1971) On R. Von Mises condition for the domain of attraction of exp{—e–x}. Report SW 10/71, Mathematical Center, Amsterdam.Google Scholar
[4] Feller, W. (1966) An Introduction to Probability Theory and its Applications. Vol. 2, Wiley, New York.Google Scholar
[5] Gnedenko, B. V. (1943) Sur la distribution limite du terme maximum d'une série aléatoire. Ann. Math. 44, 423–453.Google Scholar
[6] Kolmogorov, A. N. and Gnedenko, B. V. (1954) Limit Distributions for Sums of Independent Random Variables. Addison-Wesley, Massachusetts.Google Scholar
[7] Marcus, M. and Pinsky, M. (1969) On the domain of attraction of exp{—e–x} J. Math. Anal. Appl. 28, 440–449.Google Scholar
[8] Resnick, S. I. (1971) Tail equivalence and its applications. J. Appl. Prob. 8, 136–156.CrossRefGoogle Scholar
[9] Resnick, S. I. and Neuts, M. F. (1969) Limit laws for maxima of a sequence of random variables defined on a Markov chain. Adv. Appl. Prob. 2, 323–343.Google Scholar
[10] Von Mises, R. (1936) La distribution de la plus grande de n valeurs. Selected Papers II (Amer. Math. Soc.) 271–294.Google Scholar