Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-05T21:24:09.830Z Has data issue: false hasContentIssue false
  • English
  • Français

A process with chain dependent growth rate

Published online by Cambridge University Press:  14 July 2016

Julian Keilson  and
S. Subba Rao
Julian Keilson
Affiliation:
University of Rochester, Rochester, New York
S. Subba Rao
Affiliation:
University of Rochester, Rochester, New York
Get access Rights & Permissions [Opens in a new window]

Extract

Additive processes on finite Markov chains have been investigated by Miller ([8], [9]), Keilson and Wishart ([2], [3], [4]) and by Fukushima and Hitsuda [1]. These papers study a two-dimensional Markov Process {X(t), R(t)} whose state space is R1 × {1, 2, ···, R} characterized by the following properties:

  1. (i) R(t) is an irreducible Markov chain on states 1,2, …,R governed by atransition probability matrix Bo = {brs}.

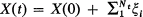  2. (ii) X(t) is a sum of random increments dependent on the chain, i.e., if the ith transition takes the chain from state r to state s, then the increment 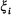has the distribution

  3. (iii) Nt, is t in discrete time while in the continuous time case Nt, might be an independent Poisson process.

Type
Research Papers
Information
Journal of Applied Probability , Volume 7 , Issue 3 , December 1970 , pp. 699 - 711
Copyright
Copyright © Applied Probability Trust 1970 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Fukushima, M. and Hitsuda, M. (1967) On a class of Markov processes taking values on lines and the central limit theorem. Nagoya Math. J. 30, 47–56.CrossRefGoogle Scholar
[2] Keilson, J. and Wishart, D. M. G. (1964) A central limit theorem for processes defined on a finite Markov chain. Proc. Camb. Phil. Soc. 60, 547–567.CrossRefGoogle Scholar
[3] Keilson, J. and Wishart, D. M. G. (1965) Boundary problems for additive processes defined on a finite Markov chain. Proc. Camb. Phil. Soc. 61, 173–190.CrossRefGoogle Scholar
[4] Keilson, J. and Wishart, D. M. G. (1967) Addenda to processes defined on a finite Markov chain. Proc. Camb. Phil. Soc. 63, 187–193.CrossRefGoogle Scholar
[5] Keilson, J. (1965) A review of transient behavior in regular diffusion and birth-death processes–Part II. J. Appl. Prob. 2, 405–428.CrossRefGoogle Scholar
[6] Keilson, J. (1969) An intermittent channel with finite storage. Opsearch (India) 6, 109–117.Google Scholar
[7] Kemeny, J. G. and Snell, J. L. (1960) Finite Markov Chains. Van Nostrand, Princeton, N.J.Google Scholar
[8] Miller, H. D. (1961) A convexity property in the theory of random variables defined on a finite Markov chain. Ann. Math. Statist. 32, 1260–1270.CrossRefGoogle Scholar
[9] Miller, H. D. (1962) Absorption probabilities for sums of random variables defined on a finite Markov chain. Proc. Camb. Phil. Soc. 58, 286–298.CrossRefGoogle Scholar
[10] Miller, R. G. (1963) Continuous time stochastic storage processes with random linear inputs and outputs. J. Math. Mech. 12, 275–291.Google Scholar