Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T17:18:01.708Z Has data issue: false hasContentIssue false
  • English
  • Français

The probabilities of extinction in a branching random walk on a strip

Part of: Markov processes

Published online by Cambridge University Press:  04 September 2020

Peter Braunsteins  and
Sophie Hautphenne
Peter Braunsteins*
Affiliation:
The University of Melbourne
Sophie Hautphenne*
Affiliation:
The University of Melbourne
*
*Postal address: School of Mathematics and Statistics, The University of Melbourne, 3010, Melbourne, Australia.
*Postal address: School of Mathematics and Statistics, The University of Melbourne, 3010, Melbourne, Australia.
Get access Rights & Permissions [Opens in a new window]

Abstract

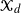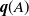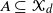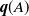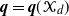We consider a class of multitype Galton–Watson branching processes with a countably infinite type set $\mathcal{X}_d$ whose mean progeny matrices have a block lower Hessenberg form. For these processes, we study the probabilities $\textbf{\textit{q}}(A)$ of extinction in sets of types $A\subseteq \mathcal{X}_d$ . We compare $\textbf{\textit{q}}(A)$ with the global extinction probability $\textbf{\textit{q}} = \textbf{\textit{q}}(\mathcal{X}_d)$ , that is, the probability that the population eventually becomes empty, and with the partial extinction probability 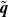$\tilde{\textbf{\textit{q}}}$ , that is, the probability that all types eventually disappear from the population. After deriving partial and global extinction criteria, we develop conditions for 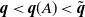$\textbf{\textit{q}} < \textbf{\textit{q}}(A) < \tilde{\textbf{\textit{q}}}$ . 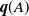We then present an iterative method to compute the vector $\textbf{\textit{q}}(A)$ for any set A. Finally, we investigate the location of the vectors 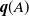$\textbf{\textit{q}}(A)$ in the set of fixed points of the progeny generating vector.

Keywords

Infinite-type branching processextinction probabilityfixed point

MSC classification

Primary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Secondary: 60J05: Discrete-time Markov processes on general state spaces 60J22: Computational methods in Markov chains
Type
Research Papers
Information
Journal of Applied Probability , Volume 57 , Issue 3 , September 2020 , pp. 811 - 831
Check for updates
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bertacchi, D. and Zucca, F. (2014). Strong local survival of branching random walks is not monotone. Adv. Appl. Prob. 46, 400–421.10.1239/aap/1401369700CrossRefGoogle Scholar
Bertacchi, D. and Zucca, F. (2017). A generating function approach to branching random walks. Brazil. J. Prob. Statist. 31, 229–253.CrossRefGoogle Scholar
Biggins, J. D., Lubachevsky, B. D., Shwartz, A. and Weiss, A. (1991). A branching random walk with a barrier. Ann. Appl. Prob. 1, 573–581.CrossRefGoogle Scholar
Blackwell, D. (1955). On transient Markov processes with a countable number of states and stationary transition probabilities. Ann. Math. Statist. 26, 654–658.10.1214/aoms/1177728425CrossRefGoogle Scholar
Bolthausen, E. and Goldsheid, I. (2000). Recurrence and transience of random walks in random environments on a strip. Commun. Math. Phys. 214, 429–447.10.1007/s002200000279CrossRefGoogle Scholar
Braunsteins, P., Decrouez, G. and Hautphenne, S. (2019). A pathwise approach to the extinction of branching processes with countably many types. Stoch. Process. Appl. 129, 713–739.10.1016/j.spa.2018.03.013CrossRefGoogle Scholar
Braunsteins, P. and Hautphenne, S. (2019). Extinction in lower Hessenberg branching processes with countably many types. Ann. Appl. Prob. 29, 2782–2818.10.1214/19-AAP1464CrossRefGoogle Scholar
Dolgopyat, D., Hebbar, P., Koralov, L. and Perlman, M. (2018). Multi-type branching processes with time-dependent branching rates. J. Appl. Prob. 55, 701–727.10.1017/jpr.2018.46CrossRefGoogle Scholar
Gantert, N., Müller, S., Popov, S. and Vachkovskaia, M. (2010). Survival of branching random walks in random environment. J. Theoret. Prob. 23, 1002–1014.10.1007/s10959-009-0227-5CrossRefGoogle Scholar
Harris, T. E. (1963). The Theory of Branching Processes. Springer, Berlin.CrossRefGoogle Scholar
Hautphenne, S., Latouche, G. and Nguyen, G. T. (2013). Extinction probabilities of branching processes with countably infinitely many types. Adv. Appl. Prob. 45, 1068–1082.10.1239/aap/1386857858CrossRefGoogle Scholar
Jones, O. D. (1997). On the convergence of multitype branching processes with varying environments. Ann. Appl. Prob. 7, 772–801.Google Scholar
Kimmel, M. and Axelrod, M. E. (2002). Branching Processes in Biology. Springer, New York.Google Scholar
Latouche, G. and Ramaswami, V. (1999). Introduction to Matrix Analytic Methods in Stochastic Modeling. Society for Industrial and Applied Mathematics, Philadelphia.10.1137/1.9780898719734CrossRefGoogle Scholar
Moyal, J. E. (1962). Multiplicative population chains. Proc. R. Soc. London A 266, 518–526.Google Scholar
Sagitov, S. (2013). Linear-fractional branching processes with countably many types. Stoch. Process. Appl. 123, 2940–2956.10.1016/j.spa.2013.03.008CrossRefGoogle Scholar
Seneta, E. (2006). Non-negative Matrices and Markov Chains. Springer, New York.Google Scholar
Spataru, A. (1989). Properties of branching processes with denumerably many types. Romanian J. Pure Appl. Math. 34, 747–759.Google Scholar
van Doorn, E. (2018). Asymptotic period of an aperiodic Markov chain. Markov Process. Relat. Fields 24, 759–778.Google Scholar
Zucca, F. (2011). Survival, extinction and approximation of discrete-time branching random walks. J. Statist. Phys. 142, 726–753.CrossRefGoogle Scholar