Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
López-Mimbela, José Alfredo
Birkner, Matthias
and
Wakolbinger, Anton
2005.
Comparison results and steady states for the Fujita equation with fractional Laplacian.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 22,
Issue. 1,
p.
83.
López-Mimbela, José Alfredo
and
Privault, Nicolas
2005.
Blow-up and stability of semilinear PDEs with gamma generators.
Journal of Mathematical Analysis and Applications,
Vol. 307,
Issue. 1,
p.
181.
Dascaliuc, Radu
Pham, Tuan N.
Thomann, Enrique
and
Waymire, Edward C.
2023.
Doubly stochastic Yule cascades (Part I): The explosion problem in the time-reversible case.
Journal of Functional Analysis,
Vol. 284,
Issue. 1,
p.
109722.


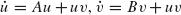 remain bounded for suitable bounded initial conditions, provided
remain bounded for suitable bounded initial conditions, provided 