Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T05:27:03.015Z Has data issue: false hasContentIssue false
  • English
  • Français

Physical nearest-neighbour models and non-linear time-series: III Non-zero means and sub-critical temperatures

Published online by Cambridge University Press:  14 July 2016

M. S. Bartlett
M. S. Bartlett*
Affiliation:
University of Oxford
Get access Rights & Permissions [Opens in a new window]

Abstract

The product moment equations previously derived are first discussed for the infinite one- and two-dimensional Ising (or autologistic) model in the case of non-zero mean, as a prelude to an examination of the probability structure in the higher-dimensional (and nominally zero mean) case below the ‘critical temperature’. Of two simple possible models, A and B, both consistent with the division of the product moment p into ergodic, and long-range non-ergodic, components, such that ρ = r (1 – m2) + m2, where r is the intrinsic correlation coefficient, it is shown that the second model B appears appropriate to the three-dimensional ‘spherical model’, but the first model A to the Ising model. Model A is defined by xi = yi + M, where M = +m or –m, and E{yi} = 0; and Model B by

Keywords

NEAREST-NEIGHBOUR LATTICE MODELSAUTO-LOGISTIC MODEL WITH NON-ZERO MEANISING MODEL AT SUB-CRITICAL TEMPERATURES
Type
Research Papers
Information
Journal of Applied Probability , Volume 11 , Issue 4 , December 1974 , pp. 715 - 725
Copyright
Copyright © Applied Probability Trust 1974 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

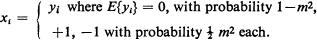
This paper was written while the author was a Visiting Fellow at the Australian National University, Canberra.

References

Bartlett, M. S. (1966) Stochastic Processes. 2nd ed. Cambridge University Press.Google Scholar
Bartlett, M. S. (1971) Physical nearest-neighbour models and non-linear time-series. J. Appl. Prob. 8, 222–232.Google Scholar
Bartlett, M. S. (1972) Physical nearest-neighbour models and non-linear time series II. J. Appl. Prob. 9, 76–86.Google Scholar
Bartlett, M. S. (1974) The statistical analysis of spatial pattern. Adv. Appl. Prob. 6, 336–358.Google Scholar
Berlin, T. H. and Kac, M. (1952) The spherical model of a ferromagnet. Phys. Rev. 86, 821–835.Google Scholar
Besag, J. E. (1972) Nearest-neighbour systems and the auto-logistic model for binary data. J. R. Statist. Soc. B 34, 73–83.Google Scholar
Besag, J. E. (1974) Spatial interaction and the statistical analysis of lattice systems. J. R. Statist. Soc. B 00, 000–000.Google Scholar
Dobrushin, R. L. (1968) The description of a random field by means of its conditional probabilities. Theor. Probability Appl. 13, 197–244.Google Scholar
Newell, G. F. and Montroll, E. W. (1953) On the theory of the Ising model of ferromagnetism. Rev. Modern Phys. 25, 353–389.Google Scholar
Spitzer, F. (1971) Markov random fields and Gibbs ensembles. Amer. Math. Monthly 78, 142–154.Google Scholar
Yang, C. N. (1952) The spontaneous magnetization of a two-dimensional Ising model. Phys. Rev. 85, 809–816.Google Scholar