Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Park, C.
1985.
Boundaries with negative jumps for the Brownian motion.
Journal of Applied Probability,
Vol. 22,
Issue. 04,
p.
964.


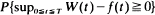 are well known. The main purpose of this paper is to present ways of finding barrier-absorption probabilities when the barrier function is defined only on sub-intervals of [0,
are well known. The main purpose of this paper is to present ways of finding barrier-absorption probabilities when the barrier function is defined only on sub-intervals of [0, 