Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T06:02:34.964Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimality of the one step look-ahead stopping times

Published online by Cambridge University Press:  14 July 2016

M. Abdel-Hameed
M. Abdel-Hameed*
Affiliation:
University of North Carolina at Charlotte
Get access Rights & Permissions [Opens in a new window]

Abstract

The optimality of the one step look-ahead stopping rule is shown to hold under conditions different from those discussed by Chow, Robbins and Seigmund [5]. These results are corollaries of the following theorem: Let {Xn, n = 0, 1, …}; X0 = x be a discrete-time homogeneous Markov process with state space (E, ℬ). For any ℬ-measurable function g and α in (0, 1], define Aαg(x) = αExg(X1) – g(x) to be the infinitesimal generator of g. If τ is any stopping time satisfying the conditions: Ex[αNg(XN)I(τ > N)]→0 as 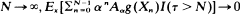as N → ∞, then 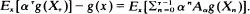Applications of the results are considered.

Keywords

OPTIMAL STOPPING TIMESMARKOV TIMESDISCRETE-TIME HOMOGENEOUS MARKOV PROCESSESNON-HOMOGENEOUS MARKOV PROCESSESINCREASING FUNCTIONSROOT-INCREASING FUNCTIONSINFINITESIMAL GENERATORS
Type
Research Papers
Information
Journal of Applied Probability , Volume 14 , Issue 1 , March 1977 , pp. 162 - 169
Copyright
Copyright © Applied Probability Trust 1977 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Abdel-Hameed, M. S. and Proschan, F. (1973) Non-stationary shock models. Stoch. Proc. Appl. 1, 383–404.Google Scholar
[2] Abdel-Hameed, M. S. and Proschan, F. (1975) Shock models with underlying birth process. J. Appl. Prob. 12, 18–28.Google Scholar
[3] Abdel-Hameed, M. S. and Proschan, F. (1975) Total positivity properties of generating functions. SIAM J. Math. Anal. 6, 81–84.Google Scholar
[4] Abdel-Hameed, M. S. and Proschan, F. (1976) Preservation of geometric properties under an integral transformation SIAM J. Math. Anal. 7, 359–365.Google Scholar
[5] Chow, Y. S., Robbins, H. and Seigmund, D. (1971) Great Expectations: The Theory of Optimal Stopping. Houghton Mifflin Company, Boston.Google Scholar
[6] Chung, K. L. (1974) A Course in Probability Theory. Academic Press, New York.Google Scholar
[7] Dynkin, E. B. (1965) Markov Processes. (English translation) Springer-Verlag, Berlin.Google Scholar
[8] Sirjaev, A. N. (1973) Statistical Sequential Analysis. (English translation) American Mathematical Society, Providence, R.I. Google Scholar