Article contents
Optimal coupling of jumpy Brownian motion on the circle
Published online by Cambridge University Press: 04 July 2023
Abstract
Consider a Brownian motion on the circumference of the unit circle, which jumps to the opposite point of the circumference at incident times of an independent Poisson process of rate 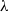 $\lambda$. We examine the problem of coupling two copies of this ‘jumpy Brownian motion’ started from different locations, so as to optimise certain functions of the coupling time. We describe two intuitive co-adapted couplings (‘Mirror’ and ‘Synchronous’) which differ only when the two processes are directly opposite one another, and show that the question of which strategy is best depends upon the jump rate
$\lambda$. We examine the problem of coupling two copies of this ‘jumpy Brownian motion’ started from different locations, so as to optimise certain functions of the coupling time. We describe two intuitive co-adapted couplings (‘Mirror’ and ‘Synchronous’) which differ only when the two processes are directly opposite one another, and show that the question of which strategy is best depends upon the jump rate 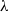 $\lambda$ in a non-trivial way. We also provide an explicit description of a (non-co-adapted) maximal coupling for any jump rate in the case that the two jumpy Brownian motions begin at antipodal points of the circle.
$\lambda$ in a non-trivial way. We also provide an explicit description of a (non-co-adapted) maximal coupling for any jump rate in the case that the two jumpy Brownian motions begin at antipodal points of the circle.
Keywords
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust
References
- 1
- Cited by



