Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T05:09:49.222Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal control of a finite dam using PMλΤ policies and penalty cost: total discounted and long run average cases

Published online by Cambridge University Press:  14 July 2016

M. Abdel-hameed  and
Y. Nakhi
M. Abdel-hameed*
Affiliation:
University of Kuwait
Y. Nakhi
Affiliation:
University of Kuwait
*
∗ Postal address for both authors: Department of Statistics and Operations Research, Kuwait University, College of Science, P.O. Box 5969, Kuwait.
Get access Rights & Permissions [Opens in a new window]

Abstract

Zuckermann [10] considers the problem of optimal control of a finite dam using 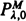policies, assuming that the input process is Wiener with drift term μ ≧ 0. Lam Yeh and Lou Jiann Hua [7] treat the case where the input is a Wiener process with a reflecting boundary at zero, with drift term μ ≧ 0, using the long-run average cost and total discounted cost criteria. Attia [1] obtains results similar to those of Lam Yeh and Lou Jiann Hua for the long-run average case and extends them to include μ < 0. In this paper we look further into the results of Zuckerman [10], simplify some of the work of Attia [1], [2], offering corrections to some of his formulae and extend the results of Lam Yeh and Lou Jiann Hua [7].

Keywords

WIENER INPUTDRIFTREFLECTING BOUNDARYGEOMETRIC WIENER INPUT
Type
Research Papers
Information
Journal of Applied Probability , Volume 27 , Issue 4 , December 1990 , pp. 888 - 898
Copyright
Copyright © Applied Probability Trust 1990 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

∗

Research supported by Kuwait University Grant SM064. Research partly carried out while this author was at the University of North Carolina.

References

[1] Attia, F. A. (1987) The control of a finite dam with penalty cost function: Wiener process input. Stoch. Proc. Appl. 25, 289–299.Google Scholar
[2] Attia, F. A. (1989) Resolvent operators of Markov processes and their applications in the control of a finite dam. J. Appl. Prob. 26, 314–324.Google Scholar
[3] Blumenthal, R. M. and Getoor, R. K. (1968) Markov Process and Potential Theory. Academic Press, New York.Google Scholar
[4] Harrison, J. M. (1985) Brownian Motion and Stochastic Flow System. Wiley, New York.Google Scholar
[5] Karlin, S. and Taylor, H. W. (1975) A First Course In Stochastic Processes. Academic Press, New York.Google Scholar
[6] Karlin, S. and Taylor, H. W. (1981) A Second Course In Stochastic Processes. Academic Press, New York.Google Scholar
[7] Yeh, Lam and Hua, Lou Jiann (1987) Optimal control of a finite dam. J. Appl. Prob. 24, 186–199.Google Scholar
[8] Lamperti, J. (1977) Stochastic Processes: A Survey of the Mathematical Theory. Springer-Verlag, New York.Google Scholar
[9] Oberhettinger, F. (1977) Tables of Mellin Transforms. Springer-Verlag, Berlin.Google Scholar
[10] Zuckerman, D. (1977) Two-stage output procedure of a finite dam. J. Appl. Prob. 14, 421–425.Google Scholar