Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kalpazidou, S.
1992.
Circuit processes and the corresponding one-parameter semigroup of weight operators.
Journal of Theoretical Probability,
Vol. 5,
Issue. 1,
p.
205.
Kalpazidou, S.
1993.
On Levy's theorem concerning positiveness of transition probabilities of Markov processes: the circuit processes case.
Journal of Applied Probability,
Vol. 30,
Issue. 01,
p.
28.
Kalpazidou, S.
1995.
Circuit duality for recurrent Markov processes.
Circuits Systems and Signal Processing,
Vol. 14,
Issue. 2,
p.
187.
Satinover, J. B.
and
Sornette, D.
2012.
Cycles, determinism and persistence in agent-based games and financial time-series: part II.
Quantitative Finance,
Vol. 12,
Issue. 7,
p.
1065.


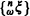 whose finite distributions depend upon the sample paths
whose finite distributions depend upon the sample paths 