Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T23:03:25.105Z Has data issue: false hasContentIssue false
  • English
  • Français

On the validity of Wald's equation

Part of: Stochastic processes

Published online by Cambridge University Press:  14 July 2016

Markus Roters
Markus Roters*
Affiliation:
Universität Trier
*
∗Postal address: FB IV Mathematik/Statistik, Universität Trier, D-54286 Trier, Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we review conditions under which Wald's equation holds, mainly if the expectation of the given stopping time is infinite. As a main result we obtain what is probably the weakest possible version of Wald's equation for the case of independent, identically distributed (i.i.d.) random variables. Moreover, we improve a result of Samuel (1967) concerning the existence of stopping times for which the expectation of the stopped sum of the underlying i.i.d. sequence of random variables 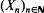does not exist. Finally, we show by counterexamples that it is impossible to generalize a theorem of Kiefer and Wolfowitz (1956) relating the moments of the supremum of a random walk 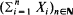with negative drift to moments of the positive part of X1 to the case where the expectation of X1 is —∞. Here, the Laplace–Stieltjes transform of the supremum of the considered random walk plays an important role.

Keywords

LAPLACE–STIELTJES TRANSFORMMARTINGALEOPTIMAL STOPPINGRANDOMIZED STOPPING TIMESTABLE LAWSUPREMUM OF A RANDOM WALK

MSC classification

Primary: 60G40: Stopping times; optimal stopping problems; gambling theory
Secondary: 60G50: Sums of independent random variables; random walks
Type
Research Article
Information
Journal of Applied Probability , Volume 31 , Issue 4 , December 1994 , pp. 949 - 957
Copyright
Copyright © Applied Probability Trust 1994 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blackwell, D. (1946) On an equation of Wald. Ann. Math . Statist. 17, 84–87.Google Scholar
Brown, B. M. (1969) Moments of a stopping rule related to the central limit theorem. Ann. Math. Statist. 40, 1236–1249.CrossRefGoogle Scholar
Chow, Y. S. and Lai, T. L. (1979) On the maximal excess in boundary crossings of random walks related to fluctuation theory and laws of large numbers. Bull. Inst. Math. Acad. Sinica 7, 271–289.Google Scholar
Chow, Y. S. and Teicher, H. (1978) Probability Theory, Independence, Interchangeability, Martingales . Springer-Verlag, New York.Google Scholar
Chow, Y. S., Robbins, H. and Siegmund, D. (1971) Great Expectations: The Theory of Optimal Stopping. Houghton Mifflin, Boston.Google Scholar
Feller, W. (1971) An Introduction to Probability Theory and its Applications , Vol. II, 2nd ed. Wiley, New York.Google Scholar
Gut, A. (1988) Randomly Stopped Sums, Limit Theorems and Applications. Springer-Verlag, New York.Google Scholar
Kiefer, J. and Wolfowitz, J. (1956) On the characteristics of the general queueing process, with applications to random walk. Ann. Math. Statist. 27, 147–161.CrossRefGoogle Scholar
Klass, M. J. (1988) A best possible improvement of Wald's equation. Ann. Prob. 16, 840–853.CrossRefGoogle Scholar
Loeve, ?. (1977) Probability Theory I, 4th ed. Springer-Verlag, New York.Google Scholar
Robbins, H. and Samuel, E. (1966) An extension of a lemma of Wald. J. Appl. Prob. 3, 272–273.CrossRefGoogle Scholar
Samuel, E. (1967) On the existence of the expectation of randomly stopped sums. J. Appl. Prob. 4, 197–200.CrossRefGoogle Scholar
Taylor, ?. ?. (1972) Bounds for stopped partial sums. Ann. Math. Statist. 43, 733–747.CrossRefGoogle Scholar
Veraverbeke, N. (1977) Asymptotic behaviour of Wiener-Hopf factors of a random walk. Stoch. Proc. Appl. 5, 27–37.CrossRefGoogle Scholar
Wald, A. (1945) Sequential tests of statistical hypotheses. Ann. Math. Statist. 16, 117–186.Google Scholar