Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Orsingher, Enzo
and
Bassan, Bruno
1989.
On the comparison of the distribution of the supremum of random fields represented by stochastic integrals.
Advances in Applied Probability,
Vol. 21,
Issue. 4,
p.
770.


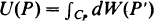 , where
, where 