Article contents
On the integral of the workload process of the single server queue
Published online by Cambridge University Press: 14 July 2016
Abstract
This paper is devoted to a study of the integral of the workload process of the single server queue, in particular during one busy period. Firstly, we find asymptotics of the area 𝒜 swept under the workload process W(t) during the busy period when the service time distribution has a regularly varying tail. We also investigate the case of a light-tailed service time distribution. Secondly, we consider the problem of obtaining an explicit expression for the distribution of 𝒜. In the general GI/G/1 case, we use a sequential approximation to find the Laplace—Stieltjes transform of 𝒜. In the M/M/1 case, this transform is obtained explicitly in terms of Whittaker functions. Thirdly, we consider moments of 𝒜 in the GI/G/1 queue. Finally, we show asymptotic normality of 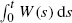 .
.
Keywords
MSC classification
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 2003
Footnotes
Work supported by KBN under grant 5 P03A 02120
References
- 10
- Cited by


