Article contents
On sequential occupancy problems
Published online by Cambridge University Press: 14 July 2016
Abstract
Consider n cells into which balls are thrown at random until k cells contain at least l + 1 balls each. Let Yl, · ··, Yn be the number of balls in the cells when stopping. In this paper two representations are given for the characteristic functions of random variables of the form 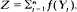 The usefulness of these representations are illustrated by two examples. In the first the number of cells with exactly one ball when each cell contains at least one ball is considered. In the second the waiting time until the ball-throwing process stops is discussed.
The usefulness of these representations are illustrated by two examples. In the first the number of cells with exactly one ball when each cell contains at least one ball is considered. In the second the waiting time until the ball-throwing process stops is discussed.
Keywords
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust
Footnotes
Research supported by a fellowship from the American-Scandinavian Foundation and a grant from the Swedish Natural Science Research Council. The work was partly carried out while the author was visiting Stanford University.
References
- 8
- Cited by


