Published online by Cambridge University Press: 22 November 2021
Consider a homogeneous Poisson point process of the Euclidean plane and its Voronoi tessellation. The present note discusses the properties of two stationary point processes associated with the latter and depending on a parameter 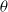 $\theta$
. The first is the set of points that belong to some one-dimensional facet of the Voronoi tessellation and such that the angle with which they see the two nuclei defining the facet is
$\theta$
. The first is the set of points that belong to some one-dimensional facet of the Voronoi tessellation and such that the angle with which they see the two nuclei defining the facet is 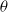 $\theta$
. The main question of interest on this first point process is its intensity. The second point process is that of the intersections of the said tessellation with a straight line having a random orientation. Its intensity is well known. The intersection points almost surely belong to one-dimensional facets. The main question here concerns the Palm distribution of the angle with which the points of this second point process see the two nuclei associated with the facet. We will give answers to these two questions and briefly discuss their practical motivations. We also discuss natural extensions to three dimensions.
$\theta$
. The main question of interest on this first point process is its intensity. The second point process is that of the intersections of the said tessellation with a straight line having a random orientation. Its intensity is well known. The intersection points almost surely belong to one-dimensional facets. The main question here concerns the Palm distribution of the angle with which the points of this second point process see the two nuclei associated with the facet. We will give answers to these two questions and briefly discuss their practical motivations. We also discuss natural extensions to three dimensions.