Article contents
On Λ-Fleming–Viot processes with general frequency-dependent selection
Published online by Cambridge University Press: 23 November 2020
Abstract
We construct a multitype constant-size population model allowing for general selective interactions as well as extreme reproductive events. Our multidimensional model aims for the generality of adaptive dynamics and the tractability of population genetics. It generalises the idea of Krone and Neuhauser [39] and González Casanova and Spanò [29], who represented the selection by allowing individuals to sample several potential parents in the previous generation before choosing the ‘strongest’ one, by allowing individuals to use any rule to choose their parent. The type of the newborn can even not be one of the types of the potential parents, which allows modelling mutations. Via a large population limit, we obtain a generalisation of 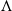 $\Lambda$
-Fleming–Viot processes, with a diffusion term and a general frequency-dependent selection, which allows for non-transitive interactions between the different types present in the population. We provide some properties of these processes related to extinction and fixation events, and give conditions for them to be realised as unique strong solutions of multidimensional stochastic differential equations with jumps. Finally, we illustrate the generality of our model with applications to some classical biological interactions. This framework provides a natural bridge between two of the most prominent modelling frameworks of biological evolution: population genetics and eco-evolutionary models.
$\Lambda$
-Fleming–Viot processes, with a diffusion term and a general frequency-dependent selection, which allows for non-transitive interactions between the different types present in the population. We provide some properties of these processes related to extinction and fixation events, and give conditions for them to be realised as unique strong solutions of multidimensional stochastic differential equations with jumps. Finally, we illustrate the generality of our model with applications to some classical biological interactions. This framework provides a natural bridge between two of the most prominent modelling frameworks of biological evolution: population genetics and eco-evolutionary models.
Keywords
MSC classification
- Type
- Research Papers
- Information
- Copyright
- © Applied Probability Trust 2020
References
- 4
- Cited by



