Article contents
On Fibonacci (or lagged Bienaymé-Galton-Watson) branching processes
Published online by Cambridge University Press: 14 July 2016
Abstract
This paper is concerned with a discrete-time population model in which a new individual entering the population at time t can produce offspring for the first time at time t + 2 and then subsequently at times t + 3, t + 4, ···. The numbers of offspring produced on each occasion are independent random variables each with the distribution of Z for which EZ = m <∞, and individuals have independent lines of descent. This model is contrasted with the corresponding Bienaymé-Galton-Watson one. If Xn denotes the number of individuals in the population at time n, it is shown that z–nXn almost surely converges to a random variable W, as n→∞, where 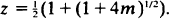 Various properties of W are obtained, in particular W > 0 a.s. if and only if EZ | log Z | < ∞ Results are also given on the rate of convergence of
Various properties of W are obtained, in particular W > 0 a.s. if and only if EZ | log Z | < ∞ Results are also given on the rate of convergence of 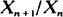 to z when Var Z < ∞ and these display a surprising dependence on the size of z.
to z when Var Z < ∞ and these display a surprising dependence on the size of z.
Keywords
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust
References
- 7
- Cited by


