Published online by Cambridge University Press: 09 December 2022
This article describes the limiting distribution of the extremes of observations that arrive in clusters. We start by studying the tail behaviour of an individual cluster, and then we apply the developed theory to determine the limiting distribution of
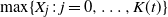 $\max\{X_j\,:\, j=0,\ldots, K(t)\}$
, where K(t) is the number of independent and identically distributed observations
$\max\{X_j\,:\, j=0,\ldots, K(t)\}$
, where K(t) is the number of independent and identically distributed observations
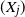 $(X_j)$
arriving up to the time t according to a general marked renewal cluster process. The results are illustrated in the context of some commonly used Poisson cluster models such as the marked Hawkes process.
$(X_j)$
arriving up to the time t according to a general marked renewal cluster process. The results are illustrated in the context of some commonly used Poisson cluster models such as the marked Hawkes process.