Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T05:11:12.815Z Has data issue: false hasContentIssue false
  • English
  • Français

On dams with Markovian inputs

Published online by Cambridge University Press:  14 July 2016

A. G. Pakes
A. G. Pakes*
Affiliation:
Monash University
Get access Rights & Permissions [Opens in a new window]

Abstract

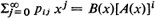Some recent work on discrete time dam models has been concerned with special cases in which the input process is a Markov chain whose transition probabilities, pij, are given by where A(·) and B(·) are probability generating functions (p.g.f.'s). In this paper we obtain some results for the general situation. The convergence norm of the matrix [pijxj] is found and the results are used to obtain the p.g.f. of the first emptiness time. Distributions of the dam content are obtained and conditions are found for the existence of their limits. The p.g.f. of this distribution is so complicated that its identification in any special case is extremely difficult, or even impossible. Thus useful approximations are needed; we obtain a ‘heavy traffic’ limit theorem which suggests that under certain circumstances the limiting distribution can be approximated by an exponential distribution.

Keywords

DAMSMARKOVIAN INPUTSBRANCHING PROCESSES
Type
Research Papers
Information
Journal of Applied Probability , Volume 10 , Issue 2 , June 1973 , pp. 317 - 329
Copyright
Copyright © Applied Probability Trust 1973 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ali Khan, M. S. and Gani, J. (1968) Infinite dams with inputs forming a Markov chain. J. Appl. Prob. 5, 72–83.CrossRefGoogle Scholar
Brockwell, P. J. and Gani, J. (1970) A population process with Markovian progenies. J. Math. Anal. Appl. 32, 264–273.Google Scholar
Dwass, M. (1968) A theorem about infinitely divisible distributions. Zeit. Wahrscheinlichkeitsth. 9, 287–289.Google Scholar
Feller, W. (1971) An Introduction to Probability Theory and its Applications. Vol. 2, 2nd. Ed. Wiley, New York.Google Scholar
Pakes, A. G. (1971a) Branching processes with immigration. J. Appl. Prob. 8, 32–42.CrossRefGoogle Scholar
Pakes, A. G. (1971b) Some limit the oremsfor the total progeny of a branchin gprocess. Adv. Appl. Prob. 3, 176–192.Google Scholar
Pakes, A. G. (1971c) On the critical Galton-Watson process with immigration. J. Austral. Math. Soc. 12, 476–482.Google Scholar
Pakes, A. G. (1971d) On a theorem of Quine and Seneta for the Galton-Watson process with immigration. Austral. J. Statist. 13, 159–164.Google Scholar
Pakes, A. G. (1972) Further results on the critical Galton-Watson process with immigration. J. Austral. Math. Soc. 13, 277–290.Google Scholar
Phatarfod, R. M. (1971) Some approximate results in renewal and dam theories. J. Austral. Math. Soc. 12, 425–432.Google Scholar
Phatarfod, R. M. and Mardia, K. V. (1973) Some results for dams with Markovian inputs. J. Appl. Prob. 10, 166–180.CrossRefGoogle Scholar
Seneta, E. (1969) Functional equations and the Galton-Watson process. Adv. Appl. Prob. 1, 1–42.Google Scholar
Vere-Jones, D. (1967) Ergodic properties of non-negative matrices, I. Pacific J. Math. 22, 361–386.CrossRefGoogle Scholar