Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bhattacharyya, Dhrubasish
Khan, Ruhul Ali
and
Mitra, Murari
2021.
Two-sample nonparametric test for comparing mean time to failure functions in age replacement.
Journal of Statistical Planning and Inference,
Vol. 212,
Issue. ,
p.
34.
Khan, Ruhul Ali
Bhattacharyya, Dhrubasish
and
Mitra, Murari
2021.
Exact and asymptotic tests of exponentiality against nonmonotonic mean time to failure type alternatives.
Statistical Papers,
Vol. 62,
Issue. 6,
p.
3015.
Bhattacharyya, Dhrubasish
Ali Khan, Ruhul
and
Mitra, Murari
2021.
A goodness of fit test for mean time to failure function in age replacement.
Journal of Statistical Computation and Simulation,
Vol. 91,
Issue. 17,
p.
3637.
Mitra, Murari
and
Khan, Ruhul Ali
2021.
Applied Advanced Analytics.
p.
19.
Khan, Ruhul Ali
Bhattacharyya, Dhrubasish
and
Mitra, Murari
2021.
On some properties of the mean inactivity time function.
Statistics & Probability Letters,
Vol. 170,
Issue. ,
p.
108993.
Fang, Zhigeng
Zhang, Qin
Cai, Jiajia
and
Liu, Sifeng
2022.
Optimal age replacement policies with multiple missions for multi-state systems.
Computers & Industrial Engineering,
Vol. 163,
Issue. ,
p.
107777.
Kayid, Mohamed
and
Alrasheedi, Adel
2022.
Weighted proportional mean inactivity time model.
AIMS Mathematics,
Vol. 7,
Issue. 3,
p.
4038.
Khan, Ruhul Ali
Bhattacharyya, Dhrubasish
and
Mitra, Murari
2023.
On some properties of distributions possessing a bathtub-shaped failure rate average.
Journal of Applied Probability,
Vol. 60,
Issue. 2,
p.
693.
Bhattacharyya, Dhrubasish
Khan, Ruhul Ali
and
Mitra, Murari
2023.
A new family of tests for DMTTF alternatives under complete and censored samples.
Communications in Statistics - Simulation and Computation,
Vol. 52,
Issue. 10,
p.
4603.
Mathew, Deemat C.
Alex, Reeba Mary
and
Kattumannil, Sudheesh K.
2024.
Jackknife empirical likelihood ratio test for testing mean time to failure order.
Statistical Papers,
Vol. 65,
Issue. 1,
p.
79.
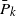 $\bar{P}_k$ of surviving the first k shocks are assumed to have discrete DMTTF, IMTTF and IDMTTF properties. The cumulative damage model of A-Hameed and Proschan [1] is studied in this context and analogous results are established. Weak convergence and moment convergence issues within the IDMTTF class of life distributions are explored. The preservation of the IDMTTF property under some basic reliability operations is also investigated. Finally we show that the intersection of IDMRL and IDMTTF classes contains the BFR family and establish results outlining the positions of various non-monotonic ageing classes in the hierarchy.
$\bar{P}_k$ of surviving the first k shocks are assumed to have discrete DMTTF, IMTTF and IDMTTF properties. The cumulative damage model of A-Hameed and Proschan [1] is studied in this context and analogous results are established. Weak convergence and moment convergence issues within the IDMTTF class of life distributions are explored. The preservation of the IDMTTF property under some basic reliability operations is also investigated. Finally we show that the intersection of IDMRL and IDMTTF classes contains the BFR family and establish results outlining the positions of various non-monotonic ageing classes in the hierarchy.