Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hall, Peter
1978.
Representations and limit theorems for extreme value distributions.
Journal of Applied Probability,
Vol. 15,
Issue. 3,
p.
639.
Kesten, Harry
1979.
The speed of convergence of a martingale.
Israel Journal of Mathematics,
Vol. 32,
Issue. 1,
p.
83.
1980.
Martingale Limit Theory and its Application.
p.
285.
Hall, Peter
1982.
On Some Simple Estimates of an Exponent of Regular Variation.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 44,
Issue. 1,
p.
37.
Scott, D.J.
and
Huggins, R.M.
1983.
On the embedding of processes in Brownian motion and the law of the iterated logarithm for reverse martingales.
Bulletin of the Australian Mathematical Society,
Vol. 27,
Issue. 3,
p.
443.
Clark, J. M. C.
1984.
Stochastic Differential Systems Filtering and Control.
Vol. 69,
Issue. ,
p.
129.
Huggins, R. M.
1985.
On functional laws of the iterated logarithm.
Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 69,
Issue. 2,
p.
243.
Huggins, R. M.
1985.
A strong invariance principle for reverse martingales.
Acta Mathematica Hungarica,
Vol. 46,
Issue. 1-2,
p.
93.
Clark, J. M. C.
and
Föllmer, H.
1987.
Stochastic Differential Systems.
Vol. 96,
Issue. ,
p.
331.
Clark, J. M. C.
1987.
Convergent martingales of asymptotically minimal fluctuation.
Probability Theory and Related Fields,
Vol. 75,
Issue. 4,
p.
531.
Pakes, Anthony G.
1992.
Divergence rates for explosive birth processes.
Stochastic Processes and their Applications,
Vol. 41,
Issue. 1,
p.
91.
Krasulina, T. P.
1996.
An estimate for the convergence rate of the robbins-monro process.
Journal of Mathematical Sciences,
Vol. 81,
Issue. 1,
p.
2430.
Kotz, Samuel
and
Balakrishnan, N.
1997.
Advances in Combinatorial Methods and Applications to Probability and Statistics.
p.
203.
Rosalsky, Andrew
and
Rosenblatt, Joseph
1997.
On the rate of convergence of series of banach space valued random elements.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 30,
Issue. 7,
p.
4237.
Rosalsky, Andrew
and
Rosenblatt, Joseph
1998.
On convergence of series of random variables with applications to martingale convergence and to convergence of series with orthogonal summands.
Stochastic Analysis and Applications,
Vol. 16,
Issue. 3,
p.
553.
Nam, Eunwoo
Rosalsky, Andrew
and
Volodin, Andrej I.
1999.
On convergence of series of independent random elements in banach spaces.
Stochastic Analysis and Applications,
Vol. 17,
Issue. 1,
p.
85.
Basak, Gopal K.
and
Dasgupta, Amites
2006.
Central and Functional Central Limit Theorems for a Class of Urn Models.
Journal of Theoretical Probability,
Vol. 19,
Issue. 3,
p.
741.
Rosalsky, Andrew
2007.
On the limiting behavior of tail series.
Journal of Statistical Planning and Inference,
Vol. 137,
Issue. 3,
p.
935.
Heyde, C. C.
2010.
Selected Works of C.C. Heyde.
p.
339.
Egloff, Daniel
and
Leippold, Markus
2010.
Quantile estimation with adaptive importance sampling.
The Annals of Statistics,
Vol. 38,
Issue. 2,


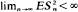 so that
so that 