Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Keiding, Niels
and
Nielsen, John E.
1975.
Branching processes with varying and random geometric offspring distributions.
Journal of Applied Probability,
Vol. 12,
Issue. 1,
p.
135.
Keiding, Niels
and
Nielsen, John E.
1975.
Branching processes with varying and random geometric offspring distributions.
Journal of Applied Probability,
Vol. 12,
Issue. 1,
p.
135.
Torrez, William C.
1979.
Calculating extinction probabilities for the birth and death chain in a random environment.
Journal of Applied Probability,
Vol. 16,
Issue. 04,
p.
709.
Bourgin, Richard D.
and
Cogburn, Robert
1981.
On determining absorption probabilities for Markov chains in random environments.
Advances in Applied Probability,
Vol. 13,
Issue. 2,
p.
369.
Vatutin, V. A.
and
Zubkov, A. M.
1993.
Branching processes. II.
Journal of Soviet Mathematics,
Vol. 67,
Issue. 6,
p.
3407.
Grey, D. R.
and
Zhunwei, Lu
1994.
The fractional linear probability generating function in the random environment branching process.
Journal of Applied Probability,
Vol. 31,
Issue. 1,
p.
38.
Jost, Jürgen
and
Wang, Ying
2014.
Optimization and Phenotype Allocation.
Bulletin of Mathematical Biology,
Vol. 76,
Issue. 1,
p.
184.


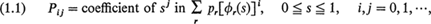
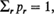 , and
, and 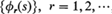 , is a corresponding sequence of probability generating functions. It is assumed that
, is a corresponding sequence of probability generating functions. It is assumed that 