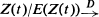If Z(t) denotes the population size in a Bellman-Harris age-dependent branching process such that a non-denenerate random variable W, then it is known that E(W) = 1 and that ϕ (u) = E(e–uW) satisfies a well-known integral equation. In this situation Athreya [1] has recently found a NASC for E(W |log W| y) <∞, for γ > 0. This paper generalizes Athreya's results in two directions. Firstly a more general class of branching processes is considered; secondly conditions are found for E(W 1 + βL(W)) < ∞ for 0 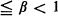β < 1, where L is one of a class of functions of slow variation.