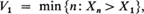Let X1,X2,X3,··· be independent, identically distributed random variables with a continuous distribution function and let the sequence of indices {Vr} be defined as follows: and for r ≧ 1, 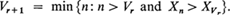Vr is the trial on which the rth (upper) record observation occurs. {Vr} will be an infinite sequence of random variables since the underlying distribution function of the X's is continuous. It is well known that the expected value of Vr. is infinite for every r (see, for example, Feller [1], page 15). Also define 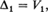and for r > 1 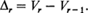δr is the number of trials between the (r - l)th and the rth record. The distributions of the random variables Vr and δr do not depend on the distribution of the original random variables. It can be shown (see Neuts [2], page 206 or Tata 1[4], page 26) that 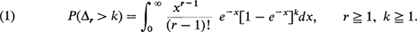The following theorem is due to Neuts [2].